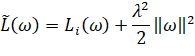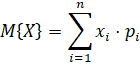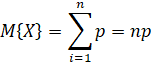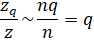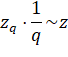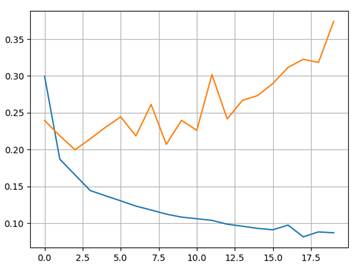
|
L2-регуляризатор и DropoutМы подошли к моменту, когда нужно подробнее познакомиться со способами борьбы с переобучением НС® Как мы говорили в курсе по машинному обучению (МО©, каждая модель немного переобучается. Наша задача, чтобы степень переобучения была как можно меньше. Те, кто проходил курс по МО¬ уже знакомы с двумя техниками борьбы с переобучением: регуляризация настраиваемых параметров и понижение размерности признакового пространства: https://proproprogs.ru/ml/ml-l2-regulyarizator-matematicheskoe-obosnovanie-i-primer-raboty При этом часто выделяют L1- и L2-регуляризации. Но при обучении НС¬ как правило, используют L2-регуляризацию весовых коэффициентов, так как L1-регуляризация склонна занулять некоторые веса и это может негативно сказаться на качестве работы НС® Помимо регуляризаторов специально для НС были предложены еще две довольно популярные техники борьбы с переобучением: Dropout и BatchNormalization. Но начнем с классической L2-регуляризации. Добавление L2-регуляризации для подбираемых параметровДо сих пор при обучении НС мы не использовали регуляризаторы и это не лучшая практика, так как нейросети склонны к переобучению. Это связано с огромным количеством настраиваемых параметров и заметно меньшим числом признаков. Вот пример графиков изменения средних значений функции потерь, по эпохам, для обучающей и валидационной выборок без L2-регуляризации весовых коэффициентов:
Чтобы добавить L2-регуляризатор, в выбранном оптимизаторе достаточно прописать параметр weight_decay, например, так: optimizer = optim.Adam(params=model.parameters(), lr=0.01, weight_decay=0.001) Здесь величина weight_decay=0.001 является аналогом коэффициента λ в формуле функции потерь:
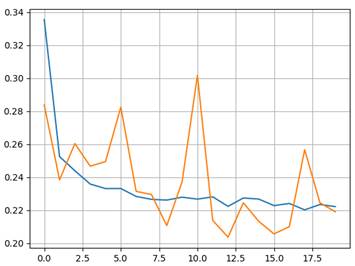
Аналогом, но не точным соответствием, т.к. оптимизаторы фреймворка PyTorch каждый по-своему применяют параметр weight_decay. Но одно можно сказать определенно. Если weight_decay не равен нулю, то при обучении будет применяться L2-регуляризатор. Само же значение weight_decay мы выбираем сами в зависимости от типа задач. Обычно оно берется в диапазоне [0.001; 0.00001]. Но это не строго. После добавления L2-регуляризатора характер графиков заметно меняется:
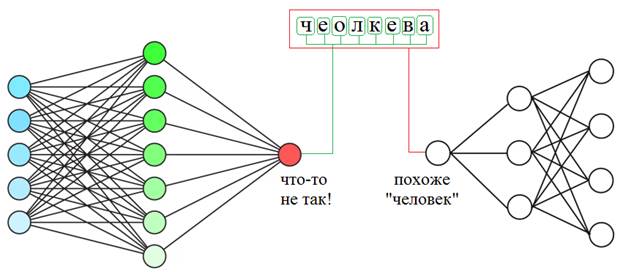
Уже нет явного расхождения и можно ожидать лучших обобщающих свойств полученной НС® Идея алгоритма DropoutВообще эффект переобучения можно описывать разными примерами с разных точек зрения. Для лучшего понимания приведу еще один. Предположим, что мы читаем текст. Мозг среднестатистического человека устроен так, что мы хорошо воспринимаем слова, даже если буквы в них написаны не по порядку (кроме первой и последней):
Так вот, если НС из-за большого числа нейронов подстроится под каждую букву слова, то этот текст для нее будет совершенно нечитаемым. Но сеть с небольшим числом нейронов, которая воспринимает слово в целом, сохранит способность к обобщению и правильному распознаванию.
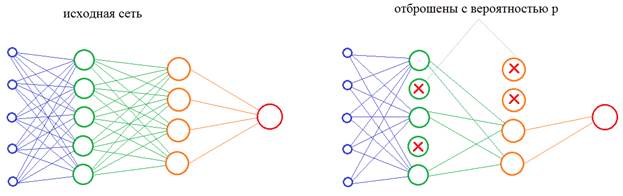
Но это не всегда дает желаемые результаты. Не редко с уменьшением числа нейронов уменьшается и точность выходных значений, то есть, показатель качества работы нейросети ухудшается. Поэтому было бы хорошо с одной стороны сохранить заданное число нейронов, а с другой постараться уменьшить их специализацию, т.е. увеличить обобщающую способность. Как раз для этого и был предложен алгоритм Dropout. На русский язык его иногда переводят как «метод прореживания» или «метод исключения», но чаще так и говорят - «дропаут». Этот метод исходит из того, что корень проблемы переобучения кроется в излишней специализации каждого отдельного нейрона. Цель Dropout сделать из нейронов «специалистов более широкого профиля». Но как уменьшить специализацию, сохраняя прежнее их число? Очень просто. Давайте представим, что в некоторой школе работают учителя по различным предметам: химия, биология, история, математика, физика, география и информатика. Это их специализация. Затем, в какой-то момент директор школы озаботился их приверженностью только одной дисциплине и решил расширить горизонты их профессиональной деятельности. Что он сделал? Он заставил учителя по химии время от времени вести занятия по физике, учителя по физике – химию, математика менялась с информатикой, а биология, история и география – между собой. В итоге, учителям волей-неволей пришлось изучить смежные дисциплины и расширить свою специализацию. Теперь, директор школы был доволен и знал, если какой-либо отдельный учитель заболеет или уволится, у него будет кем его заменить.
Теперь, осталось понять, как проделать тот же фокус с нейронами в нейронной сети? Как в процессе обучения им «сказать», чтобы они брали на себя функции других нейронов? Решение просто до гениальности: на каждой итерации изменения весовых коэффициентов часть нейронов нужно исключать с заданной вероятностью p:
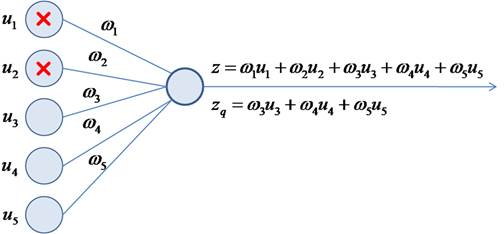
Это эквивалентно ситуации, когда часть учителей заболела и остальные вынуждены их заменять. Причем, в следующий момент, уже другие учителя уходят на больничный, а оставшиеся их заменяют. В результате, расширяется специализация всех учителей школы. Именно это происходит с нейронами в алгоритме dropout, которые то выключаются, то включаются. В какой же момент происходит их переключение? Как я выше отмечал – на каждой итерации изменения весов, то есть, при обработке каждого нового батча. Переключение нейронов происходит после каждой корректировки весовых коэффициентов. После того, как сеть обучена, включаются все нейроны и эффект переобучения (излишней специализации) должен заметно снизиться. Некоторые из вас здесь могут заметить одно важное несоответствие. Когда в процессе обучения с частью выключенных нейронов, мы пропускаем входной сигнал, то число входных связей на каждом нейроне уменьшается пропорционально вероятности p:
В режиме эксплуатации значение на входе нейрона будет z, а в момент обучения – значение:
Как вы понимаете, это приводит к искаженным входным значениям, а значит, и к неверным результатам на выходе всей НС® Как поправить ситуацию, чтобы, в среднем, эти суммы были равны? Для этого нужно вычислить среднее число выключенных нейронов в текущем слое. Учитывая, что понятие среднего в теории вероятностей – это математическое ожидание, которое, в дискретном случае, можно записать в виде:
Здесь роль случайной
величины X играет число
исключенных нейронов в текущем слое;
Соответственно, останется, в среднем:
нейронов. Где q – вероятность того, что нейрон останется (не будет исключен). Отсюда получаем, что средний суммарный сигнал на входах нейронов следующего слоя будет меньше на величину:
Из этого выражения хорошо видно, что для сохранения масштаба суммы, ее нужно разделить на величину q:
Во многих фреймворках алгоритм Dropout реализован именно так: суммарный сигнал на входах нейронов масштабируется, эмулируя поведение полной сети со всеми нейронами. Благодаря этому, в среднем, выходной сигнал сети соответствует истинным значениям и при ее эксплуатации (со всеми включенными нейронами) не будет возникать никаких «сюрпризов». Кстати, это одна из причин, почему во фреймворке PyTorch модели работают в двух режимах:
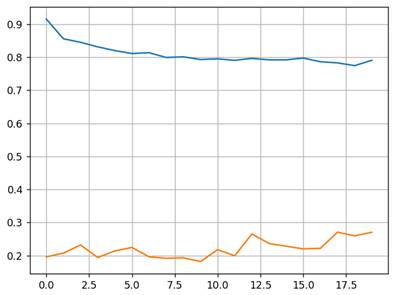
В описанной схеме остается один важный вопрос: как выбрать значение вероятности p? Авторы этого подхода рекомендуют для нейронов скрытого слоя начинать со значения p=0,5. А затем, при необходимости, попробовать чуть большие и чуть меньшие величины. То есть, этот параметр подбирается, исходя из опыта и некоторого здравого смысла. Также следует иметь в виду, что Dropout может, как помочь, так и ухудшить конечный результат. Если положительного эффекта не наблюдается, то от этого подхода лучше отказаться и попробовать другие методы борьбы с переобучением. Причем, изначально в сеть добавлять Dropout не следует. Только если явно наблюдается подстройка модели под обучающую выборку, можно прибегнуть к этому подходу, как к одному из возможных вариантов. Реализация Dropout в PyTorchДавайте добавим Dropout после первого слоя НС распознавания рукописных цифр. Для этого в класс DigitNN достаточно добавить две строчки: class DigitNN(nn.Module): def __init__(self, input_dim, num_hidden, output_dim): super().__init__() self.layer1 = nn.Linear(input_dim, num_hidden) self.layer2 = nn.Linear(num_hidden, output_dim) self.dropout_1 = nn.Dropout1d(0.3) def forward(self, x): x = self.layer1(x) x = nn.functional.relu(x) x = self.dropout_1(x) x = self.layer2(x) return x Команда nn.Dropout1d(0.3) создает объект Dropout для обработки батчей из одномерных тензоров с вероятностью p=0,3 отключения нейронов сети. Именно в таком виде тензоры передаются от слоя к слою в нашей НС® Забегая вперед отмечу, что класс Dropout2d способен применять алгоритм дропаут к двумерным тензорам. Но, что это за двумерные тензоры и откуда они берутся, мы с вами будем говорить на будущих занятиях, когда речь пойдет о сверточных НС® После создания объекта nn.Dropout1d(0.3) в методе forward пропускаем выходные значения нейронов первого слоя через слой Dropout, в котором имитируется работа отключения части нейронов при каждом новом батче. Обратите внимание, что слой Dropout обычно прописывают после функции активации. Хотя, формально никто не мешает записать его и перед ней. В ряде случаев это может давать даже лучшие результаты. Пусть модель содержит избыточное число нейронов скрытого слоя: model = DigitNN(28 * 28, 128, 10) И уберем в оптимизаторе L2-регуляризацию: optimizer = optim.Adam(params=model.parameters(), lr=0.01) Оценим работу слоя Dropout при обучении такой НС® После 20 эпох получим следующие графики для обучающей и валидационной выборок:
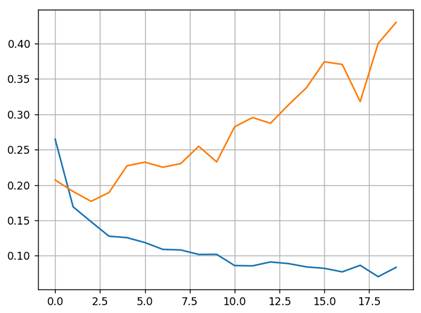
А вот какой вид принимают те же графики без слоя Dropout:
Налицо эффект переобучения. И, как видим, алгоритм Dropout действительно не дает расходиться показателям обучающей и валидационной выборок, а значит, снижается вероятность переобучения модели. На практике, как правило, при обучении НС всегда применяют L2-регуляризацию для оптимизируемых параметров: optimizer = optim.Adam(params=model.parameters(), lr=0.01, weight_decay=0.001) А слой Dropout только по необходимости. Видео по теме |
- вероятность
выключения; 
- число
нейронов, к которым применяется эта вероятность; n - общее число
нейронов в слое. Получаем среднее значение числа исключенных нейронов:
