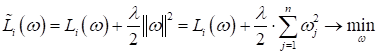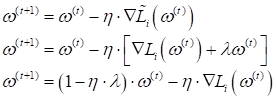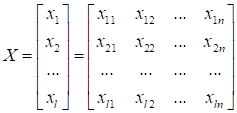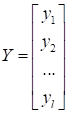|
L2-регуляризатор. Математическое обоснование и пример работыПрактический курс по ML: https://stepik.org/course/209247/ Давайте вернемся снова к вопросу переобучения моделей. Я напомню, что ранее мы с вами говорили, что модели могут переобучаться и знаем, как это можно оценить с помощью отложенной выборки или методом кросс-валидации или какими-либо другими подобными способами.
Однако, если переобучение все же произошло, то что делать для уменьшения этого эффекта? Конечно, вы сейчас можете сказать, что нужно уменьшить сложность модели, то есть, сократить размер признакового пространства. Да, если это возможно, то можно попробовать такой вариант. Но не всегда мы можем взять и самовольно отбросить часть признаков. Поэтому хотелось бы решить проблему с переобучением, не меняя размера признакового пространства. Давайте посмотрим, как это обычно делают в задачах машинного обучения. Вначале проведем небольшое исследование. Для функции
вычислим коэффициенты полинома, опираясь только на четные отсчеты (с нулевого и через один). Это легко сделать в программе на Python с использованием пакета Numpy: import numpy as np x = np.arange(0, 10.1, 0.1) y = 1/(1+10*np.square(x)) x_train, y_train = x[::2], y[::2] z_train = np.polyfit(x_train, y_train, 3) print(z_train) Если вы не
знаете Python, то никаких
проблем. Главный математический вывод я сейчас поясню. Смотрите, вначале мы
берем для x диапазон от 0
до 10.1 с шагом 0,1. Далее, формируем список значений функции Вот что получается при увеличении числа коэффициентов (степени полинома):
Начальные коэффициенты принимают малые значения, а последние резко возрастают. То есть, с увеличением сложности модели растет и диспропорция в коэффициентах. Конечно, это чисто эмпирическое замечание. Но оно имеет некоторое математическое обоснование. Об этом я расскажу позже. А вначале давайте также «в лоб» решим эту проблему, следующей эвристикой. В функцию потерь добавим еще одно слагаемое:
То есть, теперь
мы будем искать минимум не только самой (прежней) функции потерь Причем, обратите
внимание, мы сюда не включаем первый нулевой весовой коэффициент
Если мы здесь
наложим ограничения на большие значения Отлично, это я
думаю, понятно. Теперь разберем, почему множитель записан как
Видите, какая
получилась аккуратная формула производной? В этом удобство коэффициента
Последнее
выражение показывает, чем отличается градиентный спуск при новой
(модифицированной) функции потерь. На каждой итерации вектор коэффициентов
уменьшается на величину Такой подход получил название L2-регуляризация или гребневая регрессия (в машинном обучении используют первое название). Хорошо, мы придумали некоторую эвристику для предотвращения переобучения модели и позже посмотрим, как она работает. А сейчас попробуем понять, какие же соображения стоят за выбором такого регуляризатора? Я начну с того, что в задачах регрессии не редко используют квадратичную функцию потерь вида:
а модель часто выбирают линейной:
В итоге модифицированная функция потерь в векторной записи, примет вид:
Тогда эмпирический риск (функционал качества) для всей обучающей выборки можно записать в векторно-матричной форме как:
где
Тогда
оптимальный вектор коэффициентов
где Из этой
последней формулы хорошо видно, какую роль играет L2-регуляризация
при квадратической функции потерь. Большой разброс в значениях вектора
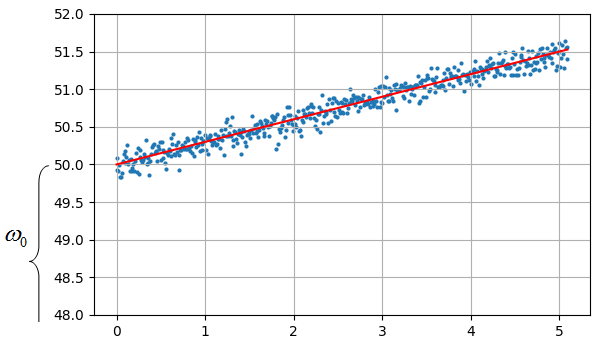
коэффициентов Простой пример. Пусть изначально ширина и длина жуков (гусениц и божьих коровок) измеряется в мм:
А, затем, мы добавляем еще два признака – измерения длины и ширины в см:
Очевидно, признаки width_mm, width_cm и height_mm, height_cm будут попарно линейно-зависимыми, то есть, один может быть получен из другого простым умножением на число. В этом случае мы будем получать разброс в значениях вектора весовых коэффициентов (при использовании градиентных алгоритмов) и, как следствие, переобученность модели. Вторая важная
причина, приводящая к эффекту переобучения, число наблюдений меньше числа
признаков Но, после того,
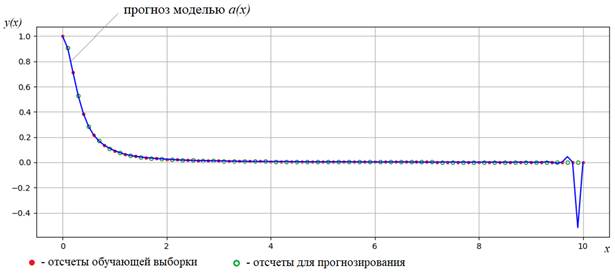
как мы добавили L2-регуляризатор, к диагональным элементам матрицы Вот так, математически, можно объяснить смысл L2-регуляризатора при квадратичной функции потерь. Конечно, здесь сразу возникает вопрос, а как его можно интерпретировать при других, не квадратичных функциях? В этих случаях он становится просто эвристикой, которая хорошо себя зарекомендовала на практике. Модели с L2-регуляризатором действительно обладают лучшими обобщающими способностями и, например, при обучении нейронных сетей используются практически повсеместно. Давайте посмотрим, как работает модель без L2-регуляризатора и с L2-регуляризатором на примере аппроксимации полиномиальной функции:
Программу можно скачать по ссылке: machine_learning_11_overfittin.py Если взять модель с размерностью признакового пространства n = 12, то есть, модель представляется полиномом степени n-1:
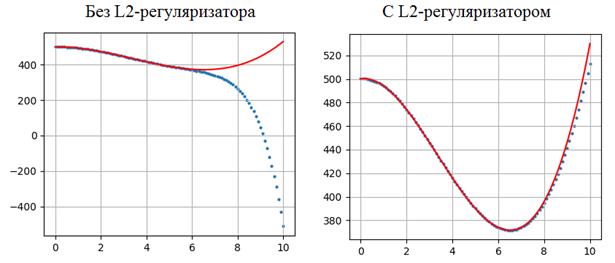
то результат обучения будет, следующий:
Как видите, регуляризация значительно улучшает обобщающие свойства модели, сохраняя общее число коэффициентов (размер признакового пространства). В результате, мы заметно уменьшили степень переобучения всего лишь за счет добавления квадрата весов в функцию потерь. Практический курс по ML: https://stepik.org/course/209247/ Видео по теме |
. После этого
отбираем отсчеты с шагом 2 (через один) из массивов x и y. Получаем
тренировочный набор данных. Затем, с помощью функции polyfit() пакета Numpy вычисляем
коэффициенты полинома по тренировочному набору. В конце выводим полученные
значения в консоль.
,
но и требовать при этом минимум суммы квадратов весов. А параметр 
-
это степень учета этой суммы, то есть, насколько сильно мы хотим обращать
внимание на большие значения в весовых коэффициентах при минимизации новой
функции потерь 
.
,
который отвечает за сдвиг гиперплоскости. Это единственный коэффициент, который
может принимать любые значения. Почему это важно? Смотрите, когда мы решаем,
например, задачу регрессии, то множество точек может исходить не из нуля, а
иметь некоторое смещение. И в реальных задачах это смещение может быть сколь
угодно большим:
,
то не сможем построить адекватную модель для описания этого множества точек.
Тот же эффект наблюдается и в задачах классификации, когда образы в признаковом
пространстве могут быть смещены относительно нуля. Здесь также первый параметр 
,
да и веса возводятся в квадрат, а не берутся, например, по модулю? Забегая
вперед, скажу, что и модули тоже используют. А вот множитель 
,
устремляя его к нулю, но не достигая нуля (экспоненциальное затухание). А
степень сокращения коэффициентов, как раз настраивается параметром 
.
-
входные векторы обучающей выборки; 
-
вектор (или матрица) целевых значений обучающей выборки:
легко
найти чисто математически, дифференцируя эмпирический риск по вектору 
и
приравнивая результат нулю, получим:
,
-
единичная матрица.
является
плохо обусловленной, то есть, некоторые (или все) признаки, из которых
составлены векторы 
обучающей
выборки практически линейно-зависимы.
.
Тогда матрица 
