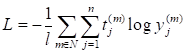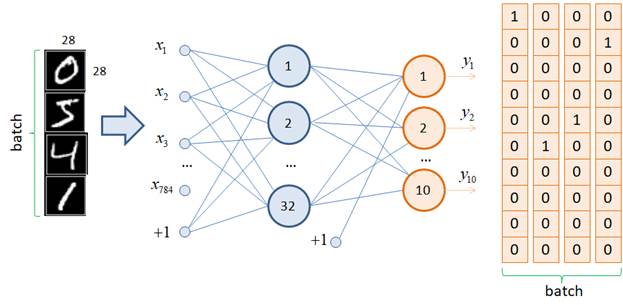
Классификация изображений цифр БД MNIST

Смотреть материал на YouTube | RuTube

На прошлом занятии мы с вами научились работать с выборкой изображений цифр, хранящихся в каталогах определенной структуры. Следующим шагом сформируем и обучим нейронную сеть правильно классифицировать эти изображения. Для этого нужно определиться со структурой НС. Строгого ответа, как это сделать, нет, т.к. структура выбирается самим разработчиком исходя из его опыта и представлений о решении конкретной задачи. Общий ориентир здесь такой: для распознавания графических образов хорошо себя зарекомендовали сверточные НС. Но мы о них пока еще ничего не знаем, поэтому воспользуемся обычной полносвязной НС следующего вида:

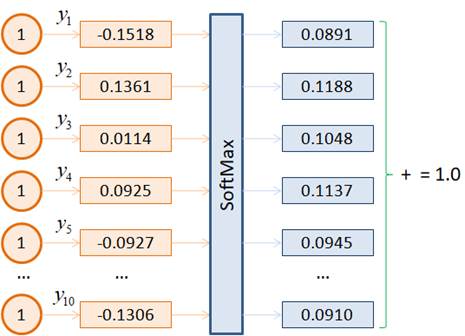
На вход здесь подаются тензоры размерностью 784 элементов, затем, сигнал проходит через один скрытый слой из 32 нейронов, а на последнем выходном слое из 10 нейронов формируется выходной тензор размерностью в 10 элементов – по одному на каждый класс цифр.

В качестве функций активации скрытого слоя выберем популярную на сегодняшний день ReLU, а выходные значения сети оставим без изменения, как есть. Это эквивалентно применению линейной функции активации.

По идее, решая задачу многоклассовой классификации, на выходе часто применяют функцию softmax, которая преобразует выходной сигнал в эквивалент вероятностей принадлежности входного изображения тому или иному классу:

При этом сумма всех значений становится равной 1.0. Однако, как вероятности эти величины воспринимать не следует, к фактической вероятности принадлежности к тому или иному классу они не имеют прямого отношения. По сути, функция активации выходного слоя часто служит лишь для преобразования выходных значений НС в желаемый для нас формат восприятия.

Почему же мы в нашей НС не прописываем функцию softmax? Дело в том, что для обучения сети будет использоваться функция потерь:

loss_function = nn.CrossEntropyLoss()

которая хорошо подходит для многоклассовой классификации. И согласно документации, этой функции следует передавать выходные значения сети, без применения какой-либо нелинейной функции активации. Функция CrossEntropyLoss сама применит необходимые преобразования к переданным значениям и вычислит итоговые потери. Это рекомендуемая практика, которая часто повышает скорость и качество обучения НС. Это же касается и многих других встроенных функций потерь фреймворка PyTorch. Им также следует передавать истинные (не искаженные) выходные значения сети. Если же потом после обучения в процессе эксплуатации потребуется другой формат выходных значений, то всегда их можно будет преобразовать любой выбранной нелинейной функцией.

Учитывая указанные замечания, класс нейронной сети можно определить следующим образом:

class DigitNN(nn.Module):
    def __init__(self, input_dim, num_hidden, output_dim):
        super().__init__()
        self.layer1 = nn.Linear(input_dim, num_hidden)
        self.layer2 = nn.Linear(num_hidden, output_dim)
 
    def forward(self, x):
        x = self.layer1(x)
        x = nn.functional.relu(x)
        x = self.layer2(x)
        return x

После этого создадим объект НС с помощью команды:

model = DigitNN(28 * 28, 32, 10)

Здесь 28*28 = 784 – размер входных данных (пикселей изображения 28x28); 32 – число нейронов скрытого слоя (подбираемый параметр разработчиком НС); 10 – число выходных нейронов (для формирования меток 10 классов).

При обучении этой НС будем использовать оптимизатор Adam:

optimizer = optim.Adam(params=model.parameters(), lr=0.01)

и кросс-энтропию в качестве функции потерь:

loss_function = nn.CrossEntropyLoss()

Как показала практика, эта функция хорошо подходит при обучении НС в задачах многоклассовой классификации. Формально она описывается выражением:

где – размер обучающей выборки; - требуемые выходы для m-го входного вектора и j-го выхода сети; - целевое значение j-го выхода.

Далее определим переменную с количеством эпох обучения и переведем модель в тренировочный режим:

epoch = 2
model.train()

Теперь все готово, чтобы записать главный цикл обучения следующим образом:

for _e in range(epoch):
    for x_train, y_train in train_data:
        predict = model(x_train)
        loss = loss_function(predict, y_train)
 
        optimizer.zero_grad()
        loss.backward()
        optimizer.step()

После обучения НС переведем ее в режим эксплуатации и вычислим долю верных классификаций (метрику accuracy) по тестовой выборке:

d_test = DigitDataset("dataset", train=False, transform=to_tensor)
test_data = data.DataLoader(d_test, batch_size=500, shuffle=False)
 
Q = 0
 
# тестирование обученной НС
model.eval()
 
for x_test, y_test in test_data:
    with torch.no_grad():
        p = model(x_test)
        p = torch.argmax(p, dim=1)
        y = torch.argmax(y_test, dim=1)
        Q += torch.sum(p == y).item()
 
Q /= len(d_test)
print(Q)

Здесь мы на каждой итерации выбираем по 500 образов из тестовой выборки без перемешивания, т.к. при тестировании это не имеет никакого значения, а затем, применяем функцию torch.argmax к полученным выходным значениям НС. Эта функция возвращает индекс элемента тензора p с наибольшим значением по второй оси (dim=1). В результате получаем пакет данных с метками классов, прогнозируемых НС, в виде чисел от 0 до 9. Ту же самую операцию выполняем и для целевого тензора y_test. Следующей командой подсчитываем число совпадающих меток с целевыми значениями.

После запуска программы получается чуть более 90% правильных классификаций. Это неплохой результат для такой простой НС.

Модуль tqdm

Как видим, процесс обучения полученной НС может протекать продолжительное время. Поэтому хотелось бы видеть прогресс обучения, чтобы понимать, сколько прошло и сколько еще осталось до конца. Для этого нередко используют довольно удобную библиотеку tqdm. Давайте ей воспользуемся.

Вначале установим ее командой (в терминале):

pip install tqdm

А затем, импортируем в программе класс tqdm:

from tqdm import tqdm

После этого вначале каждой эпохи будем создавать объект этого класса и выполнять итерирование во вложенном цикле уже по нему:

for _e in range(epoch):
    train_tqdm = tqdm(train_data, leave=True)
    for x_train, y_train in train_tqdm:
       ...

Второй аргумент leave=True будет оставлять предыдущий progress bar на экране. В результате выполнения двух эпох увидим следующее отображение:

100%|██████████| 1875/1875 [01:40<00:00, 18.72it/s]
100%|██████████| 1875/1875 [00:20<00:00, 92.57it/s]
0.9437

Это уже намного лучше. Но еще не все. Дополнительно здесь можно выводить любую желаемую информацию по эпохам. Например, номер эпохи и значение функции потерь. Делается это следующим образом:

for _e in range(epoch):
    loss_mean = 0 # среднее значение функции потерь (по эпохе)
    lm_count = 0 # текущее количество слагаемых
 
    train_tqdm = tqdm(train_data, leave=True)
    for x_train, y_train in train_tqdm:
        predict = model(x_train)
        loss = loss_function(predict, y_train)
 
        optimizer.zero_grad()
        loss.backward()
        optimizer.step()
 
        lm_count += 1 # увеличиваем число слагаемых
        loss_mean = 1/lm_count * loss.item() + (1 - 1/lm_count) * loss_mean
        train_tqdm.set_description(f"Epoch [{_e+1}/{epoch}], loss_mean={loss_mean:.3f}")

Формула пересчета среднего арифметического значения рассматривалась на занятии по машинному обучению:

https://proproprogs.ru/ml/ml-stohasticheskiy-gradientnyy-spusk-sgd-i-algoritm-sag

То есть, вначале вычисляются все необходимые значения, а затем, с помощью метода set_description объекта train_tqdm выводится информация в виде сформированной строки вначале прогресс-бара. После запуска программы увидим:

Epoch [1/2], loss_mean=0.335: 47%|████▋ | 876/1875 [00:09<00:10, 92.40it/s]

Классификация изображений цифр БД MNIST

Модуль tqdm

Видео по теме