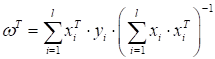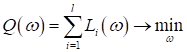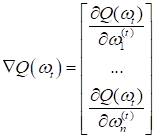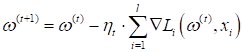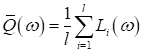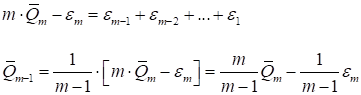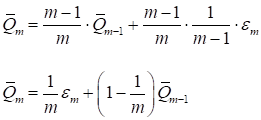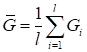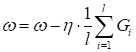|
Стохастический градиентный спуск SGD и алгоритм SAGНа предыдущем занятии мы с вами ввели гладкие функции потерь для решения задачи бинарной классификации. И увидели, что при квадратической функции решение можно найти по формуле:
Однако, далеко не всегда реальные задачи удается так элегантно и просто решить. Главные проблемы возникают из-за плохой обусловленности обратной матрицы (то есть, она может не существовать) и с очень большой размерностью пространства признаков. Например, в нейронных сетях размер вектора коэффициентов достигает 100 000, 1 000 000 и это еще не самые большие сети. Обращать такие огромные матрицы вычислительно очень сложно. Поэтому нужны другие, численные подходы к задаче оптимизации показателя качества (эмпирического риска):
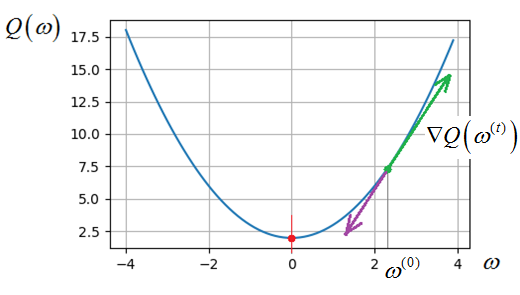
Для дифференцируемых функций самым простым и распространенным методом их оптимизации (поиска экстремума) являются градиентные алгоритмы. Идея градиентных алгоритмов очень проста. Если взять какую-либо дифференцируемую функцию с одной точкой минимума, например, параболу:
то можно постепенно
уточнять некоторое начальное значение коэффициента
(здесь t – номер шага).
Так как антиградиент показывает направление к ближайшей точке экстремума
функции, то при правильном подборе шага
Подробно о работе градиентных алгоритмов я уже рассказывал на одном из своих занятий, ссылка на него будет под этим видео: https://www.youtube.com/watch?v=OKeZEbJgQKc&list=PLA0M1Bcd0w8yZNgl5J814WQykTZnzj771&index=3 Поэтому я не буду здесь вдаваться в детали его классической реализации (там ничего сложного нет), а отмечу принцип его работы для вектора параметров
В этом случае мы имеем многомерную функцию и на каждой итерации нам нужно вычислять частные производные по каждому из значений:
Получим вектор из частных производных, которым, затем, уточним значение вектора коэффициентов на новой итерации:
То есть, общий принцип сохраняется, просто мы переходим в векторную форму описания градиентного алгоритма. Стохастический градиентный спуск (SGD)Если расписать эту формулу еще подробнее, то вместо градиента функционала у нас получится сумма градиентов функции потерь по обучающей выборке:
Получается,
чтобы сделать один шаг классического градиентного спуска, нам нужно вычислить
производные по функциям потерь для всех объектов
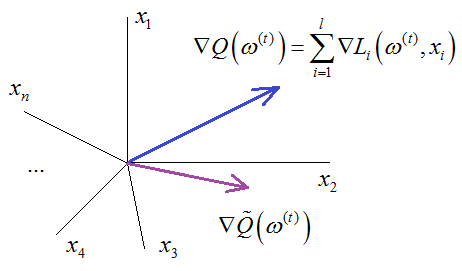
Здесь через Возникает вопрос, что нам взять в качестве псевдоградиента, то есть, как сократить объем вычислений для истинного градиента и при этом сохранить сходимость алгоритма к точке локального минимума? Самое простое и радикальное, что можно сделать, на каждом шаге из всей суммы брать только одно наблюдение (одно слагаемое) и по нему вычислять текущее приближение:
где Будет ли в этом случае наш псевдоградиент образовывать в среднем острый угол с истинным градиентом? Другими словами, будем ли мы в среднем двигаться в направлении локального минимума функционала качества? Да, можно показать, что по закону больших чисел, при большом числе шагов (приближений) этот псевдоградиент сходится к истинному градиенту. А, значит, рано или поздно мы достигнем с его помощью точки минимума. Эта идея положена в основу метода стохастического градиентного спуска (Stochastic Gradient Descent – SGD). Иногда его еще называют методом Роббинса-Монро. Алгоритм можно записать в виде следующего псевдокода:
1) инициализация
весов 2) начальное вычисление функционала качества:
3) цикл 4) случайный выбор
наблюдения 5) вычисление
функции потерь 6) шаг
псевдоградиентного алгоритма: 7) пересчет
функционала качества: 8) пока Здесь у вас
может вызвать недоумение формула пересчета среднего показателя качества Откуда взялась эта рекуррентная формула? Давайте представим, что мы вычисляем простое арифметическое среднее по m величинам:
Можно заметить, что
откуда
Вот формула
рекуррентного пересчета среднего арифметического при появлении нового
слагаемого
Если расписать эту формулу, то она будет эквивалентна следующей сумме:
Мы здесь видим
экспоненциально убывающие коэффициенты при
где N – интервал
сглаживания. Например, при N = 99 получаем Я думаю, что теперь вам должно быть все понятно в работе алгоритма стохастического градиента. Последнее, что здесь важно отметить, что существуют другие варианты вычисления псевдоградиента. Мы говорили, что достаточно брать по одному случайному наблюдению и вычислять текущее направление движения. Однако, в этом случае сходимость алгоритма будет напоминать броуновское движение (случайное блуждание). Чтобы как то сгладить этот тренд, можно брать не одно, а несколько наблюдений на каждой итерации, их суммировать и получать более точные направления движения. Это несколько увеличит объем вычислений, но в ряде задач дает лучшие результаты скорости сходимости, чем классический SGD с одним наблюдением. Например, так делается при обучении нейронных сетей, когда градиенты вычисляются по пакетам наблюдений (мини-батчам). Это тоже будет алгоритм SGD, но использующий группу входных данных из обучающей выборки для корректировки весовых коэффициентов. Алгоритм SAG (Stochastic Average Gradient)В заключение этого занятия я хочу рассказать об еще одной интересной реализации стохастического градиентного спуска, предложенной группой зарубежных ученых в 2013-м году. Я сразу приведу его псевдокод, т.к. он сильно похож на классический алгоритм SGD:
1) инициализация
весов 2) инициализация
всех градиентов
3) вычисление
среднего градиента по всей выборке: 4) начальное
вычисление функционала качества: 5) цикл 6)
случайный
выбор наблюдения 7)
вычисление
функции потерь 8)
вычисление градиента 9)
шаг псевдоградиентного алгоритма: 10)
пересчет
функционала качества: 11)
пока
Здесь красным отмечены строчки, которыми отличается алгоритм SAG от SGD. Смотрите, вначале мы вычисляем все градиенты для каждого наблюдения обучающей выборки. Затем, вычисляем их среднее арифметическое и далее в цикле уточняем веса, используя градиенты по всей выборке, а не по одному вектору, как это было в SGD. Но вы скажете, это же вычислительно очень сложно каждый раз считать сумму по всем объектам выборки? Верно, поэтому делать мы этого не будем. Здесь на каждой итерации также берется случайный вектор из тренировочной выборки и только для него вычисляется градиент. А, далее, мы обновляем сумму градиентов: вычитаем из нее прежнее k-е значение градиента и добавляем новое. Все. Эта процедура выполняется моментально и заново все считать не нужно. Правда платить за это приходится большим объемом памяти, в которой нужно хранить все значения градиентов для каждого объекта обучающей выборки. Но, современные компьютеры вполне могут себе это позволить. Даже при выборках в миллионы наблюдений. Поэтому данный алгоритм является весьма перспективным. Итак, из этого занятия вы должны понять, зачем вообще нужны градиентные алгоритмы, как реализуется стохастический градиентный спуск (SGD) и алгоритм SAG. Видео по теме |
,
перемещаясь в направлении антиградиента функции:
можно
достаточно точно найти точку минимума функции.
обучающей
выборки и сложить их. Представляете, какой здесь может получаться объем
вычислений, если наша выборка состоит из сотен тысяч, а то и миллионов векторов
обозначен
псевдоградиент.
-
псевдоградиент; k – случайный индекс вектора из обучающей выборки.
,
шаг сходимости 
,
скорость «забывания» 
.
.
из
и/или
.
Например, когда он достигает определенного значения, то процесс обучения можно
остановить. Но, формально, он вычисляется как среднее арифметическое от функций
потерь по всей выборке. А это снова большой объем вычислений, которого, как
раз, хотим избежать. Поэтому в алгоритмах SGD функционал 
.
Экспоненциальное скользящее среднее работает по тому же принципу, только вместо
изменяющегося шага 1/m берется постоянная величина лямбда:
.
Значение параметра 
,
.
