|
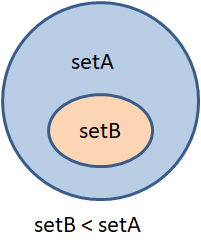
Множества (set). Операции над множествамиКурс по структурам данных: https://stepik.org/a/134212 На предыдущих занятиях мы с вами подробно познакомились с работой бинарного дерева. Его можно использовать, как самостоятельную структуру данных. Но также оно применяется в качестве основы других известных структур, например, упорядоченных множеств, о которых речь пойдет на этом занятии. Само по себе множество (set) – это коллекция данных, состоящая из уникальных значений. То есть, дубли в нем отсутствуют. Множества реализованы практически во всех высокоуровневых языках, в том числе Python и С++. Но множества в Python являются неупорядоченными коллекциями и сделаны на базе хэш-таблиц, о которых мы еще будем говорить. А вот в языке С++ имеются упорядоченные множества, которые определены в стандартной библиотеки шаблонов STL через класс set. Причем, в их основе лежат бинарные красно-черные деревья. На этом и следующих занятиях речь пойдет исключительно об упорядоченных множествах. Давайте вначале разберемся, почему применяются именно бинарные деревья? Во-первых, как мы помним, в вершинах дерева, как правило, хранятся уникальные значения. А это именно то, что требуется для множеств. Во-вторых, поиск некоторого значения в бинарном дереве выполняется за логарифмическое время (O(log n) операций). Благодаря этому, мы относительно быстро можем реализовать оператор проверки принадлежности какого-либо значения множеству: value in sНапример: 2 in s где s – некоторое множество. В-третьих, при обходе дерева в глубину по алгоритму LNR получаем упорядоченную по возрастанию последовательность данных. Разумеется, при этом данные в дереве должны добавляться по правилу: меньшие значения – в левое поддерево, большие – в правое. Благодаря простому получению упорядоченных значений элементов множества, мы можем относительно легко реализовать алгоритмы сравнения двух множеств между собой. При сравнении на равенство: setA == setBдостаточно проверить равенство числа элементов в множествах, выстроить значения по возрастанию и попарно их сравнить между собой. Если окажется, что множества содержат одинаковое число элементов и все соответствующие упорядоченные значения равны между собой, то два множества считаются равными. Скорость работы этой операции можно оценить как O(n), где n – число элементов в множествах. К примеру, если бы данные нельзя было упорядочить, как это происходит в динамических массивах, то объем вычислений при сравнении составил бы O(n^2). А это уже существенно больше, чем O(n). По аналогии можно получить быстрые алгоритмы при определении вхождения одного множества в другое, то есть, операции меньше и больше. Я напомню, что одно множество setB входит в другое setA, если множество setA содержит все те же самые элементы, что и множество setB:
Например, возьмем множества setA = {7, 6, 5, 4, 3} setB = {3, 4, 5} тогда операция setB < setAвернет True, а операция setB > setAзначение False. Если же в множестве setB имеется значение, не входящее в множество setA, то обе операции сравнения на больше и меньше вернут False. Например: setA = {7, 6, 5, 4, 3} setB = {3, 4, 5, 11} то False:
setB < setA
Наконец, если оба множества равны между собой, то операции сравнения на больше и меньше также вернут False: setA = {7, 6, 5, 4, 3} setB = {7, 6, 5, 4, 3} получим: False: setB < setA
Давайте теперь посмотрим, как реализуется алгоритм сравнения множеств на меньше или больше. Мы уже знаем, что легко получить упорядоченные значения двух множеств. Например, если даны множества: setA = {5, 7, 6, 2, 4, 3} setB = {3, 6, 4} то после упорядочения по возрастанию получим последовательности: setA: 2, 3, 4, 5, 7, 6
Затем, при сравнении setB < setA, первым делом проверяем, чтобы число элементов в множестве setB было меньше, чем в setA. Если это не так, то множество setB заведомо не может входить в множество setA. После этого сравниваем граничные значения множеств: наименьшее и наибольшее значения множества setB не должны выходить за диапазон граничных значений множества setA. Если все выполняется, то далее, последовательно проходим по элементам большего множества setA и сравниваем с первым значением множества setB. Как только значения элементов совпали, сравниваем последующие величины множества setA со вторым значением множества setB. Если при полном проходе по setA находим все совпадения со значениями множества setB, то делаем вывод, что множество setB входит в множество setA и операция сравнения setB < setA возвращает True. Если не было найдено хотя бы одно значение в множестве setB, то возвращается False. Причем проверку можно прерывать, если текущее проверяемое значение в setB оказывается меньше текущего значения из setA. Вычислительная сложность этой операции с точки зрения О большого составляет O(n), где n – число элементов в большем множестве. Как видите, использование бинарного дерева в качестве основы для хранения данных в множествах позволяет создавать алгоритмы сравнения множеств с линейной сложностью O(n). Операции над множествамиВо второй части занятия рассмотрим принципы работы алгоритмов пересечения, объединения, вычитания и симметричной разности двух множеств. Я напомню, что:
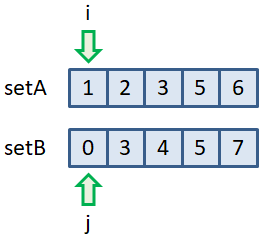
Давайте посмотрим, как можно реализовать эти алгоритмы, используя упорядоченные последовательности значений. Начнем с пересечения двух множеств. Алгоритм пересечения двух множествПусть имеются множества: setA = {3, 5, 2, 1, 6} setB = {7, 0, 3, 4, 5} После упорядочения их значений, получаем последовательности:
Элементы списка множества setA будем перебирать с помощью индекса i, а элементы множества setB – с помощью индекса j. Наша задача выделить общие значения обоих множеств. Поэтому вначале проверяем на равенство элементы с индексами i и j. Если они не равны, то увеличиваем на единицу индекс, который соответствует меньшему значению элемента. В данном примере – это индекс j, т.к. он ведет на элемент со значением 0. Далее, сравниваем значения 1 и 3. Так как 1 < 3, то увеличиваем индекс i на единицу. Получаем следующую пару 2 и 3 и, так как 2 < 3, то снова увеличиваем i на единицу. Теперь оба значения в последовательностях равны 3 – совпадают. Поэтому заносим это значение в результирующее множество setA & setB. Далее можно увеличивать любой индекс (или оба вместе, т.к. в множествах значения не повторяются). Пусть так и будет. Получаем пару 5 и 4. Так как 5 > 4, то увеличиваем индекс j на единицу. Получаем равные значения 5, поэтому добавляем его в результирующее множество. Увеличиваем оба индекса на единицу, получаем значения 6 и 7. В результате, множество setA & setB будет содержать два элемента со значениями 3 и 5: setA & setB = {3, 5} которые являются общими для обоих исходных множеств. В итоге получаем линейный объем вычислений для этой и всех последующих операций над множествами. Алгоритм объединения двух множествПо аналогии работает алгоритм объединения двух множеств. Только теперь в результирующее множество добавляются все элементы из обоих множеств, но ровно один раз, чтобы не было дублирования. Пусть даны те же самые множества с такими же упорядоченными значениями:
Вначале сравниваем пары элементов по индексам i и j на равенство. Если они не равны (как в нашем примере), то в результирующее множество добавляется наименьшее значение. Затем, увеличиваем индекс j на единицу, т.к. он соответствует элементу с меньшим значением 0. Получаем пары 1 и 3. Добавляем в третье множество наименьшее значение 1 и увеличиваем индекс i на единицу. Имеем пары 2 и 3. То же самое, добавляем 2 в третье множество и снова увеличиваем i на единицу. Теперь у нас два одинаковых значения 3 и 3. Добавляем 3 в результирующее (третье) множество и увеличиваем оба индекса на единицу. Повторяем эту операцию пока не достигнем конца обоих множеств. В итоге, у нас получится следующий результат их объединения: setA | setB = {0, 1, 2, 3, 4, 5, 6, 7} Алгоритм вычитания двух множествСнова воспользуемся теми же самыми множествами с набором упорядоченных значений:
Тогда для реализации алгоритма вычитания: setA - setB достаточно сформировать третье множество setC, в котором будут находиться значения из множества setA, не принадлежащие множеству setB. Вначале мы имеем пары значений 1 и 0 в множествах setA и setB (в соответствии с индексами i, j упорядоченных коллекций). Так как значения разные и 0 меньше 1, то увеличиваем индекс j на единицу. Получаем следующую пару 1 и 3. Здесь 1 меньше 3, значит, значения 1 точно нет в множестве setB и мы 1 добавляем в результирующее множество setC. Увеличиваем индекс i на единицу. Здесь 2 меньше 3, поэтому 2 также помещаем в множество setC и увеличиваем индекс i на единицу. Получаем равные значения 3 и 3, поэтому смещаем оба индекса i, j на следующий элемент. Следующая пара 5 и 4. Так как 5 больше 4, то увеличиваем индекс j на единицу. Имеем пары 5 и 5, поэтому оба индекса увеличиваем на один. Последняя пара имеет разные значения 6 и 7, поэтому значение 6 из множества setA добавляем в результирующее множество setC. В итоге получаем результат вычитания: setC = {1, 2, 6} Алгоритм симметричной разности двух множествФактически, симметричная разность двух множеств – это их объединение с отбрасыванием общих значений. Поэтому алгоритм очень похож на алгоритм объединения множеств. Также предположим, что у нас два множества со следующими наборами упорядоченных значений:
Вначале сравниваем пары элементов по индексам i и j на равенство. Если они не равны (как в нашем примере), то в результирующее множество добавляется наименьшее значение. Затем, увеличиваем индекс j на единицу, т.к. он соответствует элементу с меньшим значением 0. Получаем пары 1 и 3. Добавляем в третье множество наименьшее значение 1 и увеличиваем индекс i на единицу. Имеем пары 2 и 3. То же самое, добавляем 2 в третье множество и снова увеличиваем i на единицу. Теперь у нас два одинаковых значения 3 и 3, поэтому пропускаем это значение и увеличиваем оба индекса на единицу. Повторяем эту операцию пока не достигнем конца обоих множеств. В итоге, у нас получится следующий результат их симметричной разности: setA ^ setB = {0, 1, 2, 4, 6, 7} Вот так, достаточно быстро можно реализовывать операции с множествами, используя бинарные деревья для их представления. Курс по структурам данных: https://stepik.org/a/134212 Видео по теме |