|
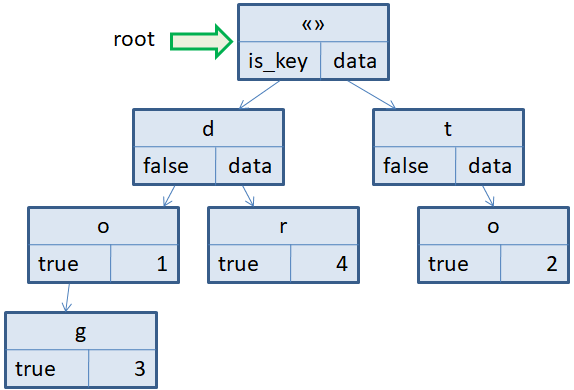
Префиксное (нагруженное, Trie) дерево. Ассоциативные массивыКурс по структурам данных: https://stepik.org/a/134212 Мы продолжаем курс по структурам данных. На этом занятии речь пойдет о префиксных (нагруженных или Trie) деревьях. Названий несколько, но на мой взгляд лучше подходит префиксное дерево. Его я и буду использовать. Так вот, есть одна достаточно распространенная структура данных, которая использует такие деревья в своей работе – ассоциативные массивы, когда доступ к данным осуществляется по ключам (как правило, строкам), а не по индексам (порядковым номерам). В качестве ключей может быть использована любая байтовая последовательность символов. Первый вопрос, как представляются эти данные в памяти компьютера, и как выполняются основные операции записи и считывания данных. Давайте предположим, что у нас имеется следующий ассоциативный массив с наборами ключ-значение: ar["do"] = 1; ar["to"] = 2; ar["dog"] = 3; ar["dr"] = 4; Для создания связей между ключами "do", "to", "dog", "dr" и соответствующими значениями формируется префиксное дерево, которое в данном случае будет иметь вид:
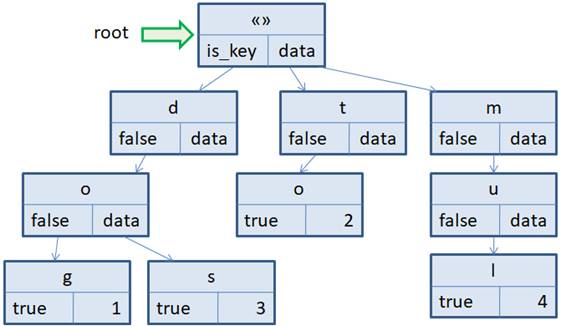
Здесь в каждом узле хранится ровно один символ ключа (кроме корневого узла, который не хранит никакого символа и является попросту отправной точкой). У корня два потомка, так как ключи в нашем примере могут начинаться или с символа d или с символа t. Далее, узел d также имеет два потомка, так как после символа d может идти или символ o или символ r. А узел t имеет только одного потомка, т.к. у нас определен только один ключ «to», то есть, после t может идти только символ o. По тому же принципу узел o имеет одного потомка с символом g. То есть, проходя по соответствующим узлам дерева, мы будем получать различные ключи. Как вы уже заметили, каждый узел префиксного дерева содержит два поля: is_key и data. Зачем они нужны? Поле is_key, которое принимает булевы значения true и false, отмечает, является ли данная вершина дерева ключом ассоциативного массива или же просто промежуточной вершиной. Например, символы d и t отмечены как false. Значит, они не образуют самостоятельных ключей. Именно поэтому, если в программе будет идти обращение к ключу: int val = ar["d"]; то мы получим некоторое предопределенное значение для несуществующего ключа. (Для контейнера map – это значение 0). То есть, ключ в дереве не будет найден. А вот если написать: int val = ar["do"]; то переменная val будет равна 1, потому что узел с символом o имеет значение true поля is_key. То есть, это поле is_key говорит нам, является ли найденный фрагмент последовательности данных ключом или нет. В частности, если бы в нашей программе не был определен ключ: ar["do"] = 1; то тогда узел с символом o имел бы флаг is_key равный false и при обращении к массиву по ключу «do» мы бы знали, что данный ключ в префиксном дереве отсутствует. А вот ключ «dog» присутствует. Поэтому символ o становится просто промежуточным для ключа «dog». Вот для этого и нужно поле is_key. Второе поле data просто содержит данные, связанные с тем или иным ключом. Причем, данные можно сохранять только в тех вершинах, у которых is_key равен true. Вот общий принцип представления данных ассоциативных массивов с помощью префиксных (или, как еще говорят, нагруженных) деревьев. Алгоритм формирования префиксного дереваДавайте детальнее ознакомимся с алгоритмом формирования префиксного дерева. Предположим, создаются четыре пары ключ-значение: ar["dog"] = 1; ar["to"] = 2; ar["dos"] = 3; ar["mul"] = 4; Изначально, префиксное дерево имеет только корневую вершину без каких-либо символов. Первый ключ, который в него добавляется – это строка «dog». Очевидно, нам последовательно нужно сформировать три вершины, которые следуют друг за другом. Причем вершины d и o имеют флаг is_key = false, а последняя вершина g – значение is_key = true, т.к. она хранит непосредственно данные для ключа «dog». По аналогии добавляются вершины для ключа «to». Также два отдельных узла от корневого с данными в вершине o. Следующий ключ «dos». Вершины d и o уже имеются в префиксном дереве, поэтому достаточно добавить еще одну вершину s, как дочернюю от вершины o. Вершину s помечаем is_key=true и сохраняем данные data=3. Последний ключ «mul» образуется тремя новыми узлами дерева, начиная от корневой вершины. В узле l прописываем is_key=true и data=4. Как видите, формирование префиксного дерева выполняется достаточно просто. Объем вычислений для добавления нового ключа с точки зрения O большого, равно O(|key|), где |key| - длина (число символов) ключа.
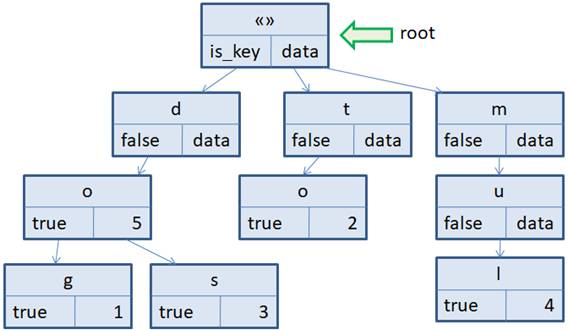
Алгоритм поиска ключа в префиксном деревеПредположим, у нас имеется ранее сформированное префиксное дерево. И мы хотим взять из массива значение по некоторому ключу, например, «dos»: val = ar["dos"] В этом случае выбирается первый символ ключа – это «d» и в дереве среди потомков корневой вершины ищется вершина с этим символом. Она у нас есть, поэтому указатель p переходит к этой вершине (ссылается на эту вершину). Следующий символ в ключе – это «o». Поэтому среди потомков вершины d ищется вершина с символом «o». Она также присутствует в дереве и указатель p переходит к ней. Наконец, последний символ ключа – это «s». Среди дочерних вершин узла o ищется вершина с символом «s». И указатель перемещается на нее. Далее проверяется, если эта вершина является ключевой, а не промежуточной, то есть флаг is_key=true, значит, ключ «dos» в нашем префиксном дереве присутствует и мы возвращаем данные, которые хранятся в поле data, то есть, значение 3. Теперь предположим, что мы хотим обратиться в ассоциативном массиве по ключу «do»: val = ar["do"] Также начинаем движение от корня дерева. Переходим сначала к узлу «d», затем, к узлу «o». Этот узел присутствует в дереве, но значение поля is_key=false, то есть, узел «o» промежуточный, а не конечный для какого-либо ключа. Это значит, что ключа «do» в нашем префиксном дереве нет. И тогда, можно вернуть некоторое значение по умолчанию, которое соответствует отсутствующему ключу. Другой случай, когда нам нужно найти ключ, например, «till»: val = ar["till"] Также начинаем с корня и переходим к узлу t. Далее, у этого узла ищем потомка с символом «i». Но его нет. Следовательно, ключ «till» в нашем префиксном дереве отсутствует. Я думаю, что из этих примеров вам понятен принцип работы алгоритма поиска ключей в префиксном дереве. Если мы проходим по всем символам ключа и находим в конце узел с меткой is_key=true, значит, ключ присутствует в дереве. Во всех остальных случаях – отсутствует. Временная сложность алгоритма поиска ключа равна O(|key|). Алгоритм удаления ключа из префиксного дереваДавайте теперь представим, что нам нужно удалить какой-либо ключ из ассоциативного массива (префиксного дерева). Пусть имеется следующее нагруженное дерево:
Здесь представлены следующие ключи: «do», «dog», «dos», «to», «mul». Сначала мы выполним удаление ключа «do». Из структуры дерева видно, что узел o является промежуточным для узлов g и s. Поэтому его и нужно пометить промежуточным для алгоритма поиска ключей, то есть флаг is_key приравнять false. Все, теперь в дереве нет ключа «do». Другой пример удаления ключа «mul». За него отвечают три последовательных узла m, u, l. Узел l – листовой (у него нет потомков). Поэтому здесь есть два варианта удаления. Первый, это также пометить узел l не ключевым, то есть is_key=false. Во втором варианте, исключить из дерева все листовые вершины, связанные с ключом «mul». Удаление происходит с последнего узла l. После этого узел u становится листовым, значит, его также можно удалить. Наконец, узел m, тоже листовой, удаляется из префиксного дерева. В результате мы удалили все три узла, связанных только с этим одним ключом «mul». А вот если бы мы по этому же алгоритму стали бы удалять ключ «dos», то после удаления листовой вершины s, вершина o остается промежуточной, содержащей потомка g. Поэтому дальнейшее удаление по цепочки останавливается. Какой же алгоритм удаления ключей использовать? Обычно, это вытекает из конкретной практической задачи. Если ожидается построение больших нагруженных деревьев, то считается достаточным изменение флага is_key на значение false. К большой потери памяти это не приведет, но несколько ускорит работу алгоритма удаления. Если же дерево небольшое, то целесообразно физически удалять ненужные вершины. Вообще, с помощью последовательного удаления листовых вершин, которые не связаны ни с одним ключом, можно выполнять сжатие префиксного дерева. Это можно использовать, как отдельный алгоритм для оптимизации нагруженного дерева. И вызывать его не каждый раз при удалении ключа, а после удаления определенного количества ключей ассоциативного массива. Временная сложность алгоритма удаления ключа равна O(|key|). ЗаключениеВообще нагруженные деревья часто эффективнее по памяти, чем хэш-таблицы. Это связано с тем, что у множества ключей в нагруженном дереве совпадают префиксы. Например, для ключей «dog», «dos» единый префикс «do», то есть, используется одна и та же пара вершин d и o для этих двух строк. Если в последующем будут добавлены новые ключи с тем же префиксом, например «dota», «doka» и т.п., то будут использованы уже существующие вершины и добавлены новые. Отсюда же хорошо видно, почему такие деревья получили название префиксное. Мы можем для любой начальной последовательности символов (префиксу) получить наборы ключей (слов), которые ему соответствуют. Например, в нашем примере дерева по префиксу «do» можно выделить два ключа: «dog» и «dos». Или, по префиксу «d» - три ключа: «do», «dog» и «dos». И эта процедура выполняется достаточно быстро – быстрее, чем при других способах организации данных. Именно поэтому префиксные деревья были положены в основу первых алгоритмов подсказки слов в мессенджерах или в ОС системах на базе Unix в командной строке. Поэтому область применения такой структуры данных не ограничивается только ассоциативными массивами. Курс по структурам данных: https://stepik.org/a/134212 Видео по теме |