|
Односвязный список. Структура и основные операцииКурс по структурам данных: https://stepik.org/a/134212 Мы продолжаем курс по структурам данных. На прошлых занятиях мы подробно ознакомились со статическими и динамическими массивами. Пришло время сделать следующий шаг и рассмотреть новую структуру – односвязный список. Я начну с основных недостатков динамических массивов. Как мы уже говорили, если физического размера недостаточно, то создается новый массив длиной, скажем, в два раза больше прежнего и в первую половину копируются данные из первого массива. Это достаточно ресурсоемкая операция, составляющая O(n), особенно, когда число элементов n стремительно растет. Кроме того, все данные должны храниться в непрерывной области памяти, а это дополнительная проблема для массивов очень больших размеров: не так просто бывает найти достаточный и непрерывный объем памяти. Давайте попробуем решить эти проблемы. Что если при увеличении физического размера динамического массива мы просто выделим еще один такой же кусок где то в памяти, то есть, данные уже не будут идти строго друг за другом, а находиться в разных областях. Очевидно, при таком подходе нам не пришлось бы копировать уже имеющиеся данные в новый массив, и не требовалось бы искать все большую и большую непрерывную область памяти. Мало того, скорость добавления нового элемента происходила бы за константное время O(1) – значительно быстрее, чем в классическом динамическом массиве. Видите, сколько сразу плюсов мы получаем от такой идеи организации данных! Осталось только выяснить, как нам осуществить переход от последнего элемента первого массива к первому элементу второго массива? Самое простое и очевидное что можно сделать – это хранить в последнем элементе ссылку на следующий блок данных. А тот, второй блок, должен хранить ссылку на следующий и так далее. Получаем связанную структуру из отдельных блоков памяти. Словно паровозик: во главе стоит первый блок, затем цепляется второй, потом третий и так до конца.
А теперь возведем такую структуру в некий абсолют: вообще откажемся от массивов, а вместо них определим отдельные элементы, которые будут ссылаться друг на друга, пока последний элемент не будет иметь ссылку на NULL, или None, или какое-либо другое предопределенное значение, которое означает конец последовательности.
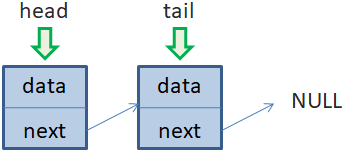
Такая структура данных, в которой элементы ссылаются друг на друга по порядку в одном направлении, начиная от первого и до последнего, получила название односвязный список. Добавление элементов в конец и начало односвязного спискаДавайте теперь посмотрим, какие основные операции можно выполнять с этой структурой данных. Начнем с операций добавления новых элементов в конец и начало списка. Предположим, что в списке всего два объекта. На первый элемент (объект) всегда ссылается переменная head, а на последний – переменная tail:
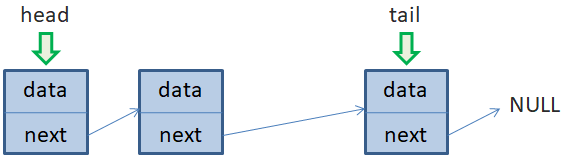
Мы хотим добавить в конец еще один элемент. Для этого, сначала нужно создать сам объект нового элемента списка (пусть на него ссылается временная переменная node). Затем, по ссылке tail выбираем последний элемент списка (который скоро станет предпоследним) и ссылку next меняем со значения NULL на значение адреса добавляемого объекта node. В свою очередь, у объекта node ссылку next устанавливаем равную NULL. И последнее, переменной tail присваиваем значение node так, чтобы tail указывала на последний элемент списка.
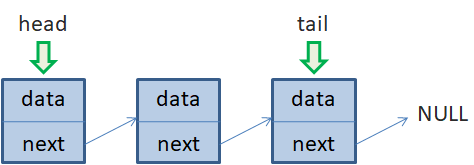
Как видите, все достаточно просто. Скорость выполнения этой операции с точки зрения О большого составляет O(1). Часто в языках программирования эту операцию реализуют методом с названием push_back(). Давайте теперь посмотрим, как выполняется добавление элемента в начало односвязного списка. Пусть у нас имеются три элемента. На первый, по-прежнему, ссылается переменная head, а на последний – переменная tail:
Вначале также создаем новый объект, на который ссылается временная переменная node. Затем, значение ссылки next добавляемого элемента приравниваем значению head – адресу первого элемента списка, после чего head становится вторым. Поэтому присваиваем его значению переменной node так, чтобы head ссылалась на первый элемент списка:
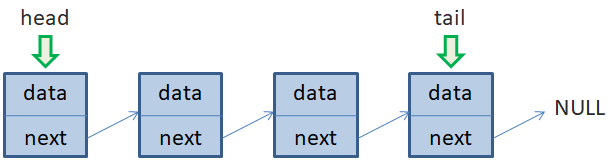
Скорость выполнения этой операции также O(1), то есть, происходит за константное время и не зависит от размера списка (числа его элементов). Часто в языках программирования эту операцию реализуют методом под названием push_front(). Доступ к произвольному элементу односвязного спискаДавайте теперь посмотрим, как можно обратиться к произвольному элементу односвязного списка. Предположим, у нас имеется список из четырех объектов:
Очевидно, для получения доступа к данным первого или последнего элемента достаточно воспользоваться ссылками head и tail. Например: head.data – доступ к
данным первого элемента
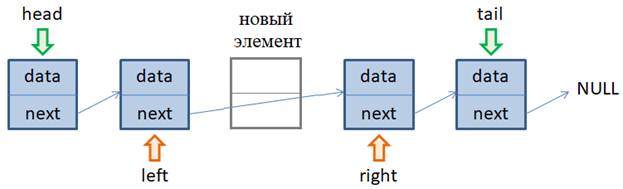
Но как нам обратиться ко 2-му или 3-му элементу этого списка? Для этого придется по цепочке двигаться от первого элемента до заданного k-го элемента, используя ссылки next. Обычно для этого создают временную переменную (ссылку на объект), допустим, с именем node. Изначально node равен head, то есть, ссылается на первый элемент. Чтобы перейти к следующему элементу нужно node присвоить адрес следующего объекта. А этот адрес хранится в переменной next текущего объекта. То есть, нам нужно выполнить команду: node = node.next И указатель node будет ссылаться на второй элемент односвязного списка. Далее, можем действовать по циклу, перебирая все элементы от начала и до конца, пока значение next не будет равно NULL (или любому другому терминальному значению). Это значит, для доступа к произвольному k-му элементу, мы должны последовательно перебрать все предыдущие элементы. В итоге, сложность этой операции с точки зрения О большого, составляет O(n), где n – общее число элементов в односвязном списке. Как видите, в отличие от массивов, где доступ к произвольным элементам составляет O(1), здесь все несколько сложнее. Это та цена, которую мы платим за возможность быстрого добавления элементов в односвязный список, а также возможность хранить данные в разных областях памяти компьютера. Вставка элемента в односвязный списокПостепенно мы с вами дошли до вставок новых элементов в связный список. Как это делается и насколько вычислительно сложно? Чтобы все было предельно просто и понятно, я возьму небольшой односвязный список из четырех элементов. Наша задача вставить пятый новый элемент после второго.
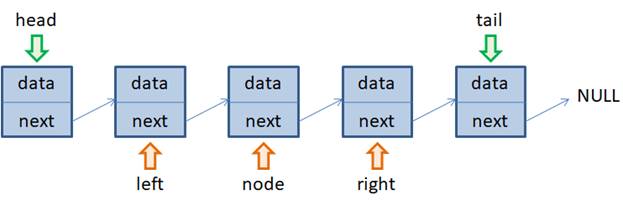
Очевидно, нам здесь понадобятся ссылки left и right на предыдущий и следующий элементы относительно добавляемого. Как их получить вы уже знаете: мы перебираем все элементы с самого начала и фиксируем два соседних, между которыми вставляется новый объект. Далее, создаем новый элемент в памяти компьютера, на который ссылается временная переменная node. Осталось только настроить связи ссылок next у объектов left и node. Из рисунка хорошо видно, что ссылка next объекта left должна вести на node, поэтому делаем присваивание: left.next = node А ссылка next объекта node должна вести на объект right, имеем: node.next = right Все, новый объект вставлен в односвязный список. Часто в языках программирования эта операция реализуется командой insert(). Самое сложное в вычислительном плане здесь – это получить ссылку left объекта, после которого планируется вставлять новый элемент. В общем случае для этого требуется O(n) операций, что не мало (n – число элементов в списке). Однако если эта ссылка у нас уже есть, то сама операция вставки занимает время O(1). А это уже значительно быстрее, чем у массивов. Поэтому сложность зависит от конкретного использования односвязного списка. Если у нас в распоряжении будут уже готовые ссылки на объекты, после которых предполагаются вставки, то скорость выполнения операций будет высока. В общем же случае, когда нужно сначала найти объект, а потом вставить новый, то сложность становится линейной O(n). Удаление элементов из односвязного спискаВ заключение этого занятия рассмотрим обратные операции по удалению элементов из односвязного списка. Начнем с удаления промежуточных объектов. Давайте предположим, что в списке пять элементов и нам нужно удалить объект node:
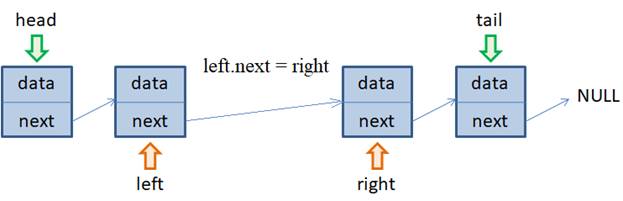
Для этого достаточно у предыдущего объекта left переопределить ссылку next на объект right: left.next = right и освободить память, занимаемую объектом node:
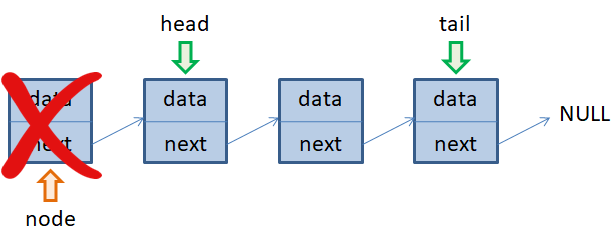
Скорость самой операции удаления элемента node из односвязного списка выполняется за константное время O(1). Но для получения ссылок left и right требуется O(n) операций. Поэтому, в общем случае, имеем объем вычислений, равный O(n), где n – число элементов в списке. В языках программирования эта операция часто реализуется командой erase(). Последнее, что мы рассмотрим на этом занятии – это удаление первого и последнего элементов односвязного списка. Первый элемент удаляется относительно просто. Нам достаточно переместить указатель head на следующий элемент и освободить память, занимаемую элементом node:
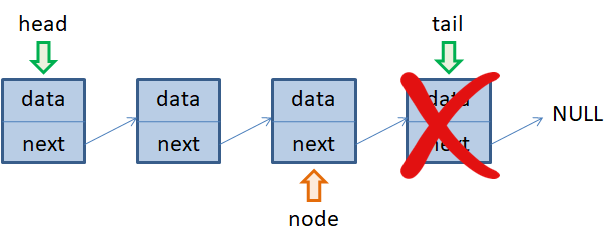
Как видите, все предельно просто. Скорость этой операции с точки зрения О большого O(1) и часто реализуется командой pop_front(). При удалении последнего элемента в односвязном списке нам необходимо сначала получить ссылку на предпоследний элемент, затем, освободить память последнего элемента tail. Изменить значение tail на node: tail = node и поменять значение ссылки next объекта node на NULL: node.next = NULL
Скорость удаления самого элемента составляет O(1), но переход к предпоследнему элементу O(n). Поэтому общая вычислительная сложность этого алгоритма составляет O(n). В языках программирования эта операция часто реализуется командой pop_back(). ЗаключениеПодведем общие итоги этого занятия. Самые быстрые операции – это добавление элементов в начало и конец списка и удаление с начала списка. Остальные операции имеют сложность O(n).
На следующем занятии мы продолжим эту тему и посмотрим на пример реализации односвязного списка на языке программирования. Курс по структурам данных: https://stepik.org/a/134212 Видео по теме |