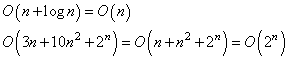О большое, массивы
О большое (Big O) - верхняя оценка сложности алгоритмов
О большое (Big O). Случаи логарифмической и факториальной сложности
Статический массив. Структура, его преимущества и недостатки
Примеры реализации статических массивов на C++
Динамический массив. Принцип работы
Реализация динамического массива на Python
Реализация динамического массива на С++ с помощью std::vector
Обучающие курсы
Python Python ООП Структуры данных Django C/C++
Телеграм-каналы
Канал selfedu_rus Python Django Машинное обучение Java и С++
Наш канал

О большое (Big O). Случаи логарифмической и факториальной сложности

Курс по структурам данных: https://stepik.org/a/134212

Мы продолжаем тему «О большое» по оценке вычислительной сложности различных алгоритмов.

Неважная сложность

На предыдущем занятии мы увидели, что сложность алгоритма с двумя вложенными циклами:

for x in range(n):
    for y in range(n):
        print(x, y)

с позиции Big O оценивается как:

Давайте теперь после вложенного цикла добавим еще один цикл:

for x in range(n):
    for y in range(n):
        print(x, y)
 
for t in range(n):
    print(t)

Формально, Big O для этого случая можно записать в виде:

Нужно ли здесь что то упрощать или оставить в таком виде? Смотрите, слагаемое n значительно меньше при . И с точки зрения Big O оно становится не значимым, а значит, может быть отброшено. Поэтому результат запишется так:

Естественно, здесь возникает вопрос, какие слагаемые считать значимыми, а какие не значимыми в О большом? Полагают, если одно слагаемое может принимать значения более чем в два раза больше другого, значит, оно значимое. Соответственно, второе – незначимое. Очевидно, если , то , поэтому n можно уже не учитывать при определении сложности алгоритма. Динамика роста настолько перекрывает динамику роста n, что n становится уже незначимым слагаемым.

Вот еще примеры, в которых также отбрасываются незначащие слагаемые:

и так далее. Все незначимые слагаемые, с точки зрения скорости роста вычислительной сложности алгоритма, отбрасываются. Но, если какое-либо слагаемое не определено в Big O, например:

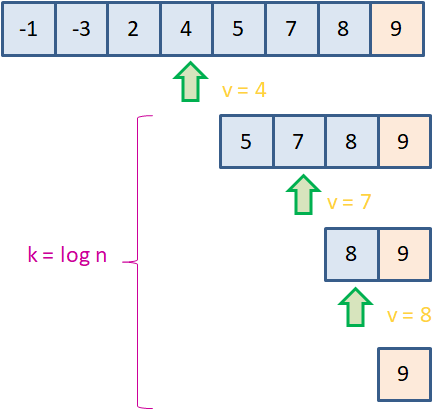
и мы ничего не знаем про A, то эта запись остается в неизменном виде.

Алгоритмы с логарифмической сложностью

Довольно часто на практике можно столкнуться с алгоритмами, имеющими логарифмическую сложность выполнения. Яркий представитель – бинарный поиск. Кратко опишу его. Если у нас имеется отсортированный список чисел, то найти какое-либо значение можно методом половинного деления:

Допустим в последовательности необходимо найти элемент со значением 9. Тогда на первом шаге выбирается центральный элемент со значением 4. Далее, мы видим, что 9 больше 4, значит, для дальнейшего поиска нужно взять вторую половину этого списка. И так далее, пока не будет найдено искомое значение. На Python этот алгоритм можно реализовать так:

d = [-1, -3, 2, 4, 5, 7, 8, 9]
n = len(d)
 
search_v = 9
left, right = 0, n-1
 
while left <= right:
    middle = (left + right) // 2
    v = d[middle]
    if v == search_v:
        print(v, middle)
        break
    elif v < search_v:
        left = middle + 1
    elif v > search_v:
        right = middle - 1
else:
    print("значение не найдено")

Можно заметить, что в наихудшем случае число делений пополам составит величину:

Например, при n = 8 максимальное число делений равно трем. Эта величина и будет определять вычислительную сложность алгоритма в терминах Big O:

Обратите внимание, что основание логарифма – это константа, которую, обычно, не указывают. Подразумевается, что оно больше единицы.

То есть там, где происходит иерархическое разбиение данных и последующая обработка оставшейся части, как правило, получается логарифмическая сложность алгоритма.

Алгоритмы с факториальной сложностью

Следующий распространенный класс алгоритмов – это, так называемые, NP-полные задачи, в которых приходится делать полный перебор всех вариантов, чтобы найти искомое решение. Например, мы хотим написать алгоритм по сборку пазла. В самом простом случае, можно перебрать все возможные варианты из фрагментов и выбрать нужный. Если число фрагментов обозначить через n, то вариаций их перебора составит величину:

Действительно, если фрагментов всего n = 2, то будем иметь:

варианта перебора (меняем между собой и все). Если n = 3, то:

вариантов перебора. Это легко проверить, их действительно всего шесть. И так далее. В нотации О большого имеем вычислительную сложность такого алгоритма, равную:

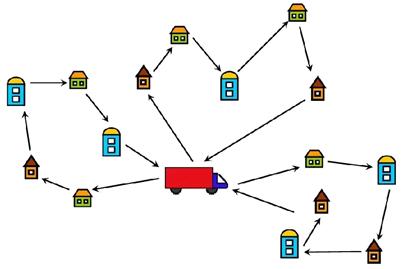
Другой похожий алгоритм, который часто приводят в качестве примера NP-полной задачи – это решение задачи коммивояжера. В ней необходимо выстроить наикратчайший маршрут из некоторой начальной точки, проходящий через все города:

Если число городов принять за n, то необходимо перебрать n! вариантов, чтобы найти лучшее решение. Причем, на сегодняшний день эта задача не имеет быстрого алгоритма, т.е. чтобы найти наилучшее решение нужно сделать полный перебор всех возможных вариантов.

Как вы уже догадались, вычислительная сложность данного алгоритма составляет:

И подобных алгоритмов с объемом вычислений n! довольно много. Неприятность здесь в том, что функция:

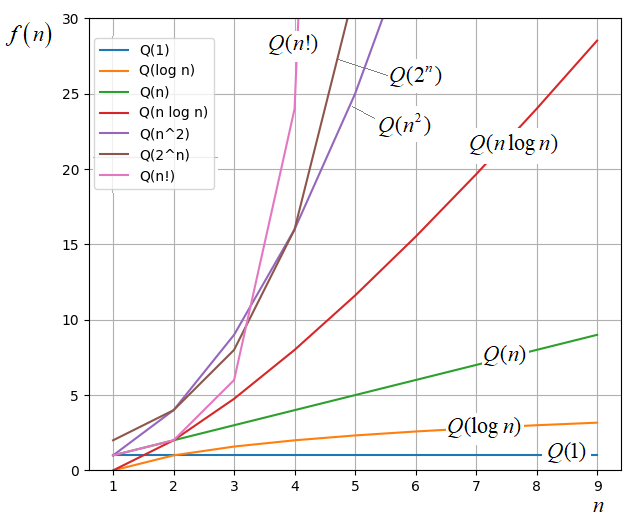
растет очень быстро. А зачит, это одни из самых сложных алгоритмов (в вычислительном плане). Как только мы получаем такую оценку сложности, есть смысл подумать о более простых подходах, дающие пусть и не точное, но близкую к точному решение. Конечно, если n в задачах можеть быть от 10 и более.

Порядок возрастания вычислительной сложности алгоритмов

Чтобы вы лучше представляли уровень сложности, связанный с различными выражениями для Big O, я приведу графики зависимостей для тех формул, что мы с вами получили:

Ожидаемо, наименьшее значение показывает , затем , далее , после него идет и, наконец, . Проектировать алгоритмы следует так, чтобы рост функции для О большого был как можно медленнее. Разумеется, не всегда удается получать относительно быстрые алгоритмы, но имея оценку О большого для разных реализаций, нужно выбирать тот, которому соответствует более пологая зависимость .

Как правило, программист редко вычисляет оценку Big O для своего алгоритма. Лучше, если это делает специально обученный сотрудник, знакомый с математикой, лежащей в основе метрики О большого. Иначе, легко ошибиться и сделать неверные выводы. Но знать общие принципы и правильно понимать выражения для Big O должен каждый уважающий себя программист. Довольно часто приходится видеть эту нотацию, как характеристику сложности того или иного алгоритма. И без ее знания легко совершить ошибку, а значит, выстроить не лучший программный код.