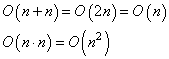|
О большое (Big O) - верхняя оценка сложности алгоритмовКурс по структурам данных: https://stepik.org/a/134212 Мы начинаем курс по структурам данных. Чтобы вы сразу представляли о чем пойдет речь приведу примеры таких структур:
Зачем они вообще нужны? Дело в том, что не существует единого, универсального подхода представления и хранения данных в программе и для каждой конкретной задачи следует выбирать свой эффективный способ организации данных в памяти компьютера. Чтобы уметь это делать, как раз и нужно знать основные, наиболее распространенные структуры данных. Но прежде чем мы
перейдем непосредственно к рассмотрению этих структур, нам нужно разобраться,
как оценивать и сравнивать между собой скорости работы алгоритмов. Опять же
единого ответа на этот вопрос нет. На заре вычислительной техники предлагалось сравнивать
число элементарных арифметических операций (сложения, умножения, деления),
которые совершает алгоритм в процессе своей работы. Однако так можно делать или
для очень простых программ или для математических алгоритмов. Еще можно
попробовать замерить скорость работы алгоритма в миллисекундах. Однако на
разном железе с разной производительностью мы будем получать разные результаты
для одной и той же программы. И, кроме того, время работы может нелинейно
возрастать с увеличением размерности (объема) входных данных. Например, все
медленные алгоритмы сортировки элементов массива имеют квадратическую сложность
верхнюю границу динамики изменения вычислительной сложности алгоритма в зависимости от размера входных данных. Чаще всего именно
она интересна разработчикам. Например, для тех же медленных алгоритмов
сортировки элементов массива длиной n, верхняя граница их
вычислительной сложности (т.е. наихудший случай) определяется как В рамках данного курса я не буду углубляться в фундаментальное математическое определение О большого. Программист чаще всего следует некоторым разумным правилам при оценке сложности алгоритма. И те правила, о которых мы дальше будем говорить, базируются на строгих математических законах. Сложность выполнения константных операцийДавайте представим, что мы на языке Python выполняем команды, которые не зависят от размера входных данных. Например: var_a = 10 inf = float('inf') print(inf) Каждая строчка выполнится за определенное время. Предположим, мы измерили это время, и оно оказалось равным 1 мс. Вопрос. Какова вычислительная сложность каждой команды? Мы с вами прекрасно понимаем, что полученное время t = 1 мс будет разным на разных компьютерах. Поэтому такая характеристика не совсем корректна. По большому счету мы можем здесь сказать только одно: в каждой строчке выполняется одна операция за одно и то же константное время. В нотации О большого это записывается так: O(1) Здесь 1 означает выполнение одной операции. А конкретное время выполнения этой операции, как бы вынесено за скобки и отбрасывается. При качественном сравнении скорости работы алгоритмов подобные константы не имеют большого значения. То есть, с точки зрения О большого любая константа может быть отброшена. Например: O(10) = O(1)
Здесь C – константа. А раз это так, то последовательное выполнение трех константных по времени операций даст с точки зрения О большого, следующее выражение: O(1 + 1 + 1) = O(3) = O(1) То есть, О(1) лишь показывает, что в алгоритме выполняется одна операция за некоторое константное время и при этом не важно, сколько команд входит в эту операцию: одна, две, три. Главное, чтобы все они выполнялись за фиксированный промежуток времени и не зависели от размера входных данных. Вот так следует воспринимать O(1). Линейная сложность выполнения алгоритма Давайте теперь усложним алгоритм и представим, что имеется массив (список) из n элементов. Для простоты это будут произвольные числа: lst = [1, 4, 10, -5, 0, 2, 3, ..., 18, 32] # n элементов Затем, мы их последовательно в цикле перебираем и выводим на экран: for x in lst: print(x) Какова сложность этого алгоритма? Очевидно, что число итераций цикла зависит от размерности массива n. Чем больше n, тем больше итераций нужно сделать в цикле. То есть, цикл зависит от размера входных данных. Так вот, нотация О большое должна показывать динамику этой зависимости, то есть, изменение сложности алгоритма от размера n входных данных. И в данном случае эта величина равна: O(n) Обратите внимание, здесь n – уже переменная, а не константа. Так как в общем случае при работе с массивами и другими упорядоченными коллекциями мы полагаем, что n может бесконечно увеличиваться. Здесь всегда следует помнить, что О большое показывает верхнюю границу, то есть соответствует худшему случаю работы алгоритма (в вычислительном плане). Из записи O(n) хорошо виден линейный характер зависимости сложности работы цикла от размера массива n. Но здесь можно задать резонный вопрос. А что если в цикле будет выполняться сразу несколько команд, например, так: for x in lst: x += 1 print(x) Возрастет ли тогда сложность с точки зрения О большого? Будет ли она равна: O(2n) В действительности нет. Всегда следует помнить, что О большое показывает лишь динамику изменения вычислительной сложности алгоритма, ее зависимость от размера входных данных и не более того. Поэтому здесь, как и ранее с тремя командами: O(1) + O(1) + O(1) = O(3) = O(1) отбрасываем константу и получаем: O(2n) = O(n) Помните, что любые константы в нотации О большого отбрасываются, так как О большое характеризует не конкретное время выполнения программы, а характер вычислительной сложности, ее зависимости от входных данных. По сути, все отброшенные константы связаны лишь с временем выполнения алгоритма и не имеют принципиального значения при качественном сравнении сложности алгоритмов. Правила отбрасывания константИтак, будет ли O(n) корректной оценкой сложности всей программы? Здесь перед циклом имеется еще одна команда, которая имеет сложность: O(1) Наверное, ее также следует учесть и записать итоговое выражение в виде: O(1 + n) На самом деле нет. Любая константа, которая добавляется к n, также отбрасывается и результат будет: O(n) Всегда следует помнить, что Big O – это верхняя оценка сложности алгоритма, то есть, при n стремящемся к бесконечности. И добавление к бесконечности какого-либо константного значения дает ту же бесконечность. Поэтому асимптотически верхняя граница для: O(1 + n) = O(n) И, вообще, для любой константы C можно записать: O(n + C) = O(n) Помните, Big O характеризует только скорость (динамику) роста сложности алгоритма, а не его фактическое время выполнения. В результате, получаем следующие правила отбрасывания констант: O(A∙n) = O(n)
где A, C – константы; n – размер (число) входных данных. Для лучшего понимания оценки сложности алгоритма приведу еще один пример. Распишем предыдущую программу через два цикла: lst = [1, 4, 10, -5, 0, 2, 3, ..., 18, 32] for i, x in enumerate(lst): lst[i] += 1 for x in lst: print(x) Какова сложность алгоритма с позиции Big O? Формально, можно записать так: O(1) + O(n) + O(n) = O(1 + n + n) = O(1 + 2n) И, затем, используя правила отбрасывания констант, имеем: O(1 + 2n) = O(n) Мы пришли к тому же результату, что и при оценке предыдущего варианта алгоритма через один цикл. И это логично, т.к. здесь сравнимый объем вычислений. Хотя, реальная скорость работы алгоритмов все же будет несколько отличаться. Но это, как правило, не имеет большого значения. Главное уметь оценивать принципиальные (качественные) отличия объема вычислений тех или иных алгоритмов. Как раз для этого и используется О большое. Правила сложения и умноженияНо вернемся к нашей программе и посмотрим, что будет, если перебираются два разных списка с длинами n и m: for x in range(n): print(x) for y in range(m): print(y) Вычислительная сложность алгоритма с точки зрения Big O будет равна: O(n) + O(m) = O(n + m) И никаких сокращений. Почему так? Дело в том, что теперь обе величины n и m могут принимать произвольные значения, то есть, не являются константами. Мало того, в общем случае, обе величины сравнимы между собой. Поэтому они не могут быть сокращены или отброшены. Далее, если мы один цикл запишем внутри другого: for x in range(n): for y in range(m): print(x, y) то объем вычислений в нотации О большого примет вид: O(n ∙ m) потому что обе величины n, m являются переменными и сравнимыми между собой. А умножение появляется в результате перебора m раз значений во внутреннем цикле для каждого значения x внешнего цикла. Поэтому для вложенных циклов получаем умножение, а для последовательных – сложение. Можно заметить, что здесь в частном случае, когда n = m, выходит:
ИтогиИтак, на этом первом занятии по Big O мы с вами увидели, что имеет смысл сравнивать алгоритмы по верхней границе динамики изменения их сложности в зависимости от размера n входных данных. Познакомились со следующими оценками временной сложности:
Также мы с вами увидели, что любые константы отбрасываются из нотации О большого:
И узнали, в каких случаях следует складывать объемы вычислений, а в каких умножать: На следующем занятии мы продолжим эту тему и рассмотрим примеры алгоритмов, дающих логарифмический и факториальный объем вычислений. Курс по структурам данных: https://stepik.org/a/134212 Видео по теме |