|
Хэш-таблицы. Что это такое и как работаютКурс по структурам данных: https://stepik.org/a/134212 Мы продолжаем курс по структурам данных, и на этом занятии речь пойдет о новой структуре под названием хэш-таблица. Она обладает поистине впечатляющими характеристиками. Для стандартных операций вставки, чтения и удаления данных она, в среднем, выполняется за константное время O(1), то есть, быстро и не зависимо от размера таблицы (объема данных):
И в этом она превосходит подобные ей структуры: динамические массивы и связные списки. Получается, что хэш-таблица может их полностью заменить? Но не спешите и давайте во всем подробно разберемся. Первым делом рассмотрим принцип работы хэш-таблиц. Предположим, в продуктовом магазине необходимо хранить товары и выдавать цену по их названиям.
Как это сделать? Из того, что мы знаем на данный момент, вполне подошел бы связный список, т.к. в него достаточно быстро можно добавлять новые товары и удалять ненужные. Правда, поиск будет выполняться линейное время O(n). И это нас не очень устраивает, т.к. товаров в магазине может быть очень много и нам бы хотелось иметь более быстрый доступ к цене товара по его названию. Поэтому сделаем несколько иначе. Единственная из всех рассмотренных структур, которая предоставляет быстрый доступ к элементу за время O(1) – это массивы (и динамические массивы).
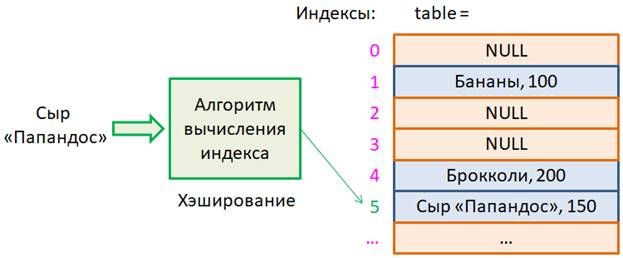
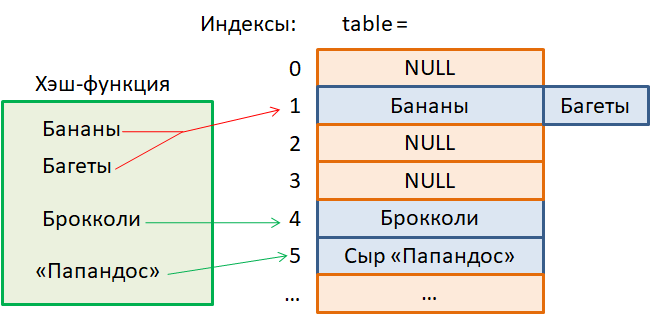
Но здесь нас ожидают сразу две проблемы: во-первых, мы знаем названия, но не индексы элементов, а значит, поиск нужного товара займет O(n) времени, и, во-вторых, операции добавления и удаления товара также потребуют O(n) времени. Получается довольно неудачный выбор структуры для данных. Но не спешите с выводами. Давайте пойдем на небольшую хитрость. Придумаем алгоритм, который бы переводил названия товаров в индексы, и тогда, мы получим возможность сразу обращаться к нужной ячейке таблицы (массива), чтобы записать его туда, прочитать оттуда, или удалить, когда это потребуется:
Так вот, алгоритм преобразования некоторой строки в индекс массива получил название хэш-функция, а процесс его работы – хэширование. Отсюда пошло название хэш-таблица. Видите, какое элегантное решение у нас получается?! Достаточно придумать алгоритм (хэш-функцию), который бы переводил названия товаров в индексы массива и все, мы имеем структуру данных с операциями записи, чтения и удаления, которые выполняются за постоянное время O(1), не зависящее от размера таблицы (массива). Но можно ли найти такую хэш-функцию в общем случае? Очевидно, она должна обладать следующими свойствами:
Как видите, имеются достаточно жесткие требования (ограничения) на алгоритм вычисления индекса (хэш-функции). Естественно, возникает вопрос, можно ли вообще построить такую функцию? Сразу отвечу, что в общем случае нет, невозможно. Хотя бы исходя из того, что количество ключей (в нашем примере – это названия товаров) может быть огромное количество K. И оно явно больше числа ячеек таблицы (размера массива) M. Поэтому мы просто не сможем всем ключам выдать уникальные индексы. Вторая проблема – это равномерность заполнения таблицы. Хорошая хэш-функция должна разные ключи как можно равномернее распределять по массиву, минимизируя, тем самым, дублирование индексов. Но обо всем этом мы еще поговорим. А пока будем полагать, что у нас уже есть алгоритм хэширования, и посмотрим на работу хэш-таблиц в целом. Добавление элементов в хэш-таблицуДавайте предположим, что мы бы хотели по английским буквам получать соответствующие аналоги русских букв. Например:
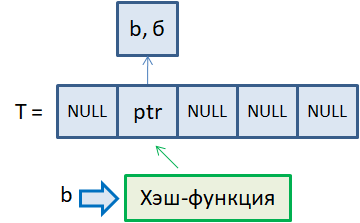
Причем нам наперед неизвестно, сколько именно букв будет храниться в хэш-таблице. Поэтому, чтобы зря не расходовать память, начальный размер таблицы будет иметь m=5 элементов. Сами ячейки таблицы будут хранить адреса на объекты с данными. Если данных нет, то указатели принимают значение NULL. Далее, у нас имеется хэш-функция, которая для каждой буквы латинского алфавита вычисляет индекс в массиве T. Предположим, мы хотим по ключу b записать значение б. На вход хэш-функции подается символ b. На выходе получаем индекс массива, по которому этот ключ должен располагаться в таблице. Пусть это будет индекс 1:
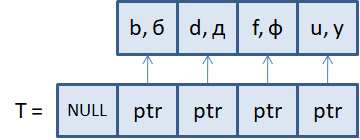
Затем, в памяти создается новый объект с ключом b и значенем б, и адрес этого объекта сохраняется во втором элементе таблицы. То есть, массив хранит не сами данные, а ссылки на объекты с данными. Это наиболее частая реализация хэш-таблиц. В результате мы добавили новый ключ b и его значение б в хэш-таблицу. На уровне языков программирования эта операция часто записывается в виде: T["b"] = "б" Разумеется, если T – это хэш-таблица. По аналогии можно добавить еще несколько ключей и значений. Например, ключи f, d, u:
И наш массив почти заполнен! В теории хэш-таблиц степень их заполненности определяется коэффициентом: α = n / m где n – количество хранимых ключей (в нашем примере 4); m – размер массива (в нашем примере 5). Получаем, значение степени заполнения таблицы: α = 4 / 5 = 0,8 То есть, пока этот коэффициент меньше единицы, в массиве есть свободные элементы, куда теоретически еще можно добавить новые ключи. Если α = 1, то массив заполнен полностью. Если же α > 1, то число ключей превышает размер хэш-таблицы. (Как такое может быть, мы еще будем говорить.) Итак, на данный момент коэффициент α = 0,8, значит, массив почти заполнен. Что делать дальше? Выход только один: увеличить размер таблицы, то есть, рассматривать массив как динамический и, например, при α близкой к 1 увеличивать его размер в 2 раза. Давайте так и сделаем. Сначала мы должны в памяти создать новый массив длиной в 2 раза больше предыдущего. После этого хэш-функция будет уже выдавать новый диапазон индексов [0; 9]. Поэтому элементы должны не просто копироваться в новый массив, а заново прогоняться через новую хэш-функцию. Получим (как пример):
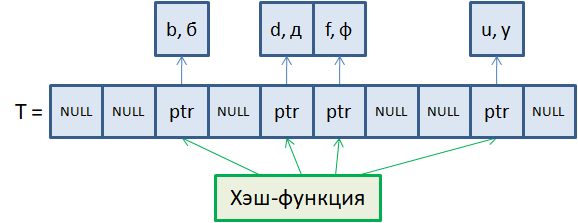
Только после этого мы сюда можем добавлять новые ключи. Вот общий принцип работы алгоритма добавления ключей и значений в хэш-таблицы. В среднем, эта операция выполняется за фиксированное время O(1). Разрешение коллизий в хэш-таблицахОднако, такая идеализированная картина, когда в одной ячейке хранится одно значение, бывает только в простых случаях, когда число ключей невелико и все их можно разнести по разным индексам. На практике же общее возможное число ключей K стремится к бесконечности, их вариации могут быть самыми разными и рано или поздно возникает ситуация, когда разным ключам хэш-функция назначает один и тот же индекс:
И избежать этого невозможно, так как алгоритмически мы должны обеспечивать не только различие в индексах, но и равномерность заполнения таблицы. Кроме того, число ячеек M в таблице много меньше возможного числа ключей. Поэтому вполне вероятны ситуации, когда разным ключам назначается один и тот же индекс. Такая ситуация называется коллизией. Спрашивается, как быть в таком случае? Существует два основных метода разрешения коллизий:
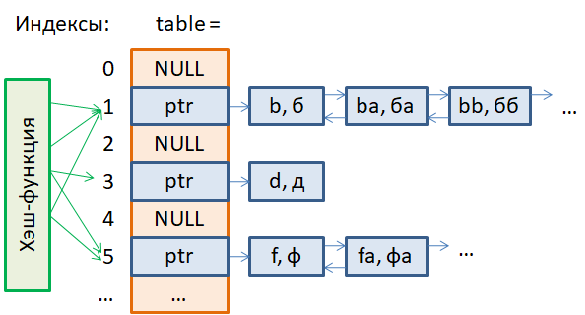
Самый простой и очевидный способ обработки коллизий – это метод цепочек. Давайте предположим, что в хэш-таблицу T осуществляется добавление следующих пар ключ-значение: T["b"] = б T["ba"] = ба T["d"] = д T["f"] = ф T["bb"] = бб T["fa"] = фа
И хэш-функция для ключей с одинаковыми первыми буквами выдает одни и те же индексы таблицы. Тогда, чтобы сохранить несколько разных ключей по одному и тому же индексу, формируется двусвязный список, на начало которого ведет указатель ptr. В элементах этого двусвязного списка сохраняются пары ключ-значение. Это и есть принцип разрешения коллизий по методу цепочек. У такого решения есть положительные и отрицательные стороны. К положительным можно отнести простоту реализации. Сформировать двусвязные списки там, где необходимо хранить несколько ключей, не составляет особого труда. Также относительно быстро происходит вставка новых ключей и удаление существующих в таких списках (цепочках). А основным недостатком является возможность появления длинных цепочек в хэш-таблицах. Тогда поиск нужного ключа может занять продолжительное время и преимущества хэш-таблиц будут сведены к нулю. Очевидно, чтобы избежать такого неблагоприятного случая (образования длинных цепочек), нужно правильно выбирать хэш-функцию, которая бы равномерно распределяла возможные ключи по индексам таблицы. Благо, существуют подходы, позволяющие создавать такие функции, но об этом мы еще будем говорить. А сейчас посмотрим, как в хэш-таблицах со списками выполняется поиск и удаление ключей. Алгоритм поиска ключейДавайте предположим, что у нас имеется ранее сформированная хэш-таблица с цепочками и в ней требуется взять значение по определенному ключу. Пусть это будет ключ «ba», то есть, нужно выполнить операцию: val = T["ba"] Для этого мы подаем ключ «ba» на вход хэш-функции, получаем значение индекса 1 в таблице и видим здесь двусвязный список. На начало этого списка ведет указатель ptr. Сформируем временный указатель: p = ptrкоторый также будет ссылаться на начало этого списка. Далее, мы последовательно проходим по элементам этого списка и сравниваем в них ключи на равенство заданного ключа «ba». Этот ключ мы находим во втором элементе списка. На этом поиск останавливается и возвращается значение "ба" этого ключа. Если мы указываем не существующий ключ, например, «t», то либо попадем в пустую ячейку таблицы, либо не найдем этот ключ в списке. Вот так, достаточно просто реализуется алгоритм поиска ключей в хэш-таблице с цепочками. Алгоритм удаления ключейДавайте теперь посмотрим, как можно выполнять удаление существующих ключей из хэш-таблицы с цепочками. У нас по-прежнему будет та же самая таблица и мы хотим удалить из нее ключ «ba»: del T["ba"] Вначале также подаем этот ключ на вход хэш-функции и получаем индекс 1 в таблице. По этому индексу хранится несколько ключей в двусвязном списке. С помощью временного указателя p находим элемент с ключом «ba». Это второй элемент. И удаляем его. (Как удалять элементы в двухсвязных списках мы с вами уже говорили на предыдущих занятиях). Все, ключ удален из хэш-таблицы. Если происходит удаление единственного ключа в ячейке, например, ключа «d», то проверяется, что в единственном элементе действительно хранится ключ «d», если так, то объект удаляется и ячейка принимает значение NULL. Наконец, если пытаемся удалить не существующий в таблице ключ, например, «s», то либо сразу попадаем в ячейку со значением NULL, либо на цепочку из ключей, в которой ключ «s» будет отсутствовать. В любом случае, при отсутствии ключа никаких действий с таблицей не выполняется и она остается в неизменном виде. ИтогиИтак, на этом занятии мы с вами в целом познакомились с концепцией хранения данных в виде хэш-таблицы. Ввели понятие хэш-функции и коллизий, когда разным ключам назначается один и тот же индекс. Разобрали метод цепочек, как один из способов разрешения коллизий. А также увидели, каким образом выполняется поиск и удаление ключей из хэш-таблицы. На следующем занятии мы продолжим эту тему и подробнее поговорим о способах выбора хэш-функций, а также разберем второй способ устранения коллизий методом открытой адресации. Курс по структурам данных: https://stepik.org/a/134212 Видео по теме | ||||||||||||||||||||||||||||||||||||||||||||||