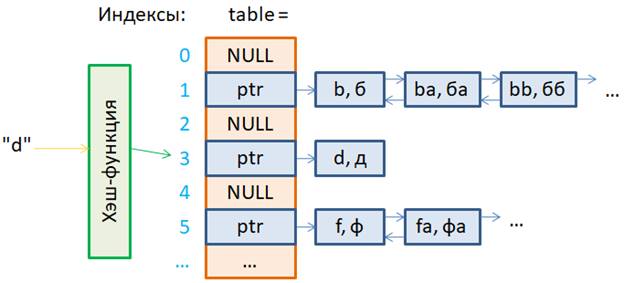
|
Хэш-функции. Универсальное хэшированиеКурс по структурам данных: https://stepik.org/a/134212 На прошлом занятии мы в целом познакомились с работой хэш-таблиц. Теперь пришло время затронуть важный вопрос, как найти хорошую хэш-функцию? И что значит слово «хорошая»? Как мы с вами уже говорили, на вход алгоритма хэширования подается некий ключ, например, «d». На выходе получаем индекс ячейки массива, куда записывается значение этого ключа:
Так вот, в качестве ключей хэш-таблиц можно использовать любую байтовую последовательность. На уровне компьютера – это она воспринимается, как конечная последовательность из целых чисел в диапазоне от 0 до 255 включительно, например (в соответствии с кодовой таблицей ASCII): "for" –
"102, 111, 114"
И так для любой байтовой последовательности. Затем, над этими числами выполняются какие-либо алгоритмические и математические операции так, чтобы свести все к одному числу k, как правило, целому и неотрицательному. После этого полученное число передается в качестве аргумента непосредственно в функцию хэширования, которая возвращает индекс массива: i = h(k) Вот основные этапы преобразования начального ключа в индекс таблицы при хэшировании. На этом занятии мы с вами сосредоточимся непосредственно на функции h(k), а ключами будем считать некие числа k. Вопрос о преобразовании последовательности байт в число я опущу. Если интересно, то об этих алгоритмах легко найти информации на просторах Интернета. Способы построения хэш-функцийДавайте теперь вернемся к вопросу, что такое хорошая хэш-функция. Как мы с вами уже говорили, она должна обладать следующими основными свойствами:
Я думаю, здесь в целом все понятно, кроме, может быть последнего свойства: зачем требовать от хэш-функции равномерного распределения ключей по ячейкам таблицы? Смотрите. В общем случае, мы наперед не знаем, какие ключи k будут подаваться на вход хэш-функции. Очевидно, что возможное количество этих ключей K много больше текущего числа ячеек M в хэш-таблице. Значит, хэш-функция h(k) отображает большее множество K в меньшее M. И как бы мы ни выбирали функцию h(k), обязательно будет существовать пара ключей k1, k2, которым функция h(k) назначит один и тот же индекс. Лучшее, что мы здесь можем сделать – это минимизировать вероятность такого события. А это, в свою очередь, приводит к равномерности распределения хэш-функцией возможных ключей {k} по ячейкам таблицы. Вот отсюда и появляется последнее требование к хорошей хэш-функции. В этом случае можно доказать, что средняя длина цепочек в хэш-таблице будет равна коэффициенту заполнения: α = n / m, где n – число хранимых ключей; m – общее число ячеек в таблице. И алгоритмы поиска/удаления ключей, в среднем, будут выполняться за: 1 + α операций. Это среднее минимальное число, которое может быть достигнуто. Построение хэш-функции методом деленияНаверное, самое простое, что мы можем сделать, чтобы преобразовать множество целых неотрицательных чисел {k} (ключи) в диапазон значений [0; m-1] (индексы таблицы) – это взять и вычислить остаток от деления операцией:
Я напомню, что в языках С++ и Python функция mod реализуется оператором % следующим образом: h(k) = k % m На выходе имеем множество целых значений в нужном нам диапазоне [0; m-1]. Получается, мы
только что построили простую и универсальную хэш-функцию, которую можно
использовать в любых хэш-таблицах? Давайте проверим, так ли это? Пусть
Смотрите, число m=16, фактически, выделяет последние 4 бита ключа k. И если вдруг так окажется, что все потенциальные ключи {k}, которые будут сохраняться в хэш-таблице, имеют одинаковые последние 4 бита, то всем им будет назначен один и тот же индекс. То есть, мы получим худший случай работы хэш-таблицы. Чтобы этого
избежать, число m следует выбирать, во-первых, простым
(то, что делится только на самого себя и на единицу), а, во-вторых, как можно
более далеким от степени двойки, то есть, от чисел Построение хэш-функции методом умноженияДругой метод умножения для построения хэш-функций решает эту проблему:
Здесь A – некоторая
константа, выбранная из диапазона 0 < A < 1 так,
чтобы при умножении k на A формировалось
дробное число, а затем, с помощью операции mod 1 выделяется
эта дробная часть числа. Благодаря этому, мы как бы перемешиваем возможные
значения ключей {k}, формируем случайные числа, зависящие от k, причем, эти
числа находятся в диапазоне [0; 1). Все что нам остается – это расширить
диапазон до [0; m-1] в целых числах. Для этого вещественное число
умножается на m с округлением
до наименьшего целого (оператор Вот
математический смысл этой формулы. В результате, число m теперь можно
выбирать любым и это никак не скажется на качестве работы хэш-функции. Часто Здесь только остается вопрос, как выбрать константу A? Дональд Кнут в своем известном труде «Искусство программирования» предложил значение этой константы брать равной:
Как показала практика, при таком значении A мультипликативная хэш-функция h(k) для произвольных ключей k дает более-менее равномерное распределение. Другие алгоритмы хэшированияВообще, как выбрать конкретный вид хэш-функции для решения той или иной задачи – вопрос открытый. Например, в практике построения хэш-таблиц также строят хэш-функции на базе известных алгоритмов из криптографии, например:
Можно предложить и другие подобные детерминированные алгоритмы, которые переводят последовательность байт (ключей) в числа с равномерным распределением. А уже потом, эти числа можно перевести в любой требуемый диапазон индексов хэш-таблицы. Универсальное хэшированиеИтак, мы увидели каким образом можно выполнять построение хэш-функций. Но как бы хорошо не работал алгоритм хэширования остается одна важная проблема: для каждой конкретной функции h(k) всегда можно подобрать такой набор ключей {k}, что все они будут располагаться в одной ячейке хэш-таблицы, то есть, для всех них функция выдаст одно и то же значение. Этим обстоятельством, например, может воспользоваться злоумышленник, чтобы специально замедлить работу программы. В любом случае, это некая уязвимость, которую хотелось бы устранить. Давайте посмотрим, как с этим можно бороться? Пусть у нас имеется несколько хеш-функций:
В целом, они по-разному распределяют одни и те же ключи по таблице. Тогда, чтобы исключить предсказуемость распределения набора ключей {k}, мы в момент создания очередной хэш-таблицы случайным образом выберем одну из хеш-функций и будем ее использовать для текущей хеш-таблицы. В этом случае, какой бы набор из ключей {k} ни подавался на вход алгоритма хеширования, он в разных таблицах будет распределяться по-разному. А это именно то, что нам и нужно. Таким образом, уязвимость будет устранена. Но как сформировать набор из H хэш-функций? Если мы будем их просто формировать по методу умножения или деления, или еще как-нибудь, то может возникнуть ситуация, когда разные хэш-функции для определенного набора ключей {k} будут выдавать схожие значения индексов. То есть, результаты работы функций окажутся не такими уж и независимыми. И тогда злоумышленник снова может воспользоваться своей идеей и подать на вход алгоритма хэширования проблемный набор ключей. Поэтому мало сформировать множество разных хэш-функций, они должны еще выдавать независимый набор индексов для одного и того же набора входных значений {k}. Именно такой набор функций получил название универсального. Итак, нам нужно построить универсальный набор хэш-функций, чтобы устранить проблему предсказуемости распределения ключей по индексам таблицы. Как это сделать? Томас Кормен в книге «Алгоритмы: построение и анализ» описывает следующий математический подход. Универсальное множество хэш-функций можно построить по правилу:
где p – некоторое
простое число, которое больше размера таблицы m;
различных
хэш-функций. Причем значение m выбирается произвольным образом, то
есть, размер хэш-таблицы может быть любым, в том числе и Далее,
доказывается, что для двух случайных ключей Таким образом, если мы хотим реализовать универсальное хэширование, то достаточно определить простое число p > m, а затем, случайным образом выбрать значения a и b из их диапазонов. Эти значения определяют конкретный вид хэш-функции, которая используется для перевода ключей в индексы таблицы. В результате, злоумышленник не сможет наперед знать, какая именно будет использована хэш-функция, а значит, не сможет подготовить проблемный набор ключей {k} для образования длинных цепочек в хэш-таблице. В этом и состоит идея универсального хэширования. Курс по структурам данных: https://stepik.org/a/134212 Видео по теме |
,
где p – некоторое
натуральное число, например, 
. В
итоге, для разных ключей получим следующее распределение:
. Но
это, в свою очередь, накладывает определенные ограничения на размер m таблицы, что не очень
удобно, так как размер хэш-таблицы может меняться по мере ее заполнения.
).
, 
-
целые числа, взятые из указанного диапазона. В результате, всего мы имеем:
,
где n – натуральное
число.
любая
выбранная хэш-функция выдаст одно и то же значение (индекс) с вероятностью 1/m, где m – размер хэш-таблицы.
То есть, ключи распределяются равномерно.
