|
Бинарные деревья. НачалоКурс по структурам данных: https://stepik.org/a/134212 На этом занятии мы затронем новую тему – бинарные деревья. Что это такое? Давайте предположим, что нам в программе нужно хранить и обрабатывать иерархические структуры данных, например, генеалогическое древо семьи, или структура каталогов и файлов и т.п.
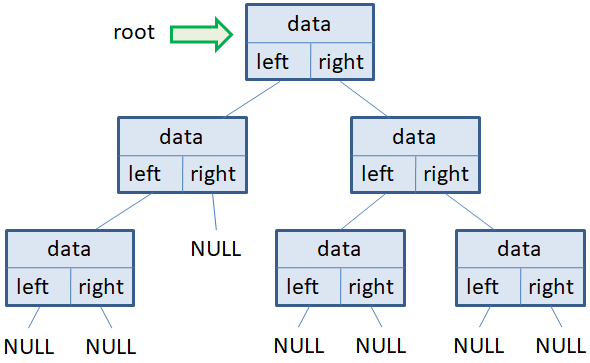
То есть, везде, где есть некая начальная (корневая) вершина, от которой можно провести связи к дочерним, а от них – к следующим дочерним, получается иерархическая древовидная структура. Именно о таких структурах данных мы и будем вести речь на ближайших занятиях. Начальная вершина дерева, от которого следуют все остальные, называется корнем дерева (root). Сами элементы дерева – узлами или вершинами (nodes). Причем, узел слева, называется левым, а справа – правым. Если у вершины нет левого или правого потомка, то обычно указывают значение NULL. Вершины, у которых нет потомков, называются листьями. Само же дерево, у которого каждая вершина может содержать не более двух дочерних узлов, называется бинарным или двоичным. Всю эту терминологию и обозначения, мы в дальнейшем будем активно использовать. Структура бинарного дереваЧаще всего в практике программирования используют бинарные деревья. Даже когда у вершины предполагается множество потомков, то зачастую задачу сводят все равно к бинарным деревьям или какой-либо другой структуре данных. Поэтому мы в рамках данного курса ограничимся именно бинарными деревьями. Каждая вершина такого дерева содержит, как минимум, три поля:
Иногда еще добавляют ссылку на родительский узел. Но чаще всего ограничиваются этими тремя полями. На вершину дерева, которая называется корнем, ведет указатель root. И через этот указатель происходит вся работа с бинарным деревом: добавление/удаление элементов; обход всех узлов дерева. То есть, из корневого узла можно пройти до любого другого в данном дереве. При этом, количество вершин, через которые нужно пройти, чтобы достичь некоторого узла, определяет уровень (level) дерева. Если дерево не содержит ни одной вершины, то root = NULL. Также, если у какой-либо вершины отсутствует левый или правый потомок, то соответствующий указатель принимает значение NULL. Добавление вершин в бинарное деревоДавайте теперь посмотрим, как можно формировать бинарное дерево, то есть, добавлять в него новые вершины. Обычно, новые узлы добавляются к свободному указателю (то есть, тот, который принимает значение NULL), начиная с корневого. То есть, первая вершина всегда добавляется в корень, и других вариантов просто нет. А вот далее, мы уже решаем добавить левый или правый узел. Строго говоря, ограничений здесь никаких нет. Алгоритм добавления может быть самым разным, исходя из поставленной задачи. Например, если нам нужно сформировать генеалогическое древо, то, очевидно, в вершинах последовательно должны указываться потомки: на нулевом уровне – некоторый человек; на первом – мама, папа; на втором – бабушки, дедушки и т.д. Но есть отдельный класс задач, когда в вершинах бинарного дерева хранятся данные, которые можно сравнивать на больше и меньше (например, числа), и добавление нового узла происходит по правилам:
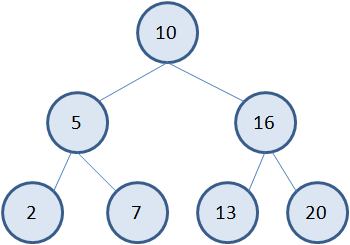
Например, предположим, мы собираемся хранить в вершинах бинарного дерева целые числа. И будем последовательно добавлять узлы для значений: 10, 5, 7, 16, 13, 2, 20 Первое значение 10 просто добавляется в корневую вершину. Следующее значение 5. Смотрим от корня. Пять меньше 10. Тогда, согласно нашим правилам, это значение нужно записать в левую ветвь. Формируем новый узел со значением 5. Следующее значение 7. Снова идет от корня дерева. Семь меньше 10, переходим в левую ветвь. Здесь у нас узел со значением 5. И пять больше 7. Следовательно, семь нужно добавить в качестве правого узла дерева у вершины 5. Далее, идет число 16. Оно больше 10, поэтому добавляем его в качестве правой вершины у корневой. Затем, число 13. Оно также больше 10, но меньше 16. Следовательно, нужно добавить левый узел у вершины 16. Следующее значение 2 меньше 10 и меньше 5. Добавляем новый узел справа от узла 5. И последнее значение 20 – самое большое, поэтому оно станет самой крайней правой вершиной дерева.
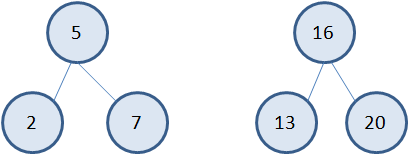
Благодаря такому подходу в формировании бинарного дерева, у нас в левой ветви будут находиться вершины со значениями меньше, чем у корневой, а в правой ветви – вершины со значениями больше корневой. И этот вывод будет справедлив для любого выделенного фрагмента поддерева, например:
Поиск значений в бинарном деревеХорошо, но что нам это дает? Смотрите, здесь появляется несколько интересных эффектов. Первый – это ускорение поиска заданного значения. Например, нам нужно определить, находится ли число 2 в последовательности чисел 10, 5, 7, 16, 13, 2, 20. Если бы мы хранили числа в обычном массиве:
то время поиска, с точки зрения O большого, составило бы O(n), где n – число элементов в массиве. Нам пришлось бы последовательно перебирать все элементы и сравнивать значения с числом 2. А вот в бинарном
дереве все несколько иначе и, в среднем, быстрее. Вначале число 2 сравнивается
с числом 10. Оно меньше, поэтому идем по левой ветви, где сосредоточены вершины
со значениями меньше 10. В результате, мы сразу отсекаем правую группу
элементов, значения которых заведомо не равны 2. За счет этого происходит
ускорение поиска. Затем, сравниваем 2 и 5. И, так как 2 меньше 5, то снова
переходим по левой ветви. Находим заданное значение. Как видите, нам
потребовалось всего три сравнения, чтобы найти число 2 в бинарном дереве. С
позиции О большого среднее число операций, необходимое для поиска нужного значения
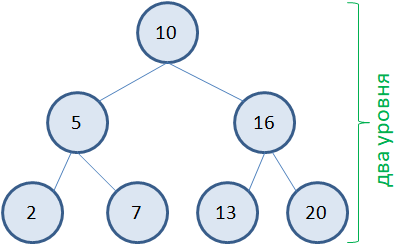
составляет Давайте теперь посмотрим на работу алгоритма в случае, когда заданное значение для поиска в бинарном дереве отсутствует. Например, это число 11. Очевидно, мы должны идти сначала по правой ветви, в узле 16 – по левой, и доходим до листовой вершины 13. Далее, никаких узлов в дереве нет, но значение не было найдено, следовательно, в дереве нет этого числа 11. Или, такой пример. Нам нужно найти число 5. Оно хранится в промежуточной вершине. Поэтому, когда мы доходим до нее, то дальнейший процесс поиска прерывается, значение найдено. Вот принцип, по которому выполняется поиск значений в вершинах бинарного дерева. Сбалансированные и несбалансированные деревьяВнимательный зритель сейчас мог бы мне возразить и сказать, что у нас все так хорошо получается, потому что я привел пример «красивого» бинарного дерева с минимальным числом уровней (всего два):
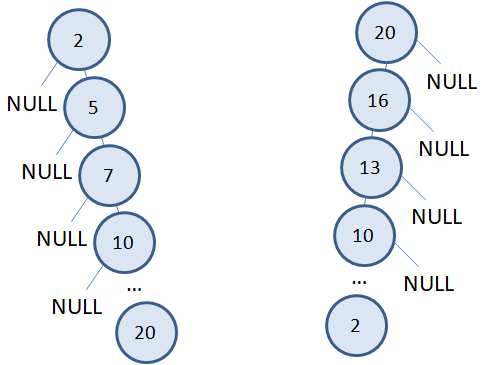
Но, если бы числа при формировании дерева поступали в другом порядке, или по возрастанию: 2, 5, 7, 10, 13, 16, 20 или по убыванию: 20, 16, 13, 10, 7, 5, 2 то деревья выглядели бы совсем иначе:
Фактически, они вырождаются в односвязный список и объем вычислений для поиска заданного значения в них составляет O(n). Так же, как и в обычных массивах или связных списках. Выигрыша уже нет. Такие вырожденные деревья (и подобные им) называются несбалансированными. В отличие от первого, которое относится к сбалансированным. Вообще, дерево называется сбалансированным, если в нем поддеревья от одной вершины отличаются не более чем на один уровень. И именно в сбалансированных деревьях поиск значений в вершинах выполняется за минимальное число шагов с объемом вычислений O(log n). Поэтому, на практике, стремятся строить деревья близкие к сбалансированным. Для этого используют методы балансировки двоичных деревьев, среди которых, наиболее известны следующие:
Любой из этих методов может быть реализован в бинарном дереве и вызываться при добавлении новых вершин. В результате получаем более сбалансированное дерево при любых входных последовательностях данных. В данном курсе мы не будем углубляться в эти темы. Кому будет интересно, подробную информацию по этим методам легко найти на просторах Интернета. Отмечу только, что если нам известно, что в решаемой задаче данные (значения) поступают в случайном порядке, то в среднем, будет формироваться бинарное дерево близкое к сбалансированному. На этом мы завершим наше первое знакомство с бинарными деревьями, а на следующем продолжим и поговорим об алгоритмах обхода и удаления вершин бинарных деревьев. Курс по структурам данных: https://stepik.org/a/134212 Видео по теме |