|
Бинарное дерево. Способы обхода и удаления вершинКурс по структурам данных: https://stepik.org/a/134212 Мы продолжаем тему по бинарным деревьям. На этом занятии детально рассмотрим способы обхода вершин бинарного дерева. Существует два основных подхода:
При обходе в ширину, перебор узлов дерева выполняется по уровням слева направо. При обходе в глубину сначала доходят до листовой вершины, а затем, переходят к следующей ветви. Давайте детальнее разберем эти алгоритмы. Алгоритм обхода в ширинуДавайте представим, что у нас имеется следующее двухуровневое бинарное дерево:
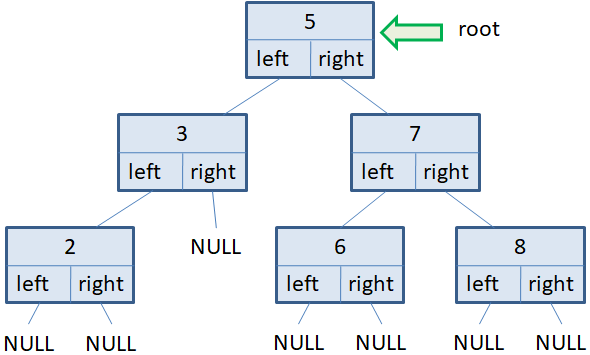
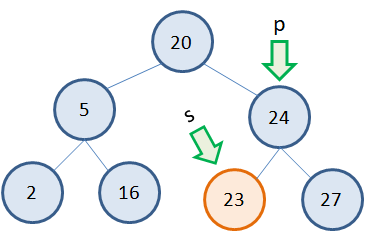
На корневую вершину ведет указатель root. Создадим еще один вспомогательный указатель p на эту же вершину: p = rootи список из вершин текущего уровня в порядке слева-направо: v = [p] Изначально в списке только одна корневая вершина. Сформируем два цикла: первый будет работать, пока список вершин не пуст, то есть, пока в дереве имеются узлы текущего уровня; а второй будет перебирать вершины текущего уровня, выводить информацию на экран и формировать список следующего уровня: while v: vn = [] for x in v: print(x.data) if x.left: vn += [x.left] if x.right: vn += [x.right] v = vn В результате, сначала будет выведено значение 7 корневого узла. Затем, сформирован список vn из двух узлов следующего уровня в порядке слева-направо. После этого списку v присваивается новый сформированный список vn следующего уровня и на следующей итерации цикла while во вложенном цикле for будут перебираться уже вершины первого уровня. На экран выведутся значения 2 и 5. Снова сформируется список vn из вершин следующего второго уровня. И на следующей итерации цикла while будут выведены значения 3, 4 и 6. После этого список vn окажется пустым, следовательно, список v также будет пустой и цикл while завершит свою работу. Вот пример реализации алгоритма перебора вершин бинарного дерева в ширину в самом простом варианте. При этом мы обходим по всем узлам дерева ровно один раз. Алгоритм обхода в глубинуСледующий тип алгоритмов – это обход дерева в глубину. Здесь мы проходим по определенной ветви до листовой вершины. Лучше всего показать этот ход на конкретном примере. Пусть у нас то же самое бинарное дерево. Начальная вершина, как всегда, корневая (root). Затем, мы должны для себя решить, по какой из двух ветвей идти в первую очередь, а по какой – во вторую. Я решил обойти дерево сначала по левой ветви, а затем, с возвратами проходить правые ветви. Это можно реализовать следующей рекурсивной функцией: def show_tree(self, node): if node is None: return self.show_tree(node.left) print(node.data) self.show_tree(node.right) С начальным вызовом от корневой вершины: show_tree(root) Как она работает? Мы начинаем двигаться от корневого узла. Если он существует, то вызывается та же самая функция для левого узла. В результате, мы как бы попадаем в ту же самую функцию, только параметр node теперь является ссылкой на узел со значением 3. Здесь выполняется та же самая проверка: если узел существует, то по рекурсии мы снова переходим к следующему левому узлу. Это узел со значением 2. Снова делается проверка на его существование и, так как он существует, переходим к следующему левому узлу. Теперь параметр node принимает значение None (на рисунке NULL), рекурсия завершается и мы возвращаемся к прежнему вызову с параметром node узла 2. Это значение отображается на экране и делается попытка пройти по правой ветви. Так как справа объектов нет, то вызов текущей функции завершается и мы попадаем в функцию уровнем выше с параметром node на узел 3. Это значение 3 выводится на экран и делается попытка пройти по правой ветви. Ее нет, поэтому мы возвращаемся на уровень выше, то есть, к корневому узлу со значением 5. Это значение выводится на экран и далее мы переходим к правой вершине 7. Снова вызывается рекурсивная функция с параметром node на узел 7 и делается попытка пройти по левой ветви. Там имеется вершина со значение 6. Она выводится на экран с возвратом к функции узла 7. Затем, отображаем эту семерку на экран и переходит к левому узлу со значением 8. Это значение также отображается, после чего все вызовы рекурсивных функций завершаются. В результате мы на экране увидим следующие значения, записанные в вершинах бинарного дерева: 2, 3, 5, 6, 7, 8 Вы можете подумать, что такой возрастающий порядок значений получился чисто случайно. Однако нет. Если у нас имеется бинарное дерево сформированное по правилу добавления меньших значений в левую ветвь, а больших – в правую, то при обходе дерева в глубину в порядке: левое поддерево (L); промежуточная вершина (N); правое поддерево (R) всегда будет образовываться возрастающая последовательность чисел. Сокращенно такой алгоритм в глубину получил название LNR и относится к симметричному типу обхода. А если пройти сначала по правой ветви, затем вывести значение промежуточной вершины, а после пройти по левой ветви, то получим убывающую последовательность значений в бинарном дереве: 8, 7, 6, 5, 3, 2 Такой алгоритм сокращенно называется RNL и также является одним из видов симметричного обхода. Комбинируя различные варианты обхода и отображения значений вершин можно получать самые разнообразные вариации алгоритмов обхода в глубину. Удаление вершин бинарного дереваТеперь, когда мы с вами подробно разобрались в способах формирования бинарного дерева и алгоритмами обхода его вершин, остался один важный вопрос, связанный с удалением его узлов. Здесь возможны несколько типовых исходов. Удаление листовых вершинСамый простой случай, когда удаляется листовой узел дерева. Предположим, что это узел 23:
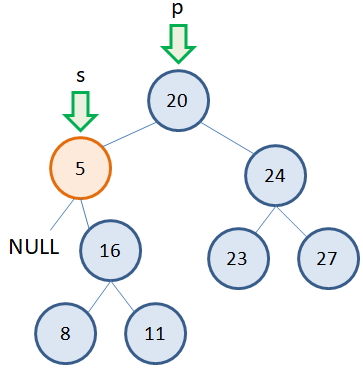
Тогда, нам достаточно получить указатель p на родительский узел и указатель s на удаляемый узел. Сделать это очень просто, запоминая при обходе дерева предыдущую (родительскую) вершину и текущую. После этого ссылку, ведущую на удаляемый узел следует приравнять NULL и освободить память из под узла s: p.left = NULL delete s Все, листовой узел удален. Как видите, все достаточно просто. Удаление узла с одним потомкомТакже относительно просто обстоит ситуация, когда у удаляемого узла имеется один потомок (слева или справа). Например, нам нужно удалить узел 5, у которого один потомок справа:
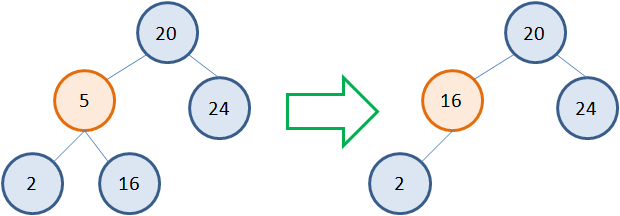
Здесь мы также должны иметь два указателя: p – на родительскую вершину; s – на удаляемую вершину. Затем, исключаем из дерева удаляемую вершину 5, меняя связь от родительской вершины 20 к вершине 16 (которая идет после удаляемой): p.left = s.right delete s Причем, ситуация принципиально не меняется, если у удаляемой вершины один правый или левый потомок. Алгоритм удаления таких вершин работает похожим образом. Удаление узла с двумя потомкамиНесколько сложнее обстоит дело, когда у удаляемой вершины два потомка. Общая идея здесь такая. Сам узел не удаляется, меняется только его значение на новое. А новое берется как наименьшее из правой ветви. Например, если мы хотим удалить узел 5, то следует взять наименьшее значение 16 из правого поддерева. Записать его вместо 5, а листовой узел 16 просто удалить:
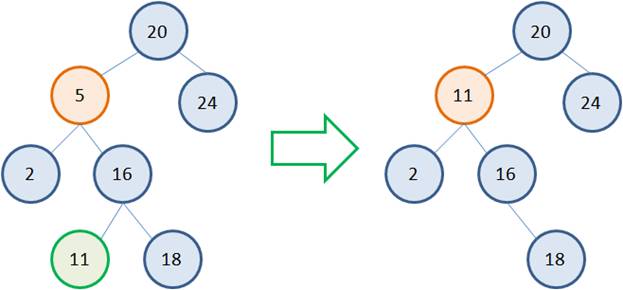
Но это если справа расположен листовой узел. А что если справа имеется полноценное поддерево с множеством вершин? Как быть в такой ситуации? По сути, также. Идея алгоритма остается прежней. Выбираем узел с наименьшим значением 11 в правом поддереве, заменяем 5 на 11 и удаляем листовой узел 11:
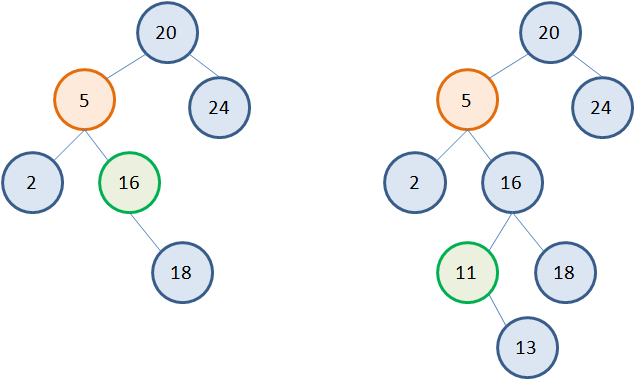
Но вершина с наименьшим значением в правом поддереве не всегда является листовой. Возможны и такие ситуации:
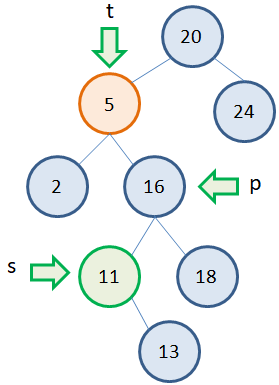
Однако можно заметить, что у узла с наименьшим значением может быть только один потомок справа. А значит, его удаление будет выполняться по алгоритму удаления вершин с одним потомком. Например, рассмотрим второе дерево. Нам потребуется три указателя: t – на удаляемую вершину (то есть, вершину, у которой будет меняться значение); s – на вершину с наименьшим значением в правом поддереве; p – на родительскую вершину для вершины s:
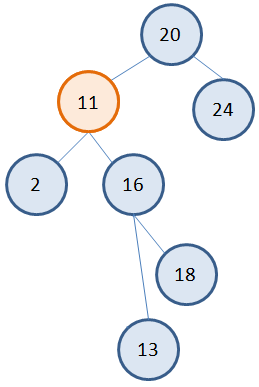
Затем, мы меняем значение вершины 5 на 11: t.data = s.data и производим удаление вершины 11 согласно алгоритму удаления вершин с одним потомком: p.left = s.right delete s В результате получаем дерево:
Вот основные типовые варианты удаления вершин в бинарном дереве:
На следующем занятии, в качестве примера, реализуем бинарное дерево на языке Python, чтобы вы во всех деталях понимали принцип его работы. Курс по структурам данных: https://stepik.org/a/134212 Видео по теме |