|
Рекурсивные функцииКурс по Python: https://stepik.org/course/100707 На этом занятии речь пойдет о рекурсивных функциях. То есть, о функциях, которые вызывают сами себя. На первый взгляд может показаться невероятным, что функция может вызывать саму себя. Но это так. И, кстати, так можно делать во всех современных языках программирования, а не только в Python. Поэтому, изучая рекурсивные функции, вы, фактически, знакомитесь с фундаментальным материалом, который применим и в других языках программирования. Чтобы все было предельно понятно, я вначале приведу фрагмент программы с набором из трех разных функций, которые вызываются друг из друга, а затем мы их заменим на одну рекурсивную функцию. Функции будут очень простыми: def rcs3(x): print(f"down: x = {x}") print(f"up: x = {x}") def rcs2(x): print(f"down: x = {x}") rcs3(x-1) print(f"up: x = {x}") def rcs1(x): print(f"down: x = {x}") rcs2(x-1) print(f"up: x = {x}") После этого вызовем функцию rcs1 с аргументом x=3: rcs1(3) В результате на экране увидим строчки: down: x = 3
Я думаю, вы без особого труда поймете, как работает эта простая программа. Вначале вызывается первая функция rcs1 с параметром x=3. В ней выполняется первая команда print с выводом первой строчки на экран. Затем управление передается следующей функции rcs2, но с параметром x=2. Она, в свою очередь, отображает следующую строчку и вызывает еще одну функцию rcs3 с параметром x=1. Эта последняя функция печатает две строчки: down: x = 1
Что происходит дальше? А дальше управление передается предыдущей функции rcs2, из которой была вызвана функция rcs3. При этом функция rcs2 продолжает свою работу, отрабатывает функция print с выводом строки: up: x = 2 После этого она завершается и управление передается функции rcs1, которая так же продолжает выполнять команды. Отрабатывает print с выводом строки: up: x = 3
На этом блок из последовательного вызова функций завершает свою работу. Все это вы уже должны хорошо знать и понимать. А вот следующий шаг будет новым. Мы заменим все эти три функции одной рекурсивной, которая будет выглядеть следующим образом: def rcs(x): print(f"down: x = {x}") if x > 1: rcs(x-1) print(f"up: x = {x}") Давайте ее вызовем с начальным значением x=3 и посмотрим, что получится: rcs(3) После запуска программы в консоли появятся те же самые строчки: down: x = 3
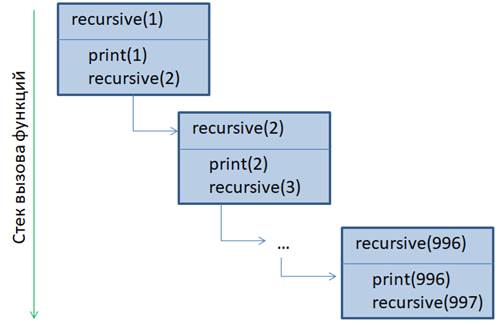
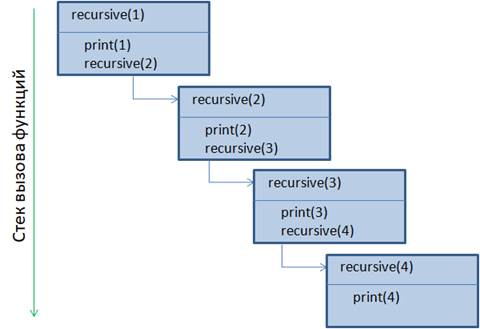
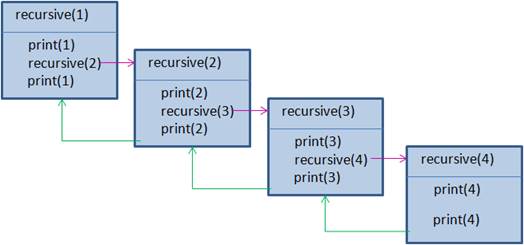
Почему получился такой результат и как это работает? На самом деле все предельно просто. Вся эта магия получается благодаря тому, что интерпретатор языка Python запоминает порядок вызова функций, то есть, какая функция из какой и с какими аргументами была вызвана. Поэтому работу нашей рекурсивной функции можно представить в виде следующих последовательных вложенных вызовов:
Все начинается с первого вызова функции rcs с аргументом x=3. В теле этой функции срабатывает print с выводом в консоль первой строчки: down: x = 3 Затем проверяется условие, что x должен быть меньше 1. Так как x=3, то условие срабатывает и снова вызывается функция rcs, но уже с аргументом x=2. Вот этот момент самый главный. Когда функция вызывает какую-либо другую функцию (в том числе и саму себя), то вызов первой функции не завершается, она продолжает работать, но появляется еще один вызов точно такой же функции, только с аргументом x=2. Для Python – это независимо работающие функции. Параметр x второй функции rcs никак не связан с параметром x первой функции rcs. Это как бы независимые копии одной и той же функции. Это ключевой момент в понимании работы рекурсивных функций: первая функция не завершается, и последующие вызовы этой же функции работают совершенно независимо друг от друга, так, словно это разные функции. Итак, мы вызвали (рекурсивно) функцию rcs с аргументом x=2. В ней снова отрабатывает print с выводом строки: down: x = 2 и проверяется условие, что x должен быть меньше 1. Условие истинно, поэтому еще раз вызывается рекурсивно функция rcs, но с аргументом x=1. Опять отрабатывает print с выводом строки: down: x = 1 А вот условие теперь оказывается ложным, т.к. один не меньше одного. В результате очередного рекурсивного вызова функции rcs не происходит. Выполнение переходит к следующей функции print с выводом строки: up: x = 1 На этом работа функции rcs(1) завершается и управление передается предыдущей функции rcs(2). Но в этой функции первые две строчки уже были выполнены, поэтому выполняется следующая с вызовом функции print, которая выводит на экран строчку: up: x = 2 На этом функция rcs(2) также завершает свою работу. Управление переходит к первой функции rcs(1) и здесь выводится строчка: up: x = 3 Вот общий принцип работы рекурсивных функций. Как видите, все предельно просто. При этом, когда движение идет вглубь, то имеем прямой ход рекурсии, а при возврате – обратный ход. Максимальное число вызовов рекурсивной функции называют глубиной рекурсии. А что будет, если глубину ничем не ограничивать? Функция будет вызываться до бесконечности? Давайте проверим. Изменим рекурсивную функцию: def rcs(x): print(f"down: x = {x}") rcs(x + 1) И вызовем ее с начальным значением x=1: rcs(1) Смотрите, функция была вызвана 997 раз, после чего возникла ошибка RecursionError – достигнута максимальная глубина рекурсии. То есть, максимальная глубина последовательного вызова функций ограничена. В действительности это ограничение есть во всех ЯП и бесконечно вызывать функции друг из друга не допустимо. Поэтому при описании рекурсивной функции нужно гарантировать ограничение ее глубины вызовов. На практике считается нормальной глубина в 10-20 последовательных вызовов. Максимум следует делать не более 100 вызовов. Если же алгоритм предполагает большие значения глубины рекурсии, то такую программу следует пересмотреть и реализовать другим алгоритмом. Примеры использования рекурсивных функцийНадеюсь, общий принцип работы рекурсивных функций вам понятен. И, возможно, остается один важный вопрос, зачем они нужны и где имеет смысл их применять? Давайте для этого рассмотрим задачу близкую к реальной. Предположим, у нас есть некоторое игровое поле pole размером 5х5 клеток и в каждой клетке проставлен либо символ ‘#’, либо символ ‘*’. Наша задача заменить связанную область из звездочек символами ‘@’:
Эту задачу достаточно просто можно реализовать с помощью рекурсивной функции, например, так: def set_zeros(p, i, j, sz): if p[i][j] != '*': return p[i][j] = '@' if i-1 >= 0 and p[i-1][j] == '*': set_zeros(p, i-1, j, sz) if i+1 < sz and p[i+1][j] == '*': set_zeros(p, i+1, j, sz) if j-1 >= 0 and p[i][j-1] == '*': set_zeros(p, i, j-1, sz) if j+1 < sz and p[i][j+1] == '*': set_zeros(p, i, j+1, sz) pole = [ ['#', '*', '*', '*', '#'], ['#', '#', '#', '#', '#'], ['*', '*', '*', '*', '#'], ['#', '#', '*', '*', '*'], ['#', '#', '*', '#', '#'], ] N = len(pole) set_zeros(pole, 2, 2, N) print(*pole, sep='\n') Здесь рекурсивная функция set_zeros() заменяет символы ‘*’ связанной области на символы ‘@’. Работает она очень просто. Вначале мы передаем ей двумерный список pole и индексы начальной клетки. Если текущая клетка списка содержит ‘*’, то она заменяется на символ ‘@’ и запускается рекурсия во все соседние клетки:
Если в соседних клетках также будет символ ‘*’, то они заменятся на символ ‘@’, и рекурсия продолжится дальше. И так, пока вся группа связанных клеток из звездочек не будет заменена символами ‘@’. После запуска программы увидим следующий результат: ['#',
'*', '*', '*', '#']
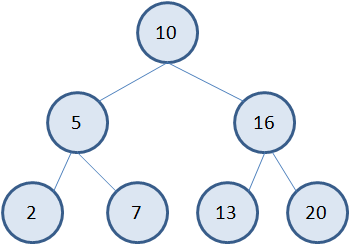
Как видите, все связанные клетки с центральной клеткой (2, 2) были заменены на символ ‘@’. Вообще рекурсивные функции очень удобны, когда нам нужно перебирать некие иерархические данные, которые имеют сложную структуру, и обычными циклами их проходить было бы затруднительно. В частности, рекурсия используется для переборов вершин бинарных деревьев – довольно распространенной структуры данных следующего вида:
Или для перебора каталогов и файлов:
И так далее. Везде, где присутствует иерархичность можно подумать об использовании рекурсивных функций. Но нужно всегда помнить и об их недостатках. Они следующие:
Курс по Python: https://stepik.org/course/100707 Видео по теме |