|
Расширенное представление чисел. Системы счисленияКурс по Python: https://stepik.org/course/100707 На этом занятии мы поговорим о различных форматах представления чисел в Python. Мы с вами неоднократно записывали в программе целые и вещественные значения в виде: a = 500 b = 0.01 Это классическая запись. Еще существует экспоненциальная, когда числа записываются через степень десятки. Например, число: 500 = 5e2 Здесь e2 – это 10 в квадрате, то есть, 100 и оно умножается на 5, получаем 500. Причем, обратите внимание, число 500 представляется как вещественное, а не целое. Аналогичным образом можно задать и второе значение 0,01 как: 0.01 = 1e-2 Здесь e-2 – это 10 в минус второй степени, то есть, 0,01 и все умножается на 1. Причем, единичка вначале строго обязательна – это формат записи чисел: сначала идет число, которое умножается на степень десятки. Зачем это может понадобиться? Часто в инженерных задачах оперируют очень большими или очень малыми числами. Например, мы хотим указать шаг сходимости градиентного алгоритма как 10^-8. Записывать это число в классическом виде: 0,00000001 не очень удобно, да и легко ошибиться в количестве нулей. А вот в экспоненциальной форме все очень удобно и наглядно: 1e-8 И то же самое с очень большими числами, например, число Авогадро (примерно): 6,02 * 10^23 = 6.02e23 Прописывать такое число в классическом виде было бы совсем уж неудобно. Причем, вначале указано вещественное число 6,02, а затем, степень десятки. Так тоже можно делать. Думаю, вы теперь знаете и сможете применять в своих программах экспоненциальную запись для чисел. Далее, мы с вами посмотрим, как можно представлять числа не только в десятичном формате, как это делали до сих пор, но и в других системах счисления: двоичной, шестнадцатеричной, восьмеричной. На самом деле их бесконечно много, так как можно придумать любую свою систему, скажем 132-ричную или еще какую, но на практике в 99% случаях ограничиваются именно такими. Вкратце я напомню, что в десятичной системе счисления все цифры умножаются на степени десяток, в зависимости от позиции их написания. Например: 123 = 1*10^2 + 2*10^1 + 3*10^0 При этом, нам достаточно иметь десять различных цифр для представления любого числа. Если же переходим к двоичной системе счисления, что все числа кодируются двумя символами: 0 и 1 – это все цифры двоичной системы (они называются битами). В результате, получаем, например, такие записи чисел в этой системе счисления: 001 = 0*2^2 + 0*2^1 + 1*2^0 = 1
Я здесь сразу привел их перевод в десятичную систему счисления, учитывая, что все позиции цифр – это соответствующие степени двойки. Так вот, в Python мы можем записывать числа непосредственно в двоичной системе, следующим образом: a = 0b001 b = 0b1101 c = 0b10001101 Причем, все числа получаются целыми. Если нужно определить отрицательное значение в двоичной записи, то проще всего перед его определением поставить унарный минус: d = -0b1111 Конечно, первая реакция человека, впервые столкнувшегося с двоичным представлением чисел, зачем это нужно? Куда привычнее использовать десятичную запись. Да, и часто именно ее применяют. Но бывают ситуации, например, работа с числами на уровне бит, когда нам требуется включить или выключить отдельный бит числа, или проверить является ли текущий бит равным 1 (то есть включенным) или 0 (выключенным). Здесь двоичное представление нам помогает визуализировать такой процесс. Следующая часто используемая система счисления – шестнадцатеричная. Здесь уже используется 16 различных обозначений. Для этого берут десять цифр из десятичной системы и еще первые шесть букв латинского алфавита: 0-9, A, B, C, D, E, F Числа принимают уже такой вид: 1A, FB, C2DE и т.п. Для перевода их в привычную нам десятичную систему, используется тот же принцип. Распишем их в виде: 1A = 1*16^1 + A*16^0 = 26
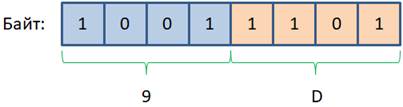
Здесь буква A соответствует значению 10 в десятичной системе, поэтому получаем значение 26. Буква F = 15, B = 11, поэтому имеем значение 251. А последнее число расшифруйте самостоятельно, должно получиться значение 49886. В чем ценность шестнадцатеричной системы счисления? Она получила широкое распространение благодаря удобному представлению байтовых данных. Один байт – это восемь бит. Если разделить байт на две части, то получим по четыре бита. В эти четыре бита можно записать одно из шестнадцати значений, то есть, одно из значений шестнадцатеричной системы счисления: 0 – F Получается, что два символа шестнадцатеричной системы, как раз описывают один байт. Причем, делают это независимо друг от друга.
При определенной тренировке, глядя на шестнадцатеричную запись, мы легко можем ее перевести и в десятичную и в двоичную системы. В Python можно записывать числа сразу в шестнадцатеричной системе, например: a = 0x1A Причем, можно использовать не только заглавные, но и малые латинские буквы: b = 0xde c = 0xaa3f Везде получаем целые положительные значения. Для определения отрицательных чисел можно вначале указать унарный минус: d = -0x342 Последняя восьмеричная система, которую мы рассмотрим, работает по аналогии с предыдущими, только используется основания для восьмерки. Соответственно, для определения чисел достаточно восемь различных обозначений – используют первые восемь цифр десятичной системы. Сами числа записываются в виде: 27
= 2*8^1 + 7*8^0 = 23
Здесь я сразу перевел их в десятичный вид. Если нам нужно определить число в восьмеричной системе, то в Python используется следующая запись: a = 0o27 b = 0o54 c = -0o775 Вот такие базовые системы счисления можно использовать в Python для определения чисел, а также применять экспоненциальную форму их представления. Курс по Python: https://stepik.org/course/100707 Видео по теме |