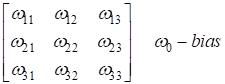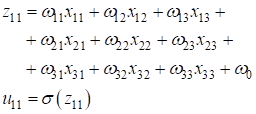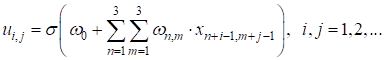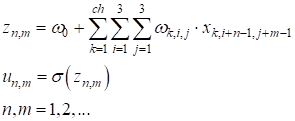|
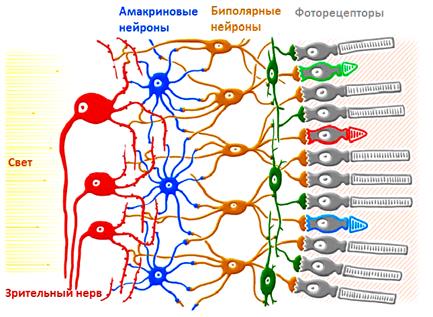
Введение в сверточные нейронные сети CNNКурс по нейронным сетям: https://stepik.org/a/227582 Вы наверняка слышали, что НС способны решать задачи классификации графических образов (отличать кошку от собаки, самолет от автомобиля, мужчин от женщин и т.д.), делать стилизацию изображений, выполнять их раскраску, генерировать новые графические образы и делать много других интересных вещей с изображениями. И мы с вами научимся делать некоторые из этих эффектов. Так вот, когда речь заходит об обработке изображений, то используется особая архитектура НС – сверточные НС. По-английски звучит как: Convolutional Neural Networks (CNN) Изначально они были предложены Яном Лекуном и спроектированы для задач классификации графических образов. Но их восхождение началось с того, что в 2012-м году команда Алекса Крижевски выиграла в ежегодном соревновании ImageNet по распознаванию графических образов. Их алгоритм показал точность в 83,6% правильной классификации – рекорд того времени. И этот рекорд был достигнут сверточной НС – AlexNet. Общая идея архитектуры таких сетей была подсмотрена у биологической зрительной системы. Ученые выяснили, что дендриды каждого нейрона соединяются не со всеми рецепторами сетчатки глаза, а лишь с некоторой локальной областью. И уже дендриды всей группы зрительных нейронов покрывают сетчатку глаза целиком:
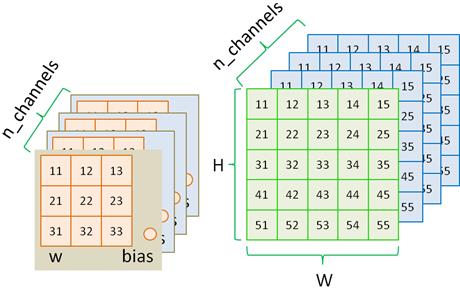
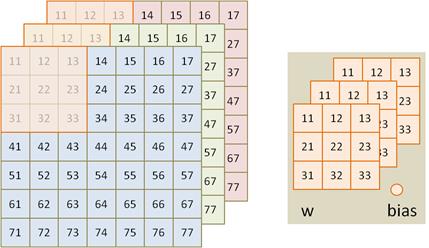
Математики обобщили эту структуру и предложили следующее решение. Входной сигнал изображения пропускается через фильтр небольшого размера, например, 3х3 с весами:
Этот фильтр последовательно скользит по двумерному сигналу (изображению) с заданным шагом, допустим, 1 пиксель, и формирует выходные значения по формуле:
Здесь
Сканируя весь двумерный тензор (изображение), на выходе получается двумерная матрица выходных значений для текущего фильтра. Эту матрицу принято называть картой признаков, а сам фильтр – ядром. Однако на этом работа сверточного слоя не заканчивается. Весь процесс повторяется, но уже с другим ядром того же размера. Получается еще одна карта признаков. И так для всего заданного количества ядер. В результате на выходе получаем множество карт признаков одинакового размера, которые представляют собой набор каналов. Это и есть общий результат работы сверточного слоя.
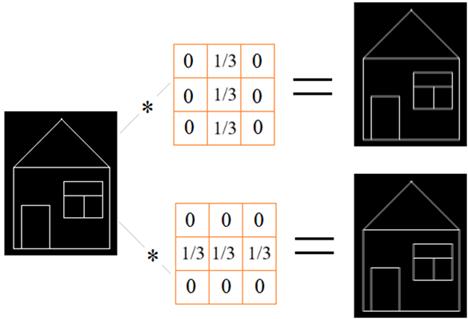
Конечно, здесь вполне может возникнуть вопрос, в чем смысл такого преобразования входного сигнала? Что особенного нам это дает? Давайте представим, что у нас имеется схематичное изображение дома и мы пропускаем его через следующие ядра (фильтры):
На выходе получаем отчетливые вертикальные линии в первом случае и горизонтальные – во втором. Все остальные линии стали более бледными. То есть, фильтр позволяет выделять характерные участки на изображении в соответствии с конфигурацией весовых коэффициентов. То есть, когда на изображении появляется характерный фрагмент, подходящий под ядро фильтра, то на его выходе формируется значимый отклик. Причем местоположение характерного фрагмента на изображении не имеет значения, т.к. каждый фильтр сканирует все пространство входного сигнала и рано или поздно он будет обработан. В этом одно из преимуществ сверточных НС – они инвариантны (независимы) от местоположения объектов на изображении.
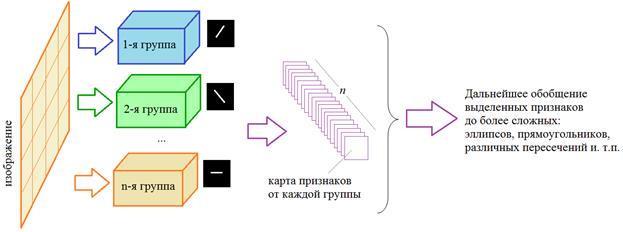
Значимые величины в каждой карте показывают наличие признака в строго определенном месте изображения. Группы таких признаков будут обобщаться на последующих сверточных слоях, выделяя все более сложные особенности, например, круги, эллипсы, прямоугольники, различные пересечения и т.п.
Вот пример карт признаков на разных сверточных слоях НС, обученной классификации изображений лиц людей:
Как видим, каждый последующий слой обобщает и выделяет более крупные признаки. На последнем слое уже просматриваются различные шаблоны лиц людей целиком. До сих пор мы с вами рассматривали простейший вариант, когда на вход подавалось одноканальное изображение, например, в градациях серого. Если же обрабатывается полноцветное изображение, представленное, например, тремя цветовыми компонентами RGB, то применяется трехмерный фильтр для формирования карты признаков:
То есть, каждое выходное значение карты для текущего ядра вычисляется согласно выражению:
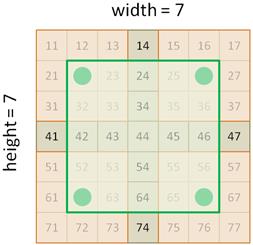
В результате все три канала входного изображения объединяются посредством фильтра и на выходе по-прежнему получаем двумерную карту признаков. Следующий важный момент, на который вы возможно уже обратили внимание, это уменьшение размера карты признаков по сравнению с размером входного сигнала. Например, если изображение имеет размеры 7x7 элементов, а ядра 3x3 элемента, то размер формируемой карты признаков получается 5x5:
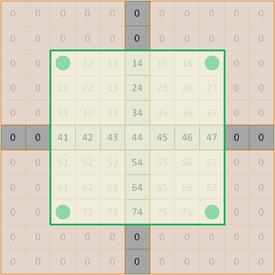
И это не всегда желаемый результат. Не редко требуется, чтобы размеры карт признаков совпадали с размером входного сигнала (по числу строк и столбцов, без учета числа каналов). В этом случае применяют довольно распространенный прием из обработки изображений: расширяют размер входного сигнала, заполняя новые элементы, как правило, нулями. Если добавить по одному набору таких элементов с каждой стороны:
то ядра размером 3x3, двигаясь с шагом 1, на выходе сформируют карту признаков размером 7x7. Если бы ядра имели другой размер, например, 5x5, то следовало бы добавить по два набора нулевых элементов с каждой стороны:
То есть, конфигурация нулевой зоны зависит от размеров фильтров и желаемого конечного результата. Pooling (изменение масштаба)Так, в целом, выглядит работа сверточного слоя, на выходе которого формируется набор из карт признаков. Что делается дальше? А дальше предполагается анализировать вычисленные признаки на более крупном масштабе. Для этого размерность карт признаков сокращают с помощью одной из операций:
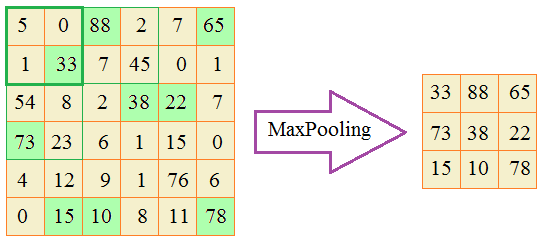
Чаще всего используют MaxPooling, которая работает следующим образом. Вся карта признаков покрывается непересекающимися блоками, например, размером 2x2 элемента. И в пределах каждого блока отбирается наибольшее значение. Эти величины и составляют результат работы операции MaxPooling.
Например, вот так отработала операция MaxPooling с пикселями реального изображения, уменьшая его размер в два раза:
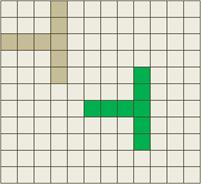
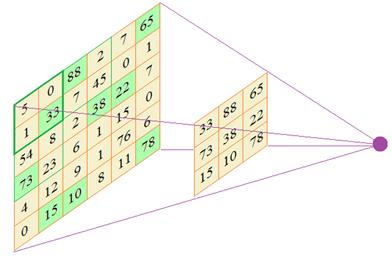
Как видим, информация в целом сохранилась даже на последнем этапе, где по-прежнему просматривается знак пешеходного перехода. Но, все же, какую роль играет эта операция в сверточных НС? Как мы говорили, наша цель выполнять анализ вычисленных признаков на все более и более крупном масштабе. Именно это дает нам операция Pooling. Смотрите, если на следующем сверточном слое анализировать выделенные максимальные значения ядрами с теми же размерами 3х3, то это эквивалентно обработке максимальных значений карты признаков, но уже в области размером 6х6:
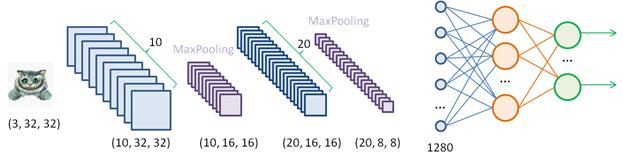
В результате получаем анализ данных на более крупном масштабе и благодаря этому, нейроны следующего слоя способны выделять более общие признаки на изображении. Итоговая архитектураДавайте подытожим изложенный материал и посмотрим на общую архитектуру сверточных НС. Для простоты положим, что на вход подается изображение размером 32 x 32 пиксела и оно проходит через 10 ядер первого скрытого слоя:
На выходе получаем набор значений в виде тензора размерностью 10x32х32 элементов. Далее, применяется операция MaxPooling для перехода на более крупный масштаб. Следующий слой имеет уже 20 различных фильтров. На выходе получаем тензор размерностью 20x16х16. Операция MaxPooling сокращает размерность тензора до 20x8х8. Такие преобразования можно продолжать и далее, пока карты признаков не станут размером 1x1 пиксел. Или же можно остановиться на любом этапе преобразования и подать полученный тензор на вход обычной полносвязной сети. Конечный этап сверточной НС в задачах классификации или регрессии, обычно завершается полносвязной сетью, на выходе которой получаем итоговый выходной сигнал. Курс по нейронным сетям: https://stepik.org/a/227582 Видео по теме |