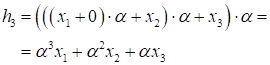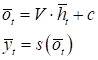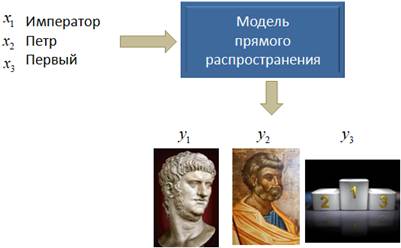
|
Введение в рекуррентные нейронные сетиДо сих пор мы с вами рассматривали сети прямого распространения, когда входной сигнал последовательно, слой за слоем проходит по всей сети и на выходе формируется некоторый ответ. Недостатком таких сетей является сложность анализа временных последовательностей, например, звукового сигнала, изменение положения объекта во время движения, текстовая информация и многое другое. Во всех этих примерах важно «знание» предыдущих элементов последовательности при их анализе. Например, если на вход НС подавать отдельные слова фразы: «Император Петр Первый» то на выходе она, скорее всего, будут формироваться несвязанные прогнозы, не отражающие суть этой фразы целиком:
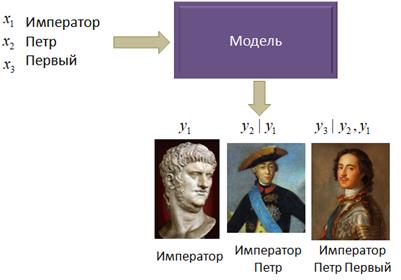
Но, если бы сеть
могла улавливать взаимосвязи между отдельными элементами входных данных
Конечно, первое, что приходит в голову, это подавать на вход сети не отдельные слова, а фразы целиком, и ожидать, что модель в этом случае обучится правильно воспринимать произвольные текстовые данные, на которые была обучена.
Но здесь сразу
возникает две сложности. Во-первых, размер фраз может быть разным и нужно
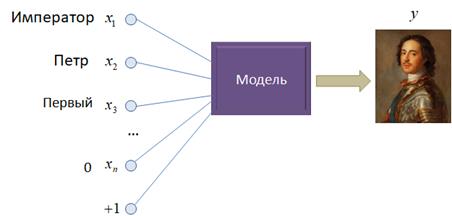
придумать, как выравнивать эти данные при подаче их на входы Как же организовать обработку таких данных, к которым, я напомню, относится не только текст, но и любые взаимосвязанные между собой последовательности, такие как звук, видео, траектории движения и т.п? Так как длина последовательностей может быть произвольной, то было бы хорошо ее подавать поэлементно на вход нейронной сети для формирования одного или нескольких выходных значений:
Такой подход, в частности, поможет описать модель без привязки к размерам входных данных, а также справиться с проблемой порядка слов в похожих фразах (последовательностях). Осталось понять, как учесть при этом взаимосвязи между элементами последовательности в самой модели? Один из таких способов известен со стародавних времен. Давайте каждое входное значение обрабатывать некоторой функцией:
И пусть для наглядности она будет следующей:
где
Отсюда хорошо
видно, что величина Рекуррентный слойКонечно, это
примитивный пример, который лишь показывает принцип, возможности целостной
обработки поступающей информации в виде последовательного набора отдельных
элементов
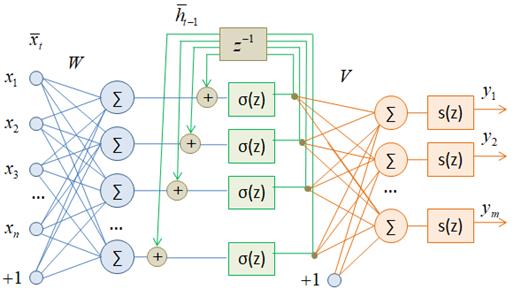
Здесь входной
сигнал
Затем, вектор
Далее этот вектор подается снова на вход этого же слоя и на выходной слой нейронов с матрицей V, где формируются значения:
Благодаря
наличию рекуррентного слоя выходное значение Здесь вы можете
спросить: а откуда брать значение
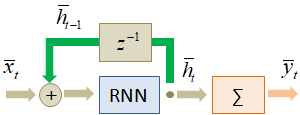
Это общепринятые начальные условия работы рекуррентных сетей. Исторически первой сетью такого типа была сеть Хопфилда, окончательно оформленная в 1982 г. Она используется в своем, узком классе задач. А первой современной рекуррентной моделью стала сеть Джеффа Элмана, представленная в 1990 г. На ее основе создаются простейшие рекуррентные сети по описанной архитектуре. По-английски рекуррентная нейронная сеть записывается как Recurrent Neural Network (RNN). Сокращение RNN мы в дальнейшем будем использовать для обозначения рекуррентных слоев. Способы изображений и виды рекуррентных слоевКонечно, в таком развернутом виде каждый раз изображать рекуррентные слои нейронных сетей не очень удобно. Поэтому часто в литературе можно встретить более компактные и простые представления, например, такое:
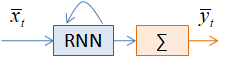
Или такое:
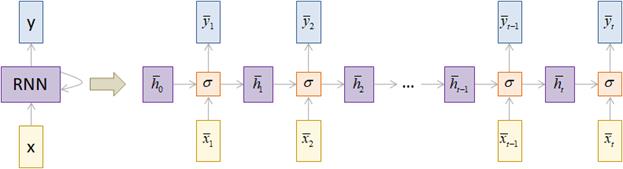
В дальнейшем мы также будем использовать такие упрощения в изображениях архитектур рекуррентных нейронных сетей. Довольно популярной практикой является представление рекуррентных сетей в виде ее развертки во времени.
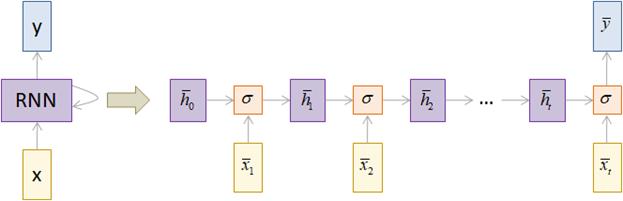
Здесь сеть как бы развернута во времени и мы наглядно видим каждый шаг ее работы. Такая архитектура, когда множеству входных векторов соответствует множество выходных, называется Many-to-Many. По аналогии, можно строить архитектуры Many-to-One:
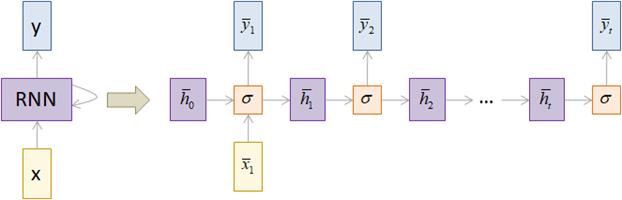
и One-to-Many:
Какую архитектуру, когда выбирать подсказывает сама прикладная задача. Например, при переводе с одного языка на другой имеем произвольную последовательность слов и на выходе также получаем последовательности произвольной длины, значит, здесь следует использовать аналог архитектуры Many-to-Many. Вот несколько примеров:
Обучение рекуррентных нейронных сетейИз разверток рекуррентного слоя во времени хорошо видно, что рекуррентные сети можно обучать известным нам алгоритмом Back Propagation, так как здесь имеем аналог многослойной сети. Но есть и несколько нюансов. Во-первых, на вход каждого нейрона поступает не только входной сигнал, но и предыдущее состояние сети. Эти вычисления нужно делать строго последовательно, поэтому распараллелить процесс рекуррентных вычислений невозможно, либо крайне сложно. В результате время обучения рекуррентных сетей, как правило, выше, аналогичных сетей прямого распространения. Во-вторых, весовые коэффициенты едины для всех слоев развернутой сети, так как это, фактически, один и тот же слой, только на разных итерациях вычисления. Это также следует учитывать при разработке алгоритма обучения. Но все это незначительно меняет исходную идею градиентного спуска для корректировки весовых коэффициентов и такой модифицированный алгоритм применительно к рекуррентным нейронным сетям существует и называется: Back-propagation Through Time (BPTT) Здесь понятие Through Time (сквозь время) как раз относится к учету предыдущих вычислительных шагов, развернутых во времени, при вычислении локальных градиентов. Так как все предыдущие состояния влияют на выходные значения сети, а значит, и на заданный критерий качества. На этом мы завершим начальный обзор рекуррентных НС. Конечно, мы здесь сделали только первый шаг в понимании их работы и не затронули некоторые другие важные архитектуры, например, LSTM и GRU. Но, обо всем по порядку. Сначала нужно разобраться с работой базовых RNN-сетей, а затем, переходить к более сложным аналогам. Видео по теме |
,
то шансы правильно оценить смысл этой фразы у нее бы сильно вырос:
.
Да и само значение n тоже нужно правильно подобрать. Вторая значимая
проблема состоит в возможности изменения порядка следования слов одной и той же
фразы. Например, вместо «Император Петр Первый» вполне возможен вариант «Петр
Первый Император». А потом еще и добавлено «Всероссийский». Но, несмотря на
изменение порядка и размера, смысл фразы остается прежним.
-
некоторый коэффициент. Тогда для первых трех входных элементов значение 
можно
записать в следующем развернутом виде:
.
Все, что нам остается, – это заложить в архитектуру нейронной сети тот же самый
подход, реализующий функцию вида 
с
нейронов текущего слоя снова подать на вход этого же слоя с задержкой на один
такт. В результате приходим к идее построения рекуррентных слоев нейронной
сети:
умножается
вначале на матрицу весовых коэффициентов W и результат
суммируется с предыдущим выходным значением 
:
пропускается
через функцию активации 
и
формируется значение вектора 
:
строится
с учетом всех поступивших на момент времени t входных
значений 
.
,
когда на вход подается самый первый вектор 
?
У нас же еще нет предыдущего состояния сети? Все верно, и логично будет взять
этот начальный вектор нулевым:
