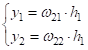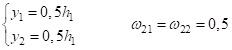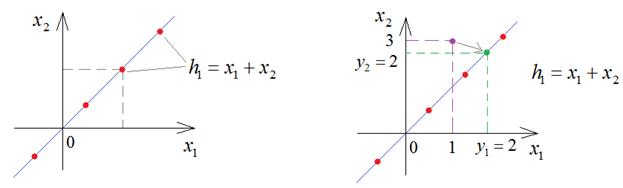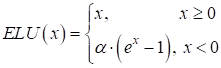|
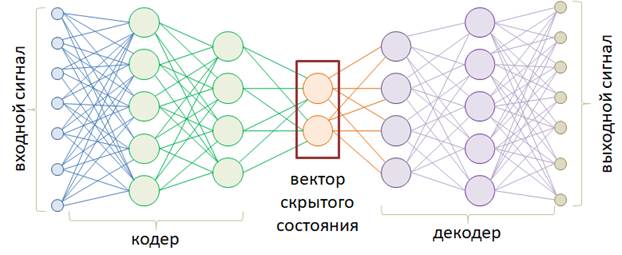
Введение в автоэнкодерыКурс по нейронным сетям: https://stepik.org/a/227582 Теперь, когда мы с вами в целом разобрались с основными архитектурами НС и примерами их использования, поговорим о некоторых распространенных, интересных и полезных их построениях, в частности, об автоэнкодерах. В самом простом варианте автоэнкодер – это НС, которая сначала кодирует входной сигнал в некоторое скрытое состояние, размерность которого, как правило, меньше размерности входного сигнала, а затем, из скрытого состояния снова разворачивает (декодирует) данные в другое, новое состояние:
Размерности входных и выходных векторов, в общем случае, могут отличаться. Например, можно попробовать обучить автоэнкодер масштабировать изображения. В другом примере сжатия данных, декодер должен как можно точнее воспроизвести входное изображение, опираясь только на вектор скрытого состояния. Сам же этот вектор будет представлять сжатое изображение. Правда, НС в области сжатия работают хуже традиционных алгоритмов, поэтому автоэнкодеры нашли свое применение в других областях. Например, сеть U-Net, которую мы с вами реализовывали для задачи семантической сегментации объектов на изображении, по сути, является автоэнкодером, преобразуя сначала исходное изображение в компактное представление, а затем, декодируя его, формируя результат сегментации. Другой распространенный пример автоэнкодера – это архитектура seq2seq, состоящая из двух рекуррентных сетей: одна играет роль кодера, а вторая – декодера. В частности так можно реализовать простейший переводчик с одного языка на другой. В целом, автоэнкодеры охватывают большой пласт различных задач, где требуется сначала закодировать входной сигнал, а затем, выполнить его декодирование в требуемом формате. Давайте вначале в целом разберемся в принципах работы автоэнкодеров. Для этого возьмем простейшую модель с линейной функцией активации следующего вида:
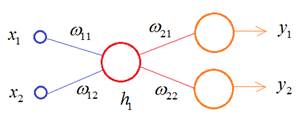
В этой схеме кодер выполняет очень простую операцию:
А декодер
разворачивает значение
Предположим, что
значение
Затем, декодер пытается восстановить снова эти два значения и делает это, допустим, следующим образом:
В результате,
получаем модель представления входных данных в скрытом состоянии
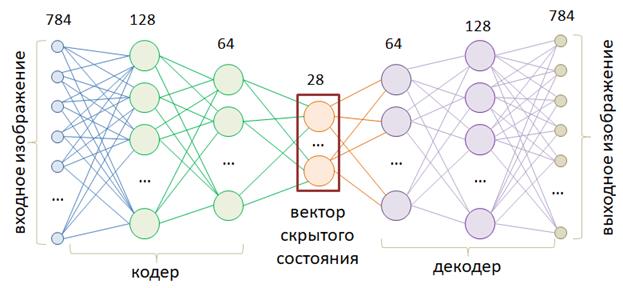
Пока входные данные соответствуют этой модели, т.е. лежат на этой линии, декодер их точно восстанавливает. Как только их положение меняется, например, 3 и 1, то кодер дает сумму 4 и декодер интерпретирует это значение как 2 и 2. Вот этот момент здесь ключевой: вектор скрытого состояния описывает некую модель представления данных. И чем точнее эта модель описывает входные значения, тем лучше декодер сможет их восстанавливать. Конечно, НС с линейной функцией активации может формировать модель только в виде линии (одномерный случай) или гиперплоскости (многомерный случай). Но, используя нелинейные активационные функции (сигмоида, ReLU и т.п.) можно формировать практически любую модель. И эта модель создается в процессе обучения автоэнкодера. Давайте реализуем относительно простой автоэнкодер в виде многосвязной НС для представления изображений цифр из БД MNIST, с которой ранее мы уже работали. На этом примере мы наглядно увидим результат использования сложной нелинейной модели. Вначале опишем модель автоэнкодера следующим образом: class AutoEncoderMNIST(nn.Module): def __init__(self, input_dim, output_dim, hidden_dim): super().__init__() self.hidden_dim = hidden_dim self.encoder = nn.Sequential( nn.Linear(input_dim, 128), nn.ELU(inplace=True), nn.Linear(128, 64), nn.ELU(inplace=True), nn.Linear(64, self.hidden_dim) ) self.decoder = nn.Sequential( nn.Linear(self.hidden_dim, 64), nn.ELU(inplace=True), nn.Linear(64, 128), nn.ELU(inplace=True), nn.Linear(128, output_dim), nn.Sigmoid() ) def forward(self, x): h = self.encoder(x) x = self.decoder(h) return x, h Здесь класс nn.ELU описывает функцию активации ELU(x) вида:
А сама модель соответствует следующей структуре полносвязной нейронной сети:
На выходе автоэнкодер будет формировать сигнал размерностью 28*28=784 элемента со значениями в диапазоне [0; 1]. Входной сигнал так же представлен в диапазоне чисел [0; 1]. Размер вектора скрытого состояния равен 28. То есть, весь входной сигнал в 784 элемента будет кодироваться в вектор 28 элементов. Затем, декодер должен будет по этому вектору восстановить исходный сигнал. После этого создадим модель и сформируем обучающую выборку: model = AutoEncoderMNIST(28 * 28, 28 * 28, 28) transforms = tfs_v2.Compose([tfs_v2.ToImage(), tfs_v2.ToDtype(dtype=torch.float32, scale=True), tfs_v2.Lambda(lambda _img: _img.ravel())]) d_train = torchvision.datasets.MNIST(r'C:\datasets\mnist', download=True, train=True, transform=transforms) train_data = data.DataLoader(d_train, batch_size=32, shuffle=True) Зададим оптимизатор, функцию потерь, в виде средней квадратической ошибки, пять эпох обучения, и переведем модель в режим обучения: optimizer = optim.Adam(params=model.parameters(), lr=0.001) loss_func = nn.MSELoss() epochs = 5 model.train() Запишем главный цикл обучения знакомым нам образом: for _e in range(epochs): loss_mean = 0 lm_count = 0 train_tqdm = tqdm(train_data, leave=True) for x_train, y_train in train_tqdm: predict, _ = model(x_train) loss = loss_func(predict, x_train) optimizer.zero_grad() loss.backward() optimizer.step() lm_count += 1 loss_mean = 1/lm_count * loss.item() + (1 - 1/lm_count) * loss_mean train_tqdm.set_description(f"Epoch [{_e+1}/{epochs}], loss_mean={loss_mean:.3f}") Сохраним обученную модель: st = model.state_dict() torch.save(st, 'model_autoencoder.tar') и отобразим первые 10 изображений с результатом их декодирования обученным автоэнкодером: n = 10 model.eval() plt.figure(figsize=(2*n, 2*2)) for i in range(n): img, _ = d_train[i] predict, _ = model(img.unsqueeze(0)) predict = predict.squeeze(0).view(28, 28) img = img.view(28, 28) dec_img = predict.detach().numpy() img = img.detach().numpy() ax = plt.subplot(2, n, i+1) plt.imshow(img, cmap='gray') ax.get_xaxis().set_visible(False) ax.get_yaxis().set_visible(False) ax2 = plt.subplot(2, n, i+n+1) plt.imshow(dec_img, cmap='gray') ax2.get_xaxis().set_visible(False) ax2.get_yaxis().set_visible(False) plt.show() После запуска программы получим следующие изображении:
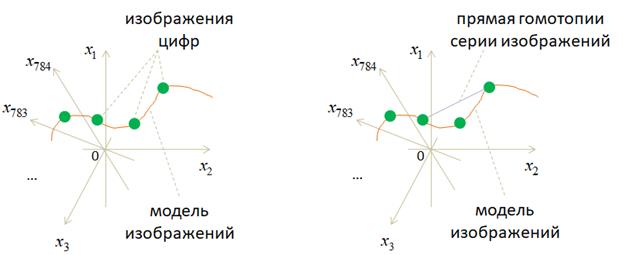
Как видите, результаты получились вполне сносными, с небольшими отличиями, так как вектор скрытого состояния способен удерживать лишь значимые детали входных изображений. Мелкие детали получаются расплывчатыми, смазанными. Как можно объяснить возможность сжатия входного сигнала до вектора в 28 отсчетов? Смотрите, любое изображение размером 28х28 пикселей можно представить как точку в 784-мерном пространстве. Большинство точек этого пространства будут соответствовать шумовым, непонятным изображениям и только малая их часть соответствует цифрам. Кодер в процессе обучения пытается «уловить» область определения этих цифр в многомерном пространстве и представить их в 28-мерном пространстве вектора скрытого состояния:
Давайте отобразим цифры, которые получаются гомотопией между двумя изображениями пятерок по прямой. Выполним это с помощью следующего фрагмента программы: st = torch.load('model_autoencoder.tar', weights_only=True) model.load_state_dict(st) n = 10 model.eval() plt.figure(figsize=(2*n, 2*2)) # фрагмент для формирования и отображения гомотопии изображений по прямой frm, to = d_train.data[d_train.targets == 5][10:12] frm = transforms(frm) to = transforms(to) for i, t in enumerate(np.linspace(0., 1., n)): img = frm * (1-t) + to * t # Гомотопия по прямой predict, _ = model(img.unsqueeze(0)) predict = predict.squeeze(0).view(28, 28) dec_img = predict.detach().numpy() img = img.view(28, 28).numpy() ax = plt.subplot(2, n, i+1) plt.imshow(img, cmap='gray') ax.get_xaxis().set_visible(False) ax.get_yaxis().set_visible(False) ax2 = plt.subplot(2, n, i+n+1) plt.imshow(dec_img, cmap='gray') ax2.get_xaxis().set_visible(False) ax2.get_yaxis().set_visible(False) plt.show() Получим следующий результат:
Смотрите, простое движение по прямой между двумя образами дает нам проявление второй пятерки и плавное затемнение первой. Но когда мы преобразуем эти промежуточные изображения в вектор скрытого состояния (с помощью кодера), то переходим в область найденной модели и затем, декодер, восстанавливает текущий скрытый вектор до полного изображения. В результате, мы двигаемся уже по точкам внутри сформированной модели, и серия изображений выглядит уже более естественной. Фактически, здесь мы сгенерировали серию изображений превращения первой пятерки во вторую. Изображения получились не очень хорошие, особенно в средней области. Результат можно постараться улучшить, используя сверточные НС и увеличив размерность вектора скрытого состояния. Но далее мы пойдем другим путем и рассмотрим довольно популярную технику компактного представления входных данных в векторе скрытого состояния с помощью вариационного автоэнкодера. Курс по нейронным сетям: https://stepik.org/a/227582 Видео по теме |