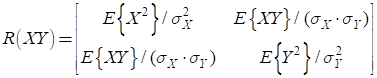|
Тензоры. Тригонометрические и статистические функцииНа этом занятии рассмотрим основные математические функции при работе с тензорами пакета PyTorch. Методы sum, mean, min и maxИтак, очень часто на практике требуется вычислять сумму значений элементов тензоров, их среднее значение, а также находить минимальные и максимальные значения. Для этих целей в PyTorch существуют встроенные методы тензоров, выполняющие эти действия, и сейчас мы посмотрим, как они работают. Пусть имеется одномерный тензор: a = torch.FloatTensor([ 1, 2, 3, 10, 20, 30]) Вычислим сумму, среднее значение и найдем максимальное и минимальное значения: a.sum() # tensor(66.) a.mean() # tensor(11.) a.max() # tensor(30.) a.min() # tensor(1.) Как видите, все достаточно просто. Аналогичным образом все эти методы работают и с многомерными массивами: a = a.view(3, 2) # тензор формы 3x2 a.sum() # tensor(66.) Но, если требуется вычислить сумму только по какой-то одной оси, то ее можно явно указать дополнительным параметром: a.sum(dim=0) # array([24, 42]) a.sum(dim=1) # array([ 3, 13, 50]) a.mean(dim=0) # tensor([ 8., 14.]) Похожим образом работают и остальные два метода: a.max(dim=1) получим: torch.return_types.max(values=tensor([ 2., 10., 30.]), indices=tensor([1, 1, 1])) То есть, здесь возвращается последовательность из двух элементов. Чтобы выделить только максимальные значения нужно дополнительно указать атрибут values: a.max(dim=1).values # tensor([ 2., 10., 30.]) Либо воспользоваться аналогичными методами, предназначенными для многомерных тензоров: a.amax(dim=1) # tensor([ 2., 10., 30.]) a.amin(dim=0) # tensor([1., 2.]) Базовые математические функцииВсе те же самые операции и многие другие можно выполнять через функции пакета PyTorch, а не через методы тензоров. Вот список основных из них:
Предположим, имеется тензор: a = torch.IntTensor([-1, 1, 5, -44, 32, 2]) Тогда для вычисления модулей значений его элементов можно записать команду: torch.abs(a) # array([ 1, 1, 5, 44, 32, 2]) На выходе получаем новый массив с абсолютными величинами. Или, если необходимо изменить значения текущего тензора, то можно вызвать метод: a.abs_() # tensor([ 1, 1, 5, 44, 32, 2]) Остальные функции работают по аналогии, например: torch.amax(a) # tensor(32) torch.log(a) # tensor([ nan, 0.0000, 1.6094, nan, 3.4657, 0.6931]) torch.round(a) # tensor([ -1, 1, 5, -44, 32, 2]) Функции, применяемые поэлементно к тензору, как правило, имеют inplace аналоги. Например: a = a.float() a.log_() a = torch.FloatTensor([-1, 1, 5, -44, 32, 2]) a.round_() И так со всеми остальными функциями и методами. Тригонометрические функции и методыСледующий набор часто используемых методов (и функций) связаны с различными тригонометрическими функциями. Наиболее употребительные из них приведены в следующей таблице:
Пусть для примера объявлен следующий тензор: a = torch.linspace(0, torch.pi, 10) С ним возможны следующие команды: r = np.sin(a) # возвращает тензор синусов углов для каждого значения a.cos() # возвращает тензор косинусов углов a.tan_() # изменяет текущий тензор на тангенсы углов И так со всеми тригонометрическими методами и функциями. Функции математической статистикиПоследняя группа общематематических функций, которую мы рассмотрим на этом занятии, отвечает за вычисления статистических характеристик случайных величин. Основные из них, следующие:
Рассмотрим работу этих функций. Предположим, имеются следующие тензоры: x = torch.FloatTensor([1, 4, 3, 7, 10, 8, 14, 21, 20, 23]) y = torch.FloatTensor([4, 1, 6, 9, 13, 11, 16, 19, 15, 22]) Эти числа будем воспринимать как реализации случайных величин X и Y. Тогда, для вычисления медианы СВ X, можно воспользоваться функцией: torch.median(x) # tensor(8.) Для расчета дисперсии и СКО, например, методами: x.var() # tensor(63.6556) y.std() # tensor(6.7032) Далее, чтобы рассчитать коэффициент корреляции Пирсона, объединим массивы x и y в единый тензор: XY = torch.vstack([x, y]) # каждый тензор в отдельной строке Тензор XY примет вид: tensor([[
1., 4., 3., 7., 10., 8., 14., 21., 20., 23.],
И выполним функцию: torch.corrcoef(XY) Результатом будет тензор 2x2: tensor([[1.0000, 0.9316],
Как ее следует интерпретировать? В действительности, это автокорреляционная матрица вектора СВ [X, Y]:
(В этой формуле полагается, что СВX и Y центрированы, то есть имеют нулевое математическое ожидание). Если нужно вычислить не нормированное МО, то есть, автоковариационную матрицу, то следует воспользоваться функцией: torch.cov(XY) # ковариационная матрица размерностью 2x2 Получим: tensor([[63.6556,
49.8222],
Конечно, мы рассмотрели далеко не все математические функции тензоров PyTorch. На следующем занятии продолжим эту тему и поговорим об умножении векторов, матриц и линейной алгебре. Видео по теме |
