|
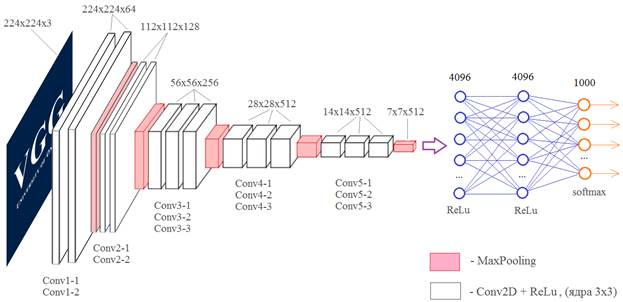
Сверточные нейронные сети VGG-16 и VGG-19Курс по нейронным сетям: https://stepik.org/a/227582 На этом занятии рассмотрим две довольно популярные архитектуры СНС от компании Visual Geometry Group: VGG-16 и VGG-19 разработанные для распознавания объектов на изображениях. В 2014-м году сеть VGG-16 на соревнованиях по распознаванию изображений базы ImageNet достигла небывалой на тот момент точности в 92,7%. И по этому показателю почти сравнялась с человеком. Теперь она выложена в открытом доступе (причем, с обученными весовыми коэффициентами), чтобы каждый желающий мог проводить с ней любые эксперименты. Итак, общая структура сети VGG-16, следующая:
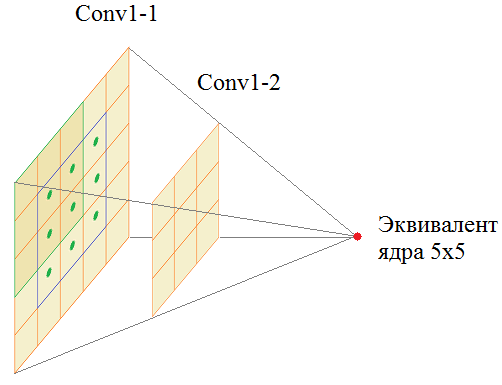
На вход подается полноцветное изображение с тремя каналами RGB. Затем, оно последовательно проходит через сверточные слои Conv1-1 и Conv1-2, каждый имеет по 64 фильтра с размером ядер 3х3. Далее, операция MaxPooling уменьшает вдвое линейные размеры карт признаков и результат обрабатывается двумя последовательными слоями Conv2-1 и Conv2-2 со 128 фильтрами с тем же размером ядер 3х3. И так далее. Потом через три сверточных слоя все проходит, потом еще через три. Результирующий тензор размером 7х7х512 подается на полносвязную НС с 4096 нейронами двух скрытых слоев и 1000 нейронами выходного слоя. Число 1000 соответствует количеству классов, на которые эта сеть была обучена. У вас может возникнуть вопрос: а зачем здесь ставится два подряд, а то и три сверточных слоя? Почему нельзя обойтись одним? На самом деле можно. Вместо первых двух слоев Conv1-1 и Conv1-2 с ядрами 3х3 пикселя можно использовать один эквивалентный слой с ядрами 5х5 пикселей:
Хорошо, но тогда почему бы один такой слой и не использовать вместо двух? Дело в том, что число параметров у ядра 5х5 равно: 5 * 5 + 1 = 26 (здесь +1 – это bias). А у двух ядер 3х3: 2 * (3 * 3 + 1) = 20 То есть, два подряд идущих сверточных слоя имеют меньше настраиваемых параметров, чем один с ядром 5х5. И, во-вторых, вычисления на графических процессорах оптимизированы для матриц 3x3. Вот основные причины использования в архитектуре сети VGG-16 двух подряд слоев с ядрами 3x3 вместо одного с ядром 5x5. Я думаю, вам теперь понятна вся структура этой сети. В краткой записи она выглядит так:
Во втором столбце представлена аналогичная архитектура сети VGG-19. Как вы уже догадались, здесь числа 16 и 19 означают общее количество слоев в нейронной сети. Преимуществом этих сетей является их относительная простота. А недостатком – медленная скорость обучения и большое количество весовых коэффициентов. Если их все сохранить на диск, то получится объем примерно 528 Мб. Реализация VGG-сетей в PyTorchФреймворк PyTorch позволяет использовать уже обученные НС VGG16, VGG19 и некоторые другие для своих целей. Подробную информацию о них можно посмотреть на странице официальной документации: https://pytorch.org/vision/master/models/vgg.html Вначале нужно импортировать модуль torchvision.models, например, так: from torchvision import models и создать модель с помощью соответствующего класса:
Например, чтобы сформировать модель VGG-16 в самом простом варианте можно записать: model = models.vgg16() При просмотре этой модели увидим вначале наборы сверточных слоев, а в конце полносвязные слои. Обратите внимание, что эта модель использует метод Dropout для борьбы с переобучением. Однако такая модель состоит из случайных весовых коэффициентов, то есть, не обучена. Чтобы загрузить и использовать обученный вариант, необходимо дополнительно прописать параметр weights одним из следующих способов: model = models.vgg16(weights=models.VGG16_Weights.DEFAULT) model = models.vgg16(weights=models.VGG16_Weights.IMAGENET1K_V1) model = models.vgg16(weights='DEFAULT') model = models.vgg16(weights='IMAGENET1K_V1') Все эти команды будут давать один и тот же результат. Поэтому применяется тот, что удобнее. Я оставлю вариант: model = models.vgg16(weights='DEFAULT') Кроме того, можно отдельно воспользоваться объектом: vgg_weights = models.VGG16_Weights.IMAGENET1K_V1 или vgg_weights = models.VGG16_Weights.DEFAULT который, затем, можно указывать в параметре weights: model = models.vgg16(weights=vgg_weights) Что нам это дает? Смотрите, объект vgg_weights содержит довольно полезную информацию о классах в словаре: cats = vgg_weights.meta['categories'] и применяемые трансформации к входному сигналу: transforms_1 = vgg_weights.transforms() Все это потом можно использовать в своей программе. И мы, как раз, это сейчас сделаем. Давайте возьмем некоторое изображение, например, спортивного автомобиля:
И пропустим через обученную сеть VGG16. Для этого загрузим изображение: img = Image.open('img_2.jpg').convert('RGB') Применим к нему трансформации сети VGG16: img_net = transforms_1(img).unsqueeze(0) Напомню, что метод unsqueeze(0) добавляет первую ось, чтобы получить тензор формата: (1, 3, 224, 224) Здесь первая размерность – это число наблюдений в пакете (batch), в данном случае одно изображение. Пропускаем тензор img_net через сеть VGG16: model.eval() p = model(img_net).squeeze() # (1000) Обратите внимание на обязательный вызов метода eval, который переводит модель в режим эксплуатации. Если этого не сделать, то слои Dropout сети VGG16 будут работать в режиме обучения и из-за этого сеть будет формировать не совсем корректные результаты. А метод squeeze удаляет первую ось, которую мы добавляли ранее методом unsqueeze. В итоге тензор p будет содержать выходные значения НС. Так как последний слой в модели не имеет функции активации, то для интерпретации значений вектора p в терминах вероятности пропустим его значения через функцию активации softmax с последующим упорядочиванием результатов по убыванию значений: res = p.softmax(dim=0).sort(descending=True) Выведем пять наиболее вероятных значений следующим образом: for s, i in zip(res[0][:5], res[1][:5]): print(f"{cats[i]}: {s:.4f}") После выполнения программы получим результат: sports car:
0.9474
Как видите, сеть VGG16 достаточно уверенно классифицировала спортивный автомобиль на изображении. И в заключение еще несколько важных замечаний. В ряде практических задач в сетях VGG достаточно использовать только сверточные слои без полносвязных. Для этого модель model содержит два атрибута:
Например, команда: mf = model.features выделит последовательную модель mf, состоящую только из сверточных слоев. То есть, ей так же можно подать на вход подготовленное изображение img_net: res = mf(img_net) И мы в последующем воспользуемся этим функционалом. Вот так применяется сеть VGG16. По аналогии используются все остальные VGG-модели. Курс по нейронным сетям: https://stepik.org/a/227582 Видео по теме | ||||||||||||||||||||||||||||||||||||||||||||||||||