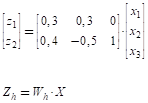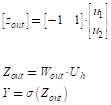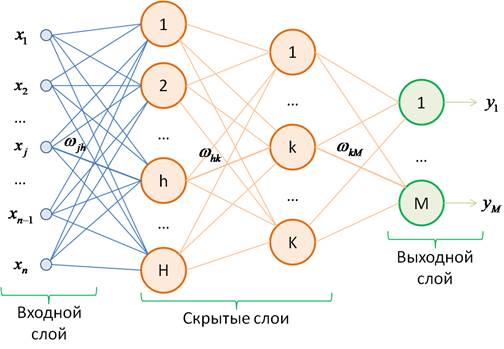
|
Структура и принцип работы полносвязных нейронных сетейКак я отмечал во введении, простейшая НС – персептрон, представляет собой довольно упрощенную попытку имитации работы биологической сети, состоящей из нейронов, соединенных между собой дендридами и аксонами:
Это классический пример полносвязной сети прямого распространения. Здесь каждый нейрон предыдущего слоя связан с каждым нейроном следующего слоя. А сигнал распространяется от входного слоя к выходному, не образуя обратных связей. Каждая связь между нейронами имеет определенный вес:
и, сигнал, проходя по ней, меняет свое значение в соответствии с этим весом:
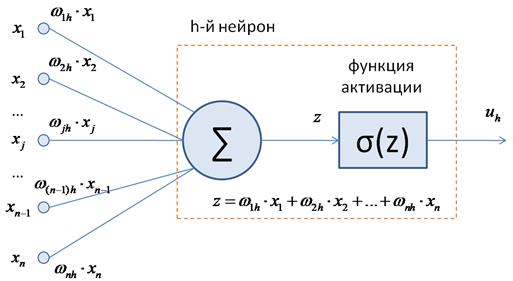
Сам по себе
нейрон – это сумматор входных сигналов, который, затем, пропускает сумму через
функцию Как я уже отмечал, в концепции персептронов функции активации выбираются пороговыми:
Например, такими:
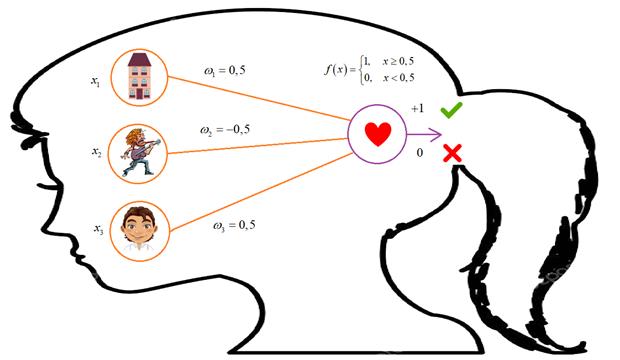
Чтобы лучше понять, как работает НС, рассмотрим очень простой и наглядный пример. Предположим, что некая девочка выбирает себе парня по трем параметрам:
Причем, везде,
«да» означает +1, а нет – 0. Наша девочка так воспитана, что положительно
относится к наличию квартиры и красоте, и отрицательно к тяжелому року. Она
больше любит лирическую музыку. Именно поэтому веса связей для дома и красивого
парня – положительные, а для рока установлено отрицательное значение. Эти веса
я прописал сам, но в общем случае они вычисляются. Об этом мы с вами еще будем
говорить. Итак, в момент знакомства, на вход ее НС поступают сигналы
Далее, это значение проходит через функцию активации:
и на выходе нейрона формируется сигнал «да» или «нет». Предположим, что ей встречается красивый парень с квартирой и обожающий тяжелый рок. Какая будет реакция? Умножаем все веса на 1, складываем, получаем сумму:
Это как раз
граничное значение порога функции Давайте теперь посмотрим на реакцию встречи с симпатичным парнем, без квартиры и равнодушного к року. Получаем сумму:
Снова на грани была сформирована симпатия. А вот если бы симпатичный парень любил рок, то было бы значение:
И шансов познакомиться с нашей девочкой у него не было бы никаких. Конечно, максимальные шансы имеет симпатичный парень с квартирой и равнодушный к року. В этом случае сумма равна:
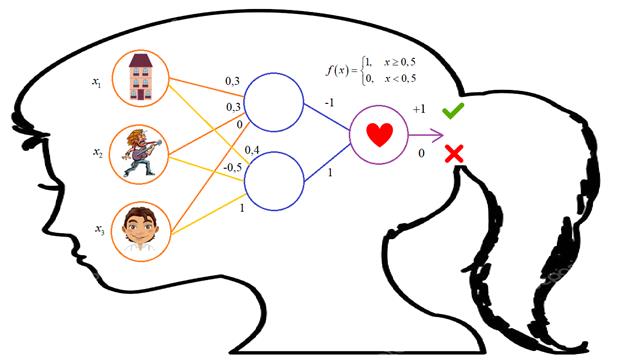
Уверенная симпатия. Вот общий принцип работы НС. Однако при такой простой структуре наша девочка не способна к сложным умозаключениям. Например, если она встречает парня с квартирой, обожающего рок, то ни за что не согласится с ним встречаться. Вне зависимости: красив он или нет. А вот если он красив, то готова пойти с ним на встречу, даже если он любит рок и не имеет квартиры. Такие более сложные выводы может позволить себе девочка с дополнительным слоем нейронов. Здесь первый нейрон скрытого слоя будет активироваться всякий раз, когда встречается парень с квартирой и обожающий рок (красота в его работе не имеет значения – вес связи равен 0). А второй нейрон этого же слоя активируется при встрече с красивым парнем. При этом остальные два фактора не имеют значения. То есть, мы здесь получаем уже некоторое обобщение наблюдаемых факторов: красивый, остальное неважно и с квартирой, но слушающий рок. Результирующая симпатия теперь будет формироваться, если первое обобщение отсутствует, а второе – присутствует. Например, встречается симпатичный молодой человек (второй нейрон загорается). Теперь важно, чтобы первый не включился. Для этого парень может любить рок, но не иметь квартиры (вероятно, она опасается, что при наличии постоянного жилья ей придется часто слышать ненавистный рок), или, иметь квартиру, но не любить рок. Или же, не иметь ни того, ни другого.
А вот если встречается по ее мнению не симпатичный парень, то второй нейрон уже не загорится и симпатия сформирована не будет, даже если у него есть квартира и он часами готов слушать лирическую музыку (значение суммы максимум будет равно 0,4 и пороговая функция выдаст 0). Для нашей девочки симпатия на первом месте! Вот так, в самом простом случае работает НС прямого распространения. Причем на уровне математики работу каждого слоя нейронов удобно записывать в векторно-матричном виде. Изначально суммирование на каждом нейроне скрытого слоя можно записать в виде:
Или, то же самое в векторно-матричном виде:
где Пропускаем суммы через функцию активации (которая, как правило, единая для всех нейронов одного слоя), получаем выходные значения нейронов скрытого слоя:
или в виде
Для вычисления значений на выходном слое имеем абсолютно те же самые математические выражения:
Как видите, работу одного слоя нейронов при прямом распространении сигнала достаточно просто и удобно представлять в виде произведения матрицы на вектор входного сигнала с последующим применением функции активации:
Причем, это общее выражение остается неизменным при любом числе входов и любом числе нейронов в текущем слое. Поэтому работу такого полносвязного слоя НС часто реализуют в виде матричных операций. Чтобы все это было понятнее, выполним реализацию рассмотренной НС с векторно-матричными вычислениями на языке Python с использованием фреймворка PyTorch. Но сделаем это после его установки и рассмотрения основных тензорных операций на следующих занятиях. Видео по теме |
-
от j-го нейрона (входа)
к h-му нейрону
,
называемую функцией активации. Выходное значение этой функции и есть
выходное значение нейрона.
в
виде значений +1 – для «да» и 0 – для «нет». Затем, каждое входное значение
умножается на вес синаптической связи, по которой следует к выходному нейрону. На
входе формируется суммарный сигнал в виде:
;
- матрица
размером 2x3 из весовых
коэффициентов; 
.
