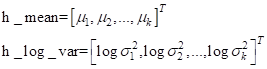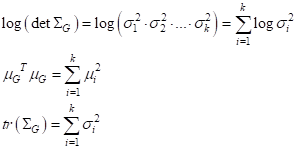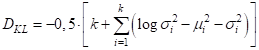|
Реализация вариационного автоэнкодера (VAE)Курс по нейронным сетям: https://stepik.org/a/227582 На предыдущем занятии мы с вами разобрали принцип построения вариационного автоэнкодера. Пришло время его реализовать с помощью PyTorch. Модель этого автоэнкодера опишем следующим образом: class AutoEncoderMNIST(nn.Module): def __init__(self, input_dim, output_dim, hidden_dim): super().__init__() self.hidden_dim = hidden_dim self.encoder = nn.Sequential( nn.Linear(input_dim, 128), nn.ELU(inplace=True), nn.BatchNorm1d(128), nn.Linear(128, 64), nn.ELU(inplace=True), nn.BatchNorm1d(64) ) self.h_mean = nn.Linear(64, self.hidden_dim) self.h_log_var = nn.Linear(64, self.hidden_dim) self.decoder = nn.Sequential( nn.Linear(self.hidden_dim, 64), nn.ELU(inplace=True), nn.BatchNorm1d(64), nn.Linear(64, 128), nn.ELU(inplace=True), nn.BatchNorm1d(128), nn.Linear(128, output_dim), nn.Sigmoid() ) def forward(self, x): enc = self.encoder(x) h_mean = self.h_mean(enc) h_log_var = self.h_log_var(enc) noise = torch.normal(mean=torch.zeros_like(h_mean), std=torch.ones_like(h_log_var)) h = noise * torch.exp(h_log_var / 2) + h_mean x = self.decoder(h) return x, h, h_mean, h_log_var Здесь появились отдельные полносвязные слои для формирования среднего значения (h_mean) и логарифма дисперсии разброса (h_log_var) для векторов скрытого состояния. А в методе forward реализована логика обработки входного тензора x и формирования выходного с дополнительным сохранением векторов скрытого состояния, их средних значений и логарифмов дисперсий. Обратите внимание, что мы работаем с логарифмом дисперсии, а не самой дисперсией. Это связано с удобством дальнейших вычислений. Поэтому в строчке: h = noise * torch.exp(h_log_var / 2) + h_mean экспонента от h_log_var / 2 соответствует СКО:
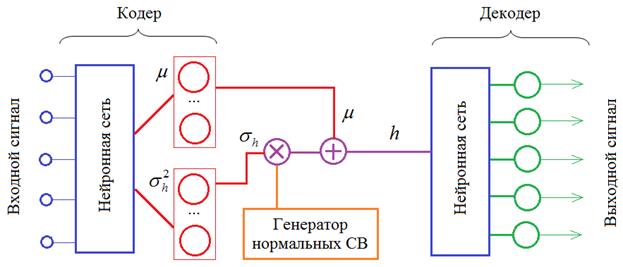
В результате модель работает согласно следующему рисунку:
Формирование функции потерьДалее нам нужно сформировать функцию потерь для обучения этой модели. Для этого объявим следующий класс: class VAELoss(nn.Module): def forward(self, x, y, h_mean, h_log_var): img_loss = torch.sum(torch.square(x - y), dim=-1) kl_loss = -0.5 * torch.sum(1 + h_log_var - torch.square(h_mean) - torch.exp(h_log_var), dim=-1) return torch.mean(img_loss + kl_loss) Мы здесь объединяем ошибку квадрата рассогласования между входным и выходным изображениями, а также дивергенцию Кульбака-Лейблера. В методе forward параметры:
Расстояние Кульбака-Лейблера вычисляется с использованием тензоров h_mean и h_log_var. Чтобы лучше понять, как работает эта строчка, положим, что величины h_mean и h_log_var – это векторы длиной k элементов:
И нам нужно получить формулу:
Распишем каждое из слагаемых (применительно к нашему случаю независимых СВ):
Значит, мы можем взять оценки векторов h_mean и h_log_var и записать все в виде: kl_loss = -0.5 * torch.sum(1 + h_log_var - torch.square(h_mean) - torch.exp(h_log_var), dim=-1) Здесь суммирование будет происходить по длине векторов h_mean и h_log_var, то есть, k раз. В итоге получится следующий вектор:
Суммируем элементы этого вектора, умножаем на -0,5, получаем расстояние Кульбака-Лейблера:
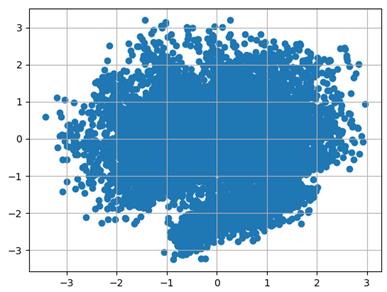
Итоговый показатель качества вычисляется, как среднее по батчам от суммы обоих величин потерь. Обучение VAEДалее, нам нужно обучить полученный вариационный автоэнкодер. Делается это стандартным образом: model = AutoEncoderMNIST(784, 784, 2) transforms = tfs_v2.Compose([tfs_v2.ToImage(), tfs_v2.ToDtype(dtype=torch.float32, scale=True), tfs_v2.Lambda(lambda _img: _img.ravel())]) d_train = torchvision.datasets.MNIST(r'C:\datasets\mnist', download=True, train=True, transform=transforms) train_data = data.DataLoader(d_train, batch_size=100, shuffle=True) optimizer = optim.Adam(params=model.parameters(), lr=0.001) loss_func = VAELoss() epochs = 5 model.train() for _e in range(epochs): loss_mean = 0 lm_count = 0 train_tqdm = tqdm(train_data, leave=True) for x_train, y_train in train_tqdm: predict, _, h_mean, h_log_var = model(x_train) loss = loss_func(predict, x_train, h_mean, h_log_var) optimizer.zero_grad() loss.backward() optimizer.step() lm_count += 1 loss_mean = 1/lm_count * loss.item() + (1 - 1/lm_count) * loss_mean train_tqdm.set_description(f"Epoch [{_e+1}/{epochs}], loss_mean={loss_mean:.3f}") st = model.state_dict() torch.save(st, 'model_vae_3.tar') Вначале создаем модель и набор обучающих данных. Затем выбираем оптимизатор, создаем функцию потерь в виде экземпляра класса VAELoss, указываем пять эпох обучения и переводим модель в режим обучения. После этого идет стандартный цикл обучения модели и ее последующего сохранения. Давайте посмотрим на полученное распределение векторов скрытого состояния h. Для этого переведем модель в режим эксплуатации, воспользуемся тестовым набором изображений MNIST и с помощью модели вычислим векторы скрытого состояния для всей выборки: model.eval() d_test = torchvision.datasets.MNIST(r'C:\datasets\mnist', download=True, train=False, transform=transforms) x_data = transforms(d_test.data).view(len(d_test), -1) _, h, _, _ = model(x_data) h = h.detach().numpy() plt.scatter(h[:, 0], h[:, 1]) plt.grid() plt.show() После запуска программы получим следующий результат:
Как видите, распределение получилось близкое к требуемому. Теперь, мы можем брать любые точки из этого пространства и должны при этом получать осмысленные изображения. Проверим это. В квадрате (-3;3) возьмем равномерно точки и подадим на вход декодера: n = 5 total = 2*n+1 plt.figure(figsize=(total, total)) num = 1 for i in range(-n, n+1): for j in range(-n, n+1): ax = plt.subplot(total, total, num) num += 1 h = torch.tensor([3*i/n, 3*j/n], dtype=torch.float32) predict = model.decoder(h.unsqueeze(0)) predict = predict.detach().squeeze(0).view(28, 28) dec_img = predict.numpy() plt.imshow(dec_img, cmap='gray') ax.get_xaxis().set_visible(False) ax.get_yaxis().set_visible(False) plt.show() Увидим следующий набор изображений:
В верхнем правом углу образы получились не очень понятные. Это вполне возможно, так как в точке (3; 3) имеем самый край области и там могут быть неопределенные изображения. Также видим, что некоторые цифры отсутствуют, а некоторые изображения представляют собой переход из одной цифры в другую. Это вполне естественный результат, так как мы выбрали лишь некоторые из точек пространства, которые расположены в областях строго определенных цифр. При этом сами цифры группируются в пространстве векторов скрытого состояния. Мы можем выделять группы из семерок, единиц, нулей. Чтобы знать, какая область отвечает за генерацию изображения той или иной цифры, достаточно вычислить ее среднее значение и дисперсию с помощью модели кодера: x_data = d_train.data[d_train.targets == 1] batch_size = x_data.size(0) x_data = transforms(x_data).view(batch_size, -1) enc = model.encoder(x_data) h_mean, h_log_var = model.h_mean(enc), model.h_log_var(enc) h_mean = torch.mean(h_mean, dim=0) h_std = torch.mean(torch.exp(h_log_var / 2), dim=0) n = 5 total = 2*n+1 plt.figure(figsize=(total, total)) num = 1 for i in range(-n, n+1): for j in range(-n, n+1): ax = plt.subplot(total, total, num) num += 1 h = torch.tensor([3 * h_std[0] * i/n + h_mean[0], 3 * h_std[1] * j/n + h_mean[1]], dtype=torch.float32) predict = model.decoder(h.unsqueeze(0)) predict = predict.detach().squeeze(0).view(28, 28) dec_img = predict.numpy() plt.imshow(dec_img, cmap='gray') ax.get_xaxis().set_visible(False) ax.get_yaxis().set_visible(False) plt.show() После запуска увидим различные изображения единиц:
Правда, не всем цифрам так «повезло». Если, например, взять цифру пять, то получим следующий набор:
Совсем не очень! Конечно, здесь еще можно улучшить саму модель автоэнкодера и дольше его обучать. Но на следующем занятии мы увидим другой прием, позволяющий успешно генерировать строго указанные изображения. Курс по нейронным сетям: https://stepik.org/a/227582 Видео по теме |