|
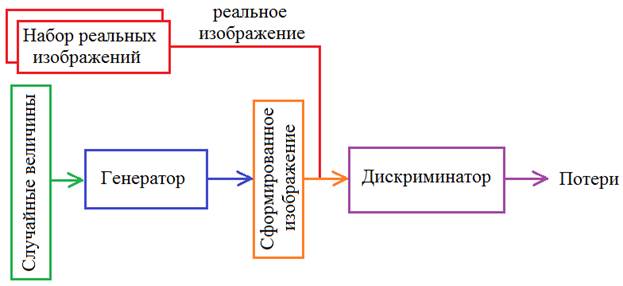
Реализация GAN на PyTorchКурс по нейронным сетям: https://stepik.org/a/227582 На предыдущем занятии мы с вами рассмотрели общую концепцию генеративно-состязательных сетей (GAN). Теперь, пришло время ее реализовать. И сделаем это с помощью фреймворка PyTorch. Схема генеративно-состязательной сети, которую мы будем создавать, будет следующей:
Чтобы генератор лучше формировал изображения, их следует взять однотипными, например, все пятерки. Для этого создадим класс Dataset, возвращающий изображения пятерок из БД MNIST: class DigitDataset(data.Dataset): def __init__(self, path, train=True, target=5, transform=None): _dataset = torchvision.datasets.MNIST(path, download=True, train=train) self.dataset = _dataset.data[_dataset.targets == target] self.length = self.dataset.size(0) self.target = torch.tensor([target], dtype=torch.float32) if transform: self.dataset = transform(self.dataset).view(-1, 1, 28, 28) def __getitem__(self, item): return self.dataset[item], self.target def __len__(self): return self.length В инициализатор передается маршрут к БД MNIST, тип выборки (обучающая или тестовая), целевое значение для отбора однотипных изображений (по умолчанию пятерок) и трансформации, которые применяются ко всей выборке. После этого происходит загрузка БД MNIST, выделение из нее только целевых изображений с применением указанных трансформаций. В методе __getitem__ возвращается один образ выборки по индексу item, а метод __len__ возвращает размер всей обучающей выборки. Непосредственное создание обучающей выборки выполняется следующими командами: transforms = tfs_v2.Compose([tfs_v2.ToImage(), tfs_v2.ToDtype(dtype=torch.float32, scale=True)]) d_train = DigitDataset(r'C:\datasets\mnist', train=True, transform=transforms) train_data = data.DataLoader(d_train, batch_size=batch_size, shuffle=True, drop_last=True) Здесь все вам должно быть знакомо, и напомню, что параметр drop_last=True отбрасывает последний мини-батч, т.к. он может быть меньшего размера, чем все остальные. Обучающая выборка готова. Следующим шагом опишем модели генератора и дискриминатора. И, так как, мы работаем с изображениями, то воспользуемся сверточными слоями: - модель генератора: model_gen = nn.Sequential( nn.Linear(2, 512*7*7, bias=False), nn.ELU(inplace=True), nn.BatchNorm1d(512*7*7), nn.Unflatten(1, (512, 7, 7)), nn.Conv2d(512, 256, 5, 1, padding='same', bias=False), nn.ELU(inplace=True), nn.BatchNorm2d(256), nn.Conv2d(256, 128, 5, 1, padding='same', bias=False), nn.ELU(inplace=True), nn.BatchNorm2d(128), nn.ConvTranspose2d(128, 64, 4, 2, padding=1, bias=False), nn.ELU(inplace=True), nn.BatchNorm2d(64), nn.ConvTranspose2d(64, 32, 4, 2, padding=1, bias=False), nn.ELU(inplace=True), nn.BatchNorm2d(32), nn.Conv2d(32, 1, 1, 1), nn.Sigmoid() ) - модель дискриминатора: model_dis = nn.Sequential( nn.Conv2d(1, 64, 5, 2, padding=2, bias=False), nn.ELU(inplace=True), nn.BatchNorm2d(64), nn.Conv2d(64, 128, 5, 2, padding=2, bias=False), nn.ELU(inplace=True), nn.BatchNorm2d(128), nn.Flatten(), nn.Linear(128*7*7, 1), ) Все используемые здесь классы мы уже много раз применяли и вам они уже должны быть знакомы. Кроме, может быть, класса nn.Unflatten, который преобразует вектор в многомерный тензор с указанными размерностями. Первый аргумент – номер преобразуемой оси, второй – новая размерность указанной оси. В результате класс: nn.Unflatten(1, (512, 7, 7)) вторую ось (dim=1) превращает в трехмерную матрицу размерностью (512, 7, 7). Также обратите внимание, что на входе генератор будет ожидать двумерный вектор из независимых нормальных СВ, размерностью hidden_dim:
Поэтому в первом полносвязном слое указана входная размерность 2. На вход дискриминатора будут подаваться изображения размером 28х28 пикселей, а на выходе формироваться одно числовое значение, которое можно воспринимать, как уверенность дискриминатора в натуральности поданного изображения. После определения моделей переведем их на графический процессор, так как подобные сети обучаются, как правило, достаточно долго: device = torch.device("cuda" if torch.cuda.is_available() else "cpu") print(device) model_gen.to(device) model_dis.to(device) Далее, сразу зададим число эпох обучения, размерность вектора для генератора и размер мини-батча: epochs = 20 hidden_dim = 2 batch_size = 16 Затем, нам понадобятся два отдельных оптимизатора для генератора и дискриминатора: optimizer_gen = optim.Adam(params=model_gen.parameters(), lr=0.001) optimizer_dis = optim.Adam(params=model_dis.parameters(), lr=0.001) и функция потерь в виде бинарной кросс-энтропии: loss_func = nn.BCEWithLogitsLoss() Для обучения моделей заранее сформируем целевые значения для реальных и фейковых изображений в виде следующих тензоров: targets_0 = torch.zeros(batch_size, 1).to(device) targets_1 = torch.ones(batch_size, 1).to(device) а также списки для хранения истории изменения функций потерь для генератора и дискриминатора: loss_gen_lst = [] loss_dis_lst = [] Переводим модели в режим обучения: model_gen.train() model_dis.train() и описываем главный цикл обучения следующим образом: for _e in range(epochs): loss_mean_gen = 0 loss_mean_dis = 0 lm_count = 0 train_tqdm = tqdm(train_data, leave=True) for x_train, y_train in train_tqdm: x_train = x_train.to(device) h = torch.normal(mean=torch.zeros((batch_size, hidden_dim)), std=torch.ones((batch_size, hidden_dim))) h = h.to(device) img_gen = model_gen(h) fake_out = model_dis(img_gen) loss_gen = loss_func(fake_out, targets_1) optimizer_gen.zero_grad() loss_gen.backward() optimizer_gen.step() # discriminator learning img_gen = model_gen(h) fake_out = model_dis(img_gen) real_out = model_dis(x_train) outputs = torch.cat([real_out, fake_out], dim=0).to(device) targets = torch.cat([targets_1, targets_0], dim=0).to(device) loss_dis = loss_func(outputs, targets) optimizer_dis.zero_grad() loss_dis.backward() optimizer_dis.step() lm_count += 1 loss_mean_gen = 1/lm_count * loss_gen.item() + (1 - 1/lm_count) * loss_mean_gen loss_mean_dis = 1/lm_count * loss_dis.item() + (1 - 1/lm_count) * loss_mean_dis train_tqdm.set_description(f"Epoch [{_e+1}/{epochs}], loss_mean_gen={loss_mean_gen:.3f}, loss_mean_dis={loss_mean_dis:.3f}") loss_gen_lst.append(loss_mean_gen) loss_dis_lst.append(loss_mean_dis) Смотрите, для каждого очередного мини-батча вначале делается обучение генератора. Для этого на его вход подается тензор с двумя нормально распределенными случайными величинами (единичной дисперсией и нулевым средним). Выходное изображение сохраняется в переменной img_gen. Затем, сформированное изображение подается на дискриминатор, который выдает некоторый прогноз. Он сохраняется в переменной fake_out. Нам необходимо, обучить генератор так, чтобы дискриминатор решил, что это реальное изображение. Следовательно, целевое значение бинарной кросс-энтропии для генератора должно быть 1. Это означало бы, что дискриминатор не смог отличить сгенерированное изображение от реального. И, затем, делается один шаг градиентного спуска для обучения только генератора. Следом идет обучение дискриминатора на том же самом мини-батче. Необходимо снова пропустить тензор h через генератор, чтобы PyTorch заново выстроил вычислительный граф, т.к. после ранее вызванного метода backward он фиксируется и второй раз по нему пройтись уже не получится. Затем, через дискриминатор пропускаем сгенерированные изображения (в пределах мини-батча) и отдельно реальные изображения. Полученные выходные значения объединяем в единый тензор по первой оси (по батчам). И то же самое делаем для целевых значений (это можно вынести за пределы цикла обучения). Причем, для реальных изображений будем требовать на выходе единицы, а для сгенерированных – нули. Так дискриминатор должен отличать фейковые изображения от реальных. После этого делается один шаг обучения, минимизируя его функцию потерь. В конце вычисляются для генератора и дискриминатора средние значения потерь, выводится служебная информация на экран с сохранением их в соответствующие списки. После обучения сохраним модели и историю обучения: st = model_gen.state_dict() torch.save(st, 'model_gen.tar') st = model_dis.state_dict() torch.save(st, 'model_dis.tar') st = {'loss_gen': loss_gen_lst, 'loss_dis': loss_dis_lst} torch.save(st, 'model_gan_losses.tar') И, наконец, выведем на экран результаты генерации изображений: model_gen.eval() n = 2 total = 2*n+1 plt.figure(figsize=(total, total)) num = 1 for i in range(-n, n+1): for j in range(-n, n+1): ax = plt.subplot(total, total, num) num += 1 h = torch.tensor([[1 * i / n, 1 * j / n]], dtype=torch.float32) predict = model_gen(h.to(device)) predict = predict.detach().squeeze() dec_img = predict.cpu().numpy() plt.imshow(dec_img, cmap='gray') ax.get_xaxis().set_visible(False) ax.get_yaxis().set_visible(False) plt.show() После запуска программы и обучения GAN увидим следующий результат генерации изображений пятерок:
Как видим, получаются вполне четкие не смазанные изображения пятерок. Это как раз то, к чему мы стремились. Теперь, обученный генератор можно использовать отдельно для формирования таких изображений. Генеративно-состязательные сети, как правило, долго обучаются в сравнении с обычными сетями. Здесь нам приходится подстраивать весовые коэффициенты отдельно для дискриминатора, затем для генератора и это конкурирующее обучение необходимо повторять много раз для достижения приемлемых результатов. Поэтому число эпох вполне может достигать 100 и более. Дополнительные сложности при обучении возникают из-за взаимного влияния дискриминатора и генератора друг на друга. Вполне может возникнуть ситуация, когда градиенты генератора будут близки к нулю и обучение попадает в некую ловушку, когда недообученный дискриминатор хорошо различает фейковые изображения недообученного генератора. При этом генератор дальше не обучается из-за этих малых градиентов. Но все это можно преодолеть при грамотном подходе к обучению. Вот так в самом простом случае можно реализовать и обучить генеративно-состязательную сеть для формирования реалистичных изображений цифр. И я думаю, что вы теперь в целом понимаете принцип построения и обучения генеративных сетей. Курс по нейронным сетям: https://stepik.org/a/227582 Видео по теме |