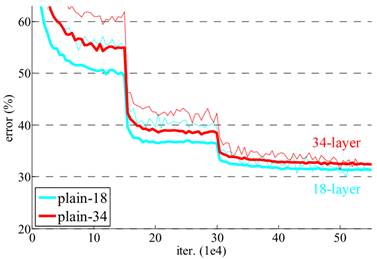
|
Остаточные нейронные сети (residual networks - ResNet)На прошлых занятиях мы с вами подробно познакомились с VGG-сетями, которые содержат 11, 13, 16 или 19 слоев. Последние две можно определенно отнести к глубоким НС. Конечно, увеличение числа слоев – это не просто прихоть разработчика, глубокие сети лучше справляются с решением сложных задач, например, классификации реальных полноцветных изображений. В частности, на конкурсе ImageNet лучшие результаты показывают сети с сотнями и даже тысячами слоев. И, кажется, мы теперь знаем, как их построить? Если есть сети VGG-16 и VGG-19, то по аналогии давайте создадим сети VGG-23, VGG-35 и так далее? Вначале так и сделали. Но оказалось, что сети, содержащие более 20 слоев, ведут себя также или даже показывают худшие результаты, чем аналогичная сеть VGG-19. Вот, ставший уже классическим, график качества классификации в ImageNet сетей с 18 и 34 слоями (названия: plain-18 и plain-34):
Видим, что сети с 34 слоями, в среднем, проигрывают сетям с 18 слоями. Почему так происходит? Исследования показали, что если взять НС с большим числом слоев и применить к ней алгоритм обратного распространения ошибки (back propagation), то обучение будет проходить неравномерно. Последние слои (те, что ближе к выходу) будут обучаться быстрее начальных. В результате, ошибка на выходе будет стремиться к нулю и, как следствие, градиенты также будут принимать малые значения. А величина градиента, как мы знаем, влияет на величину изменения весовых коэффициентов, согласно общей формуле градиентного спуска:
Это значит, что хорошо обученные последние слои «блокируют» обучение начальных слоев и алгоритм обратного распространения, фактически, застревает на определенном уровне, как правило, далеко не оптимальном. Все это теперь известно под названием проблема затухающих (исчезающих) градиентов (vanishing gradients). Одно из первых решений преодоления проблем с градиентами стало предобучение фрагментов глубокой нейронной сети. Грубо говоря, вся сеть разбивалась на несколько независимых частей, каждая часть представляла собой уже обычную не глубокую нейронную сеть и могла быть обучена до некоторого начального уровня. При этом использовался метод обучения без учителя, например, на основе ограниченных машин Больцмана (так делала группа под руководством британского ученого Джеффри Хинтона). А, затем, запускался алгоритм дообучения для всей сети стандартным способом.
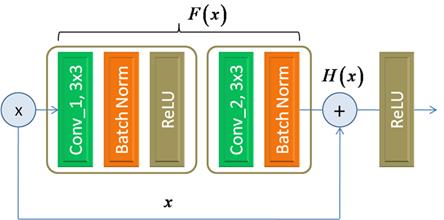
Джеффри Хинтон Однако сейчас эта техника почти не используется, но она позволила лучше понять направления дальнейших исследований для поиска решений обучения глубоких сетей. Как результат, были предложены эффективные методы начальной инициализации весов, благодаря работам Ян ЛеКуна, Йошуа Бенджи и Хавьера Глоро. А два сотрудника Google Иоффе и Сегеди в 2015-м предложили алгоритм батч-нормализации (Batch Normalization) для ускорения сходимости алгоритма градиентного спуска. Благодаря этим разработкам, а также различным оптимизаторам самого градиентного алгоритма, проблема исчезающих градиентов отошла на второй план. Остаточные нейронные сети (residual networks)Несмотря на то, что все эти наработки позволили лучше и быстрее обучать небольшие по глубине НС, проблема обучения по настоящему глубоких НС все еще оставалась неразрешенной. Первые попытки преодолеть проклятие глубины путем подбора подходящих архитектур, привели к появлению сетей семейства Inception от корпорации Google. Но в 2015-году китайское подразделение Microsoft Research предложило поистине революционную идею формирования архитектур очень глубоких НС. Как и все гениальное, мысль оказалась предельно простой. Китайские инженеры предложили несколько подряд идущих сверточных слоев обходить напрямую, связывая их вход с выходом, например, так:
Здесь входной тензор x поступает на первый сверточный слой Conv_1, проходит через блоки Batch Normalization и функцию активации ReLU, после чего выходной сигнал обрабатывается следующим сверточным слоем Conv_2 с последующим блоком Batch Normalization. Но параллельно тензор x напрямую пропускается, минуя оба сверточных слоя. На выходе формируется сигнал:
который пропускается через функцию активации ReLU. Впоследствии такой блок получил название Basic Block (основной, базовый блок). А связь, которая напрямую связывает вход с выходом, по-английски называется skip connection, а по-русски – прямая связь либо обходная связь. Но что такого особенного дает обходная связь? Давайте разберемся. Вначале вспомним, что любая НС (или ее фрагмент) – это, по сути, нелинейная функция, которая связывает входы с выходом:
И зависит от
набора весовых коэффициентов W. Предположим, что наш блок должен
воспроизводить нелинейную функцию
Отсюда и пошло
название таких моделей – остаточные сети (residual networks), сокращенно
ResNet. А блок,
соответственно, называют остаточным блоком. В таком блоке достаточно
обучить сеть воспроизводить не весь сигнал целиком, а лишь отличия входных
значений для получения требуемой функции
Благодаря единичке, которая появляется за счет «обходного» пути, градиент не будет затухать при распространении от последних слоев к начальным и сеть, сколь большой бы она не была, будет обучаться равномерно по всем слоям. Это одна из ключевых особенностей предложенной архитектуры, которая способствует построению и последующему обучению очень глубоких НС – от сотен слоев и более. Китайский ученый Каймин Хэ назвал это «революцией глубины». В сетях VGG-16 и VGG-19 было всего 16 и 19 слоев. Сеть GoogLeNet содержала 22 слоя, а в первом варианте ResNet – сразу 152 слоя. Сейчас это число доходит до нескольких тысяч уровней в глубину. И это не просто набор слоев, которые мы можем обучать. Они позволяют получать недостижимые ранее результаты. Например, в задачах распознавания образов, как правило, используют тот или иной вариант модификации сети ResNet. Мало того, такие блоки с обходной связью стали применять и в других архитектурах, например, Inception, значительно повышая качество их работы. Особенности Basic BlockПрежде чем переходить непосредственно к рассмотрению общей архитектуры сетей ResNet, завершим краткий обзор остаточных блоков. Вы, наверное, обратили внимание, что Basic Block содержит два сверточных слоя с вынесенным последним блоком функции активации ReLU после операции суммирования. И это не случайно. Практика показала, что обходная связь, охватывающая от двух и более сверточных слоев, работает заметно эффективнее, чем при охвате всего одного слоя. Поэтому в базовом блоке используется минимальное число необходимых сверточных слоев для построения эффективных архитектур. А вот насчет использования нелинейного слоя ReLU (либо другой подходящей нелинейной функции) после суммирования тензоров ряд исследователей высказывают сомнения. Например, сами авторы ResNet отмечают, что это не совсем правильный подход и лучше применять функции активации к тензорам перед их суммированием:
В этом случае выходное значение остаточного блока не подвергается никаким преобразованиям и оно в неизменном виде подается на следующий подобный блок. Математически можно показать, что градиент по K таким блокам будет иметь вид:
То есть, он с очень большой вероятностью не будет затухать, а значит, все слои глубокой сети будут обучаться примерно одинаково. А вот для блоков с вынесенной нелинейностью, для простоты пусть она описывается выражением:
получаем градиент в виде:
Если
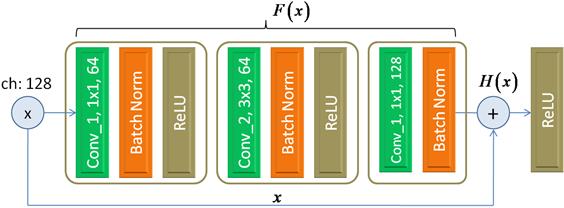
коэффициенты Bottleneck блокРассмотренный Basic Block далеко не единственный и не самый распространенный вариант. Чаще всего на практике используют другой, под названием Bottleneck Block (бутылочное горлышко). Его структура имеет следующий вид:
Для ясности здесь дополнительно указано число каналов входного тензора и число каналов с выхода каждого сверточного слоя. Это важная информация для понимания работы данного блока. Итак, входной тензор, состоящий, например, из 128 каналов подается на первый сверточный слой с 64 ядрами размером 1x1. Казалось бы, какая может быть польза от слоя с ядрами 1x1? Они же не способны анализировать соседние элементы входного сигнала и выделять значимые признаки? Так и есть. Назначение этого слоя в другом. Он сжимает число каналов входного тензора в два раза до 64, оставляя наиболее важные. И это свойство он приобретает в процессе обучения НС. Для чего потребовалось сжимать тензор по каналам? В данном случае для сокращения числа арифметических операций. Если на следующий сверточный слой с фильтрами 3x3 подать тензор с 64 каналами, то число операций на один элемент тензора составит: 3 * 3 * 64 * 64 = 36864 А если бы обрабатывался тензор со 128 каналами, то число операций было бы равно: 3 * 3 * 128 * 128 = 147456 В четыре раза больше! Всего же Bottleneck блок в трех сверточных слоях будет выполнять:
арифметических операций в расчете на один элемент входного тензора. Это почти в три раза меньше значения 147456 для одного сверточного слоя, напрямую обрабатывающий тензор со 128 каналами. При этом первый сверточный слой можно воспринимать, как сжимающий для формирования 64 каналов, а третий – как восстанавливающий исходную размерность в 128 каналов. Практика показала, что сети, построенные на Bottleneck блоках, как правило, дают лучшие или сравнимые результаты с блоками Basic и при этом содержат заметно меньше настраиваемых параметров, что ускоряет процесс обучения сети в целом. На следующем занятии мы с вами рассмотрим архитектуры сетей ResNet-18 и 50, построенных на базе блоков Basic и Bottleneck. Видео по теме |
.
Тогда набор сверточных слоев должен аппроксимировать лишь остаток функции 
гораздо проще,
чем исходную 
будут,
в среднем, меньше единицы, то градиент снова может затухать, а если больше
единицы, то экспоненциально возрастать. То есть, возникает дополнительная
нестабильность при обучении такой сети. Однако, благодаря использованию именно
функции ReLU, у которой
производная равна 1 для положительных значений, коэффициенты 
