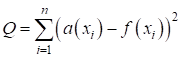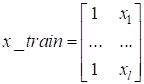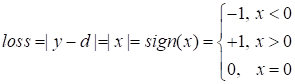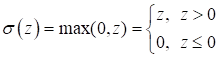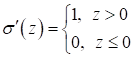|
Оптимизаторы. Реализация SGD на PyTorchНа предыдущем
занятии мы увидели, как в PyTorch происходит вычисление
производных для тензорных операций. Давайте применим этот механизм для
реализации стохастического градиентного спуска нахождения параметров
Пусть для
примера модель
То есть, будем
искать такие значения вектора
По сути, здесь используется квадратическая функция потерь. Реализацию этой задачи с помощью SGD на PyTorch можно выполнить следующим образом: neuro_net_15_sgd.py: https://github.com/selfedu-rus/neuro-pytorch/ Вначале формируется обучающая выборка: N = 2 w = torch.FloatTensor(N).uniform_(-1e-5, 1e-5) w.requires_grad_(True) x = torch.arange(0, 3, 0.1) y_train = 0.5 * x + 0.2 * torch.sin(2*x) - 3.0 x_train = torch.tensor([[_x ** _n for _n in range(N)] for _x in x]) Здесь y_train – это тензор со значениями функции в точках x, а x_train – двумерный тензор вида:
Скалярное
произведение строк этой матрицы на вектор
Далее идет цикл работы SGD: for _ in range(1000): k = randint(0, total-1) y = model(x_train[k], w) loss = (y - y_train[k]) ** 2 loss.backward() w.data = w.data - lr * w.grad w.grad.zero_() На каждой
итерации случайным образом выбирается образ из выборки x_train, вычисляется по
модели выходное значение y, а потом применяется квадратическая
функция потерь loss. Относительно этой функции вычисляются градиенты
для вектора
После этого нам обязательно нужно обнулить вычисленные градиенты, иначе новые будут добавлены к существующим. Результатом работы этой программы будут следующие коэффициенты: tensor([-2.8083, 0.3659]) и модель достаточно хорошо описывает данные обучающей выборки. Конечно, в качестве квадратической функции потерь в программе можно воспользоваться готовым классом MSELoss. Сначала создается объект этого класса: loss_func = torch.nn.MSELoss() А затем, loss_func в цикле вызывается с двумя аргументами: loss = loss_func(y, y_train[k]) # аналог loss = (y - y_train[k]) ** 2 Получим тот же результат работы программы. Оптимизаторы градиентного спускаКонечно, в чистом виде стохастический градиентный спуск практически никогда не используется. На это есть, по крайней мере, две веские причины. Первая – застревание в локальных минимумах функционала качества (функции потерь). И вторая – сложность подбора и изменения шага обучения на каждой итерации. Для решения этих проблем было придумано множество эвристик, которые известны, как оптимизаторы градиентных алгоритмов. Подробно мы о них говорили на курсе по машинному обучению. Здесь приведу лишь основные из них с краткой характеристикой:
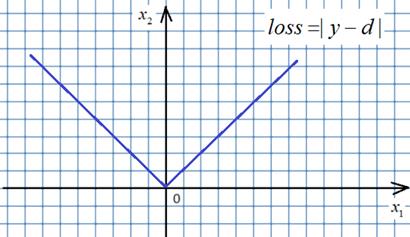
Конечно, это не все существующие оптимизаторы. Их огромное количество, каждый для своих задач. Здесь приведены наиболее часто используемые, которые хорошо себя зарекомендовали при обучении самых разных НС. Но остается вопрос, какой оптимизатор выбрать? Общая рекомендация здесь такая. Часто вначале применяют оптимизатор Adam. Он показывает хорошие результаты для широкого спектра задач и архитектур НС. Затем, если результат не удовлетворяет, можно попробовать RMSprop и NAdam. Наконец, можно попробовать применить оптимизатор с импульсом Нестерова. Но, опять же, какой оптимизатор окажется лучшим и какие параметры ему следует передать, зависит от конкретной решаемой задачи и опыта разработчика. Давайте добавим оптимизатор «импульс Нестерова» для SGD. Вначале импортируем ветку: import torch.optim as optim где расположены различные оптимизаторы, а затем, создадим нужный с помощью команды: optimizer = optim.SGD(params=[w], lr=0.01, momentum=0.8, nesterov=True) Обратите внимание, что здесь шаг обучения lr задается одним вещественным числом. Далее, он может автоматически изменяться внутри самого оптимизатора. Кроме того, изменяемые параметры w должны передаваться в списке или в другом допустимом итерированном объекте, например, кортеже, множестве. Но, обычно, используется список, как наиболее удобный вариант. После создания оптимизатора цикл работы алгоритма SGD можно записать в следующем виде: for _ in range(1000): k = randint(0, total-1) y = model(x_train[k], w) loss = loss_func(y, y_train[k]) loss.backward() # w.data = w.data - lr * w.grad # w.grad.zero_() optimizer.step() optimizer.zero_grad() По сути, заменяются две последние строчки, где выполняется шаг градиентного спуска. Здесь команда: optimizer.step() автоматически изменяет веса с вычисленным шагом обучения и указанным оптимизатором. А команда: optimizer.zero_grad() обнуляет вычисленные градиенты для указанного списка параметров w. Давайте для примера создадим другой оптимизатор. Пусть это будет Adam: optimizer = optim.Adam(params=[w], lr=0.01) И изменим функцию потерь на модуль разности: loss_func = torch.nn.L1Loss() Все, теперь алгоритм SGD использует указанный оптимизатор и другую функцию потерь. Видите, все делается очень просто. У некоторых из вас может возникнуть вопрос. А как может быть применена функция потерь вида:
Она же в точке 0 не имеет производной? Да, это так. Но алгоритм градиентного спуска не требует аналитического значения производных. Ему достаточно указать значение производной до и после точки 0, а в нуле просто приравнять нулю:
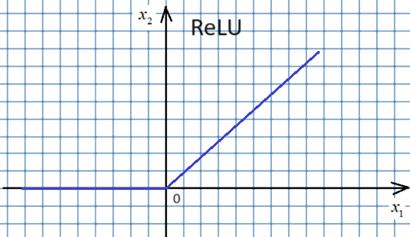
Это возможно, так как градиентный алгоритм – это численный метод оптимизации. Аналитических решений мы с его помощью не ищем, а лишь приближенные численные значения оптимизируемых параметров. По той же причине функция активация ReLU:
может восприниматься, как дифференцируемая функция с производной вида:
И так для всех подобных функций, которые могут аналитически быть не дифференцируемыми, но заменены на соответствующие аналоги и далее применяться в численных алгоритмах. Видео по теме |
следующей
линейной модели:
аппроксимирует
функцию вида:
и
корректируются по алгоритму градиентного спуска:
