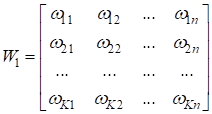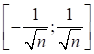|
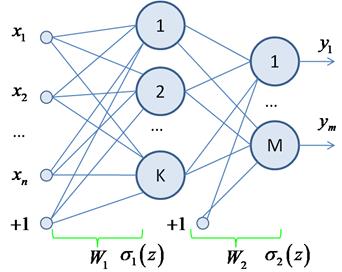
Классы nn.Linear и nn.ModuleКурс по нейронным сетям: https://stepik.org/a/227582 На предыдущих занятиях мы с вами выяснили, что работу одного полносвязного слоя НС прямого распространения можно описать одним математическим выражением:
где
И так как это типовой слой НС, то фреймворк PyTorch содержит специальный класс: torch.nn.Linear который автоматизирует вычисления формулы:
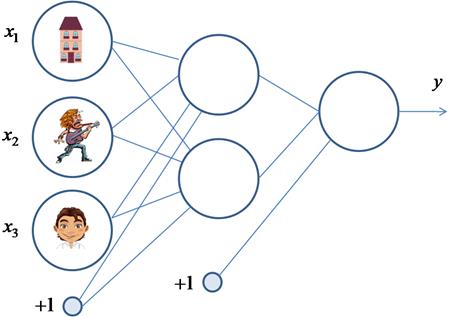
Класс nn.LinearДавайте представим, что мы бы хотели описать работу уже знакомой нам НС с использованием класса nn.Linear. Эта сеть состоит из двух полносвязных слоев, следовательно, нам необходимо сформировать два объекта следующими командами: import torch import torch.nn as nn import torch.nn.functional as F layer1 = nn.Linear(in_features=3, out_features=2) layer2 = nn.Linear(2, 1) Аргумент in_features=3 указывает размер входного вектора (без учета bias), а аргумент out_features=2 – размер выходного вектора.
У нашей НС, как раз, три входа на первом слое и должно формироваться два выхода у соответствующих нейронов скрытого слоя. Второй (выходной) слой принимает вектор из двух компонент (без учета bias) и формирует одно выходное значение. Именно поэтому были указаны аргументы 2 и 1. Следующим шагом давайте объявим функцию с именем forward, которая будет пропускать через НС входной вектор inp: def forward(inp, l1: nn.Linear, l2: nn.Linear): u1 = l1.forward(inp) s1 = F.tanh(u1) u2 = l2.forward(s1) s2 = F.tanh(u2) return s2 Смотрите, каждый объект класса nn.Linear имеет метод forward, который вычисляет выходное значение по формуле:
Но нам нужно полученный вектор u1 еще пропустить через функцию активации. Выберем также гиперболический тангенс. Поэтому следом идет команда: s1 = F.tanh(u1) Это и есть вектор (тензор) выходных значений нейронов скрытого слоя. Вычисленные значения s1, в свою очередь, подаются на следующий выходной слой и по аналогии вычисляется выходное значение s2 НС. Все очень просто. По умолчанию весовые коэффициенты и смещения инициализируются случайными значениями по равномерному закону с нулевым средним в диапазоне:
где n – количество признаков (размерность входных данных). Значения параметров можно посмотреть в следующих свойствах: layer1.weight layer2.weight layer1.bias layer2.bias Давайте проверим, как будет работать функция forward. Для этого текущие весовые коэффициенты объектов layer1 и layer2, а также их bias установим такими, которые были получены при обучении НС алгоритмом back propagation: layer1.weight.data = torch.tensor([[0.7402, 0.6008, -1.3340], [0.2098, 0.4537, -0.7692]]) layer1.bias.data = torch.tensor([0.5505, 0.3719]) layer2.weight.data = torch.tensor([[-2.0719, -0.9485]]) layer2.bias.data = torch.tensor([-0.1461]) Теперь, пропуская через эту сеть вектор x: x = torch.FloatTensor([1, -1, 1]) y = forward(x, layer1, layer2) print(y.data) будем получать выходные значения, близкие к 1 и -1. Как видите, наша НС работает корректно. Класс nn.ModuleКонечно, описывать работу всей НС или ее части через функции, не самый лучший подход. Гораздо удобнее использовать класс и в нем формировать всю необходимую логику. Тем более что фреймворк PyTorch предоставляет для этого специальный класс: torch.nn.Module То есть, мы можем создавать свои собственные модули нейронных сетей, которые будут на программном уровне работать, как единое целое. Давайте посмотрим, как это делается. В самом простом варианте достаточно объявить свой собственный класс (например, с именем MyModule или каким-либо другим) унаследованный от базового класса nn.Module, и внутри класса определить два метода:
class MyModule(nn.Module): def __init__(self, список передаваемых параметров при создании модуля): super().__init__() # вызов инициализатора базового класса # создание и инициализация переменных модуля def forward(self, x): # реализация прямого прохода вектора x по нейронной сети return # возврат тензора с выходными значениями нейронной сети Например, для описания работы нашей НС класс модуля можно записать следующим образом: class NetGirl(nn.Module): def __init__(self, input_dim, num_hidden, output_dim): super().__init__() self.layer1 = nn.Linear(input_dim, num_hidden) self.layer2 = nn.Linear(num_hidden, output_dim) def forward(self, x): x = self.layer1(x) x = F.tanh(x) x = self.layer2(x) x = F.tanh(x) return x Здесь мы формируем два полносвязных слоя layer1 и layer2, а метод forward, по сути, повторяет прежнюю функцию forward. Все достаточно просто. Давайте теперь посмотрим, что нам это дает. Во-первых, мы легко можем создавать двухслойные полносвязные НС с произвольным числом нейронов скрытого и выходного слоев. Например: model = NetGirl(3, 2, 1) # число входов 3; число нейронов 2 и 1 model1 = NetGirl(3, 5, 2) # число входов 3; число нейронов 5 и 2 model2 = NetGirl(100, 18, 10) # число входов 100; число нейронов 18 и 10 Чтобы просмотреть компоненты, содержащиеся в текущем модуле, достаточно вызвать функцию print: print(model) Получим: NetGirl(
А для получения списка всех оптимизируемых параметров модели следует вызвать метод parameters: gen_p = model.parameters() # возвращает генератор с набором параметров print(list(model.parameters())) # отображение списка параметров Как видите, базовый класс nn.Module автоматизирует множество вспомогательных действий. Следующим шагом обучим НС model по уже знакомой нам выборке: x_train = torch.FloatTensor([(-1, -1, -1), (-1, -1, 1), (-1, 1, -1), (-1, 1, 1), (1, -1, -1), (1, -1, 1), (1, 1, -1), (1, 1, 1)]) y_train = torch.FloatTensor([-1, 1, -1, 1, -1, 1, -1, -1]) total = len(y_train) При обучении воспользуемся оптимизатором RMSProp и квадратической функцией потерь: optimizer = optim.RMSprop(params=model.parameters(), lr=0.01) loss_func = torch.nn.MSELoss() Обратите внимание, как легко и просто передать в оптимизатор набор подбираемых параметров. Достаточно вызвать метод parameters у соответствующей модели. Переведем модель в режим обучения: model.train() Для нашей простой модели режим train не будет играть никакой роли, т.к. сеть работает в одном единственном режиме. Но это бывает не всегда так. Как мы увидим далее, например, слой Dropout или BatchNormalization используют разные режимы в процессе обучения и в процессе эксплуатации. Поэтому правилом хорошего тона является вызов метода train перед обучением модели. Далее пропишем знакомый нам цикл алгоритма SGD в виде: for _ in range(1000): k = randint(0, total-1) y = model(x_train[k]) loss = loss_func(y, y_train[k]) optimizer.zero_grad() loss.backward() optimizer.step() Мы здесь на каждой итерации выбираем случайный образ из выборки. И на его основе вычисляем потери и делаем коррекцию всех весовых коэффициентов НС по алгоритму back propagation. Причем, вначале нужно обнулить все градиенты, только после этого выполнить метод backward, а затем, метод step. Порядок вызова этих методов важен. После цикла обучения переводим модель в режим эксплуатации: model.eval() и проверяем ее работу по обучающей выборке: for x, d in zip(x_train, y_train): y = model(x) print(f"Выходное значение НС: {y.data} => {d}") Получим примерно такой результат: Выходное
значение НС: tensor([-0.9862]) => -1.0
Как видите, сеть неплохо обучилась. А полученный программный код стал гораздо удобнее и универсальнее того, что мы писали при ручной реализации алгоритма back propagation. Например, можно легко изменить число нейронов на скрытом слое: model = NetGirl(3, 3, 1) и снова запустить процесс обучения. Получим новую модель с корректно подобранными весами. В этом и заключается универсальность программы. Однако сейчас, в процессе тестирования модели, тензоры с ее настраиваемыми параметрами имеют включенные градиенты (requires_grad=True). Это влечет за собой построение графа вычислений и дополнительные расходы памяти устройства. Чтобы локально в программе отключить градиенты и ускорить выполнение программы при тестировании модели, PyTorch предоставляет следующий контекстный менеджер: with torch.no_grad(): ... Воспользуемся им следующим образом: for x, d in zip(x_train, y_train): with torch.no_grad(): y = model(x) print(f"Выходное значение НС: {y.data} => {d}") Все операции внутри этого контекстного менеджера выполняются с выключенными градиентами. Конечно, для нашей простой модели это не играет особой роли. Но для больших моделей с множеством слоев и сотнями тысяч нейронов эта операция может заметно ускорить выполнение программы с немалой экономией памяти. Поэтому при тестировании моделей рекомендуется отключать поддержку локальных градиентов. Еще одним способом отключить градиенты параметров модели является вызов метода: model.requires_grad_(False) Но тогда следует не забыть их включить снова при обучении или дообучении НС командой: model.requires_grad_(True) Курс по нейронным сетям: https://stepik.org/a/227582 Видео по теме |