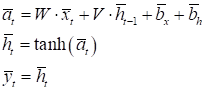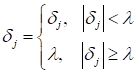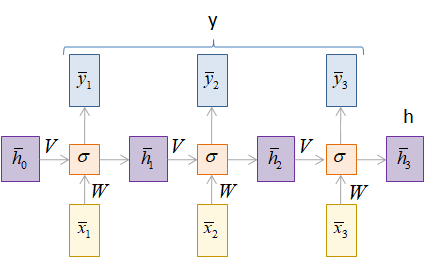
Рекуррентные нейронные сети
Введение в рекуррентные нейронные сети
Класс nn.RNN рекуррентного слоя
Рекуррентная сеть для прогноза символов
Понятие эмбеддинга. Embedding слов
Прогноз слов рекуррентной нейронной сетью
Функции активации в RNN. Двунаправленные (bidirectional) RNN-слои
Двунаправленные RNN в PyTorch. Сентимент-анализ фраз
LSTM - долгая краткосрочная память
Рекуррентный блок GRU
Обучающие курсы
Python Python ООП Django C/C++ ООП C++ Машинное обучение Структуры данных
Телеграм-каналы
Канал selfedu_rus Python Django Машинное обучение Java и С++
Наши каналы

Класс nn.RNN рекуррентного слоя

Смотреть материал на YouTube | RuTube

На предыдущем занятии мы в целом познакомились с рекуррентными НС. Давайте теперь сделаем следующий шаг и построим с помощью фреймворка PyTorch простую рекуррентную НС, на вход которой будем подавать отдельные символы, а на выходе требовать прогноз следующего символа:

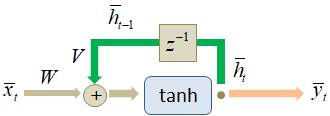
Но вначале нужно узнать, как реализуется рекуррентный слой в PyTorch. Для этого в ветке:

torch.nn

имеется класс, который так и называется RNN:

torch.nn.RNN

Этот класс описывает элмановскую архитектуру рекуррентного слоя с нелинейным преобразованием скрытого состояния (по умолчанию используется гиперболический тангенс):

Работу этого слоя можно описать следующими формулами:

То есть, матрицы W, V над стрелками умножаются на соответствующие векторы. Вы можете заметить, что здесь вектор скрытого состояния умножается на свою матрицу весов V. Это стандартный подход, который позволяет лучше контролировать итоговую сумму вектора с вектором .

Сам класс torch.nn.RNN содержит следующие основные параметры:

input_size – размер входного тензора;
hidden_size – размер вектора скрытого состояния;
num_layers=1 – число рекуррентных слоев;
nonlinearity='tanh' – функция активации;
bias=True – использование bias;
batch_first=False – формат входного тензора с первой осью batch_size

Последний параметр batch_first требует пояснений. По умолчанию размерности входного тензора описываются следующим образом:

(seq_length, batch_size, d_size)

где:

seq_length – длина подаваемой последовательности (число элементов);
batch_size – размер батча (мини-батча);
d_size – размер каждого подаваемого элемента последовательности.

Фактически параметр seq_length определяет число итераций в рекуррентном слое. Так вот, чтобы использовать тензоры с привычным нам порядком осей:

(batch_size, seq_length, d_size)

параметр batch_first нужно указывать со значением True.

Исчезающие и взрывающиеся градиенты

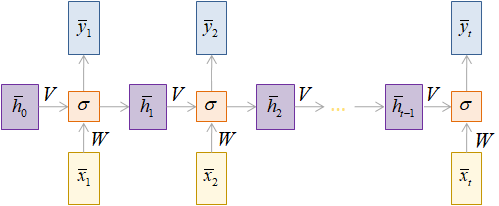
Давайте теперь посмотрим на развертку этого рекуррентного слоя во времени. Мы видим, что на каждом шаге вектор скрытого состояния умножается на матрицу весов V, а входной тензор – на матрицу W. Значения этих матриц легко могут оказаться такими, что даже при небольшой рекурсии (числе итераций) локальные градиенты достаточно быстро будут устремляться к нулю. Особенно, когда в качестве функции активации используется гиперболический тангенс или сигмоида. Получаем известную проблему исчезающих градиентов для рекуррентных слоев.

Надо сказать, что для элмановских RNN-слоев бороться с этой проблемой непросто. Во-первых, нужно правильно, аккуратно инициализировать матрицы W и V начальными значениями. Во-вторых, не использовать длинные входные последовательности, чтобы уменьшить число итераций в рекуррентном слое. Однако существует множество прикладных задач, где эти условия выполнить практически невозможно. Поэтому впоследствии были предложены более продвинутые архитектуры рекуррентных вычислений, в частности, LSTM и GRU, о которых речь еще впереди.

Итак, рекуррентные слои подвержены проблеме исчезающих градиентов. Несколько реже существует и обратная проблема, приводящая буквально к взрывному росту значений локальных градиентов. Однако побороть ее куда проще первой. В этом случае используется хорошо себя зарекомендовавшая эвристика обрезки больших по модулю градиентов некоторым пороговым значением:

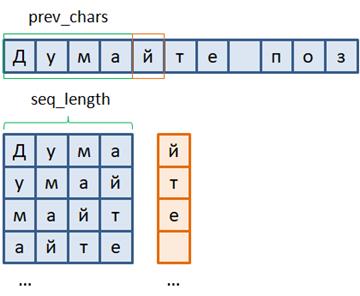
Все это следует учитывать при реализации алгоритма обучения рекуррентных слоев. А проблема их устойчивости – это отдельная научная задача.

Формат выборки для прогнозирования символов

Итак, как работают рекуррентные слои в PyTorch класса torch.nn.RNN мы с вами в целом разобрались. Давайте теперь рассмотрим формат входных данных для прогноза отдельных символов в предложениях, то есть формат обучающей выборки. Воспользуемся заранее заготовленным файлом train_data_true с короткими позитивными высказываниями. Как из него мы будем формировать обучающие данные? Смотрите. Для каждых предыдущих prev_chars символов сеть должна формировать прогноз текущего символа. В результате получаем следующий набор входных векторов и целевых значений:

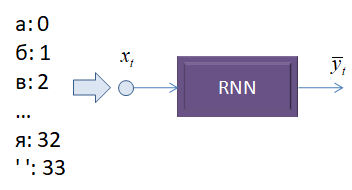
Обратите внимание, что количество подаваемых символов seq_length в каждом образе выборки будет определять число итераций в рекуррентном слое сети. А на выходе формироваться прогнозируемое значение. Получаем модель вида Many-to-One.

Далее нужно решить, в каком формате подавать символы последовательности на вход рекуррентного слоя. Первое, что приходит в голову – это каждому символу поставить в соответствие некое число и эти числа подавать на вход:

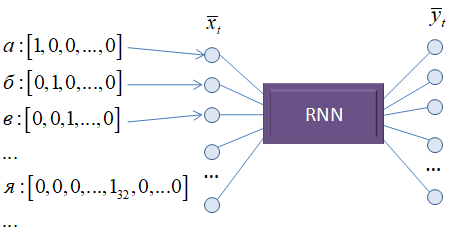
Это значило бы, что у нас есть один вход, который весовыми коэффициентами связан с нейронами скрытого слоя. Такая модель будет плохо различать символы, так как НС сложно интерпретировать числа как отдельные буквы. Гораздо лучшим решением будет связать строго определенный вход со строго определенным символом, например, так:

Здесь мы на вход подаем вектор длиной используемого алфавита с единицей на месте нужного символа. Благодаря этому НС сможет сформировать весовые коэффициенты независимо для каждой буквы, что гораздо лучше для их различения. Такое кодирование данных получило название:

One-hot encoding (OHE)

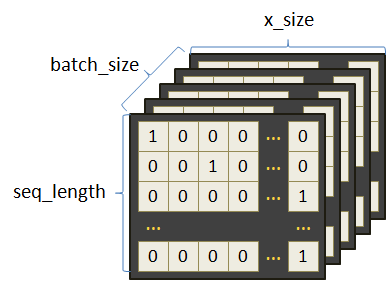
Именно его мы и будем использовать для представления входных символов. Выходной вектор будет иметь такой же формат данных. В результате тензор будет иметь следующий формат (batch_size, seq_length, d_size):

Применение класса nn.RNN

Итак, структура входных и выходных тензоров нами определена. Осталось выяснить, как на программном уровне применять класс nn.RNN фреймворка PyTorch.

Пусть на вход модели поступает тензор размерностью:

(batch_size, sq_length, d_size)

Тогда RNN-слой в самом простом случае может быть сформирован следующей командой:

rnn = nn.RNN(d_size, hidden_size, batch_first=True)

Здесь размер входных данных – это размер словаря d_size; размер hidden_size вектора скрытого состояния мы задаем самостоятельно, исходя из соображений решаемой задачи. Например, hidden_size можно взять 32, 64 или 128 и посмотреть, как сеть при этом будет строить прогноз. Последнее значение batch_first=True, как мы уже говорили, нужно указывать, если первая ось тензора содержит размер батча.

После создания объекта класса nn.RNN мы можем воспользоваться rnn-слоем, например, следующим образом:

import torch
import torch.nn as nn
 
rnn = nn.RNN(33, 64, batch_first=True)
 
x = torch.randn(8, 3, 33)
y, h = rnn(x)
 
print('y:', y.size())
print('h:', h.size())

В консоли увидим строчки:

y: torch.Size([8, 3, 64])
h: torch.Size([1, 8, 64])

Рекуррентный слой возвращает два тензора y и h. Тензор y содержит выходные значения на каждой итерации работы RNN-слоя, а тензор h – на последней итерации.

Остается вопрос, чему равен вектор начального состояния рекуррентного слоя? В PyTorch, если мы не указываем его явно, то он принимается нулевым. Однако, при необходимости, мы можем инициализировать его любыми числовыми значениями. Делается это следующим образом:

x = torch.randn(8, 3, 33)
h0 = torch.randn(1, 8, 64)
y, h = rnn(x, h0)

В данном примере тензор h0 принимает случайные значения, которые будут начальным состоянием вектора . Конечно, на практике, чаще всего оставляют нулевые значения. Это общепринятый подход.

На следующем занятии мы выполним непосредственную реализацию рекуррентной НС для прогнозов символов последовательности.

Класс nn.RNN рекуррентного слоя

Исчезающие и взрывающиеся градиенты

Формат выборки для прогнозирования символов

Применение класса nn.RNN

Видео по теме