|
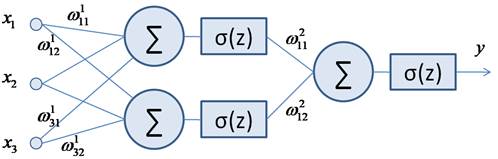
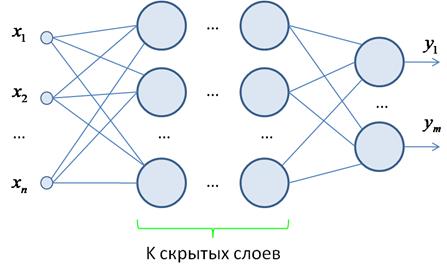
Идея обучения НС градиентным алгоритмомКурс по нейронным сетям: https://stepik.org/a/227582 На предыдущих занятиях мы с вами подробно познакомились с общей структурой полносвязной нейронной сети прямого распространения:
в которой использовалась исключительно пороговая функция активации:
и заранее
заданные весовые коэффициенты. Однако сразу указать нужные коэффициенты Одну и ту же
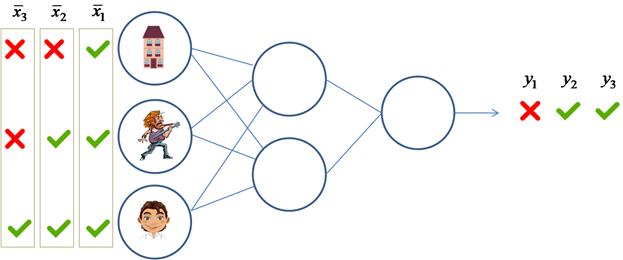
сеть можно обучить для самых разных задач. Например, классификации кошек и
собак, или классификации мужчин и женщин, или наличие и отсутствие аномалий на
рентгеновских снимках и так далее. Что конкретно будет делать сеть, зависит от
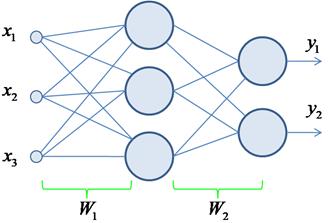
значений весов связей Пусть имеется следующая двухслойная сеть:
с набором весов
где:
Ту же самую формулу, можно кратко представить в виде:
или в более общей записи:
Здесь вектор Но что нам это дает? Смотрите. Если в нашем распоряжении будет множество различных входных данных:
с известными (требуемыми) выходными значениями:
то под эти
данные можно попытаться подобрать коэффициенты
Например, для
ранее рассмотренной НС, можно было бы сформировать матрицы Напомню, что в
общем случае набор данных Хорошо, у нас
имеется обучающая выборка, заданная структура нейронной сети, но как по этим
данным вычислять весовые коэффициенты Идея градиентного алгоритма обученияО градиентном
алгоритме я уже подробно рассказывал в курсе по машинному обучению. Поэтому
здесь углубляться в его работу не стану. Принцип заключается в следующем. Вначале
НС имеет некие, скорее всего, не подходящие значения весовых коэффициентов. И,
пропуская произвольный входной вектор
Для измерения
рассогласования между векторами
которая
минимальная (обычно 0), если векторы равны и увеличивается, при увеличении
рассогласования между Например, в задачах регрессии часто используется квадратическая функция потерь:
А в задачах бинарной (двухклассовой) классификации – бинарная кросс-энтропия:
где И так далее. Для каждой текущей задачи подбирается своя, наиболее подходящая функция потерь. Соответственно общий критерий качества работы НС по обучающей выборке можно записать в виде:
То есть, весовые
коэффициенты
Наверное,
некоторые из вас уже догадались, что точка минимума функционала
где Расписывая функционал качества, получим:
Или, учитывая, что:
имеем:
Это общий вид
градиентного алгоритма для нахождения весовых коэффициентов
не подходит для реализации градиентного алгоритма обучения. Кроме того, ее производные до порогового значения и после него равны нулю и из-за этого градиентный алгоритм не сможет менять веса связей. Какие же функции выбрать? На сегодняшний день, одной из наиболее распространенных функций активаций для скрытых слоев, является функция вида (ReLU):
На заре нейронных сетей, в основном, применялись:
А на выходном слое часто используют следующие:
Конечно, функций активации огромное множество. С некоторыми из них мы с вами будем знакомиться по мере прохождения этого курса. Итак, чтобы
выполнить обучение НС с помощью градиентного алгоритма необходимо выбрать
дифференцируемые функции активации и дифференцируемую функцию потерь, на основе
которой определяются рассогласования между текущим выходным значением НС Курс по нейронным сетям: https://stepik.org/a/227582 Видео по теме |
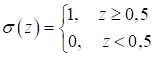
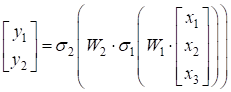
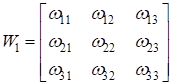 -
матрица весов связей скрытого слоя;
-
матрица весов связей скрытого слоя;
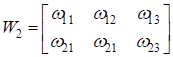 -
матрица весов связей выходного слоя.
-
матрица весов связей выходного слоя.
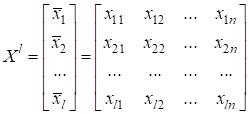
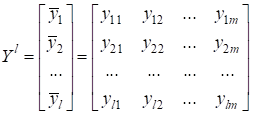
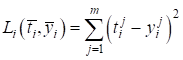
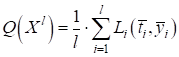
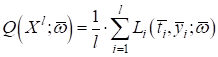
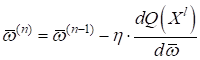
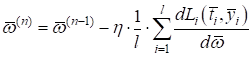
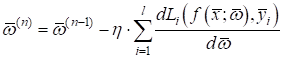
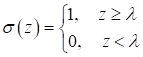
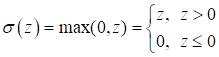
 -
функция softmax для задач M-классовой
классификации.
-
функция softmax для задач M-классовой
классификации.




















































