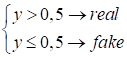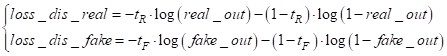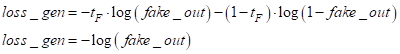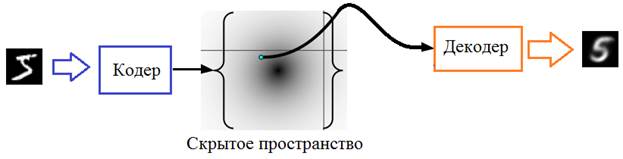
|
Генеративно-состязательные сети (GAN)Рассмотренный на предыдущем занятии вариационный автоэнкодер был способен формировать компактное скрытое пространство и генерировать на его основе выходной сигнал, в частности, изображения цифр. И для решения этой задачи мы задавали два критерия: дивергенция Кульбака-Лейблера (для формирования желаемой формы ПРВ точек скрытого пространства) и квадрат рассогласования между входным и выходным изображениями. Именно этот второй критерий «заставлял» декодер восстанавливать сигнал близкий к входному:
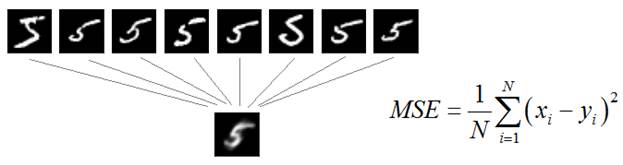
Однако изображения на выходе получались смазанными. Почему так происходит? Дело в том, что любая НС в процессе обучения старается уловить, сформировать закономерности между входными и выходными данными так, чтобы минимизировать заданный критерий. Теперь представьте, что у нас есть множество похожих пятерок и декодер для них должен сформировать адекватный ответ:
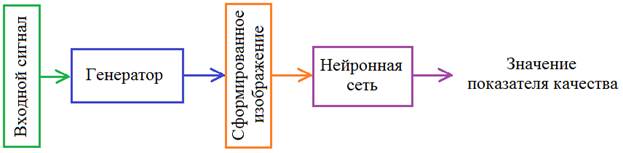
Именно такая сглаженная пятерка будет удовлетворять минимуму среднего квадрата ошибки рассогласования между всеми этими входами. Но, в данном случае, результат не совсем такой, какой бы мы хотели. Было бы куда лучше иметь нормальное, четкое изображение цифры, пусть даже с бОльшим значением показателя MSE. Визуально это воспринималось бы естественнее. Тогда, может быть, взять какой-то другой критерий для формирования четких цифр? К сожалению, таких чисто математических формул не существует. Все они будут, так или иначе, приводить к усреднению или выделению какого-то одного наблюдения. Как же тогда решить эту задачу? В 2014-м году Ян Гудфеллоу (Ian Goodfellow) предложил новую концепцию, известную сейчас под названием генеративно-состязательные сети (Generative Adversarial Networks). Ключевая идея заключается в формировании критерия качества для генератора с помощью еще одной НС:
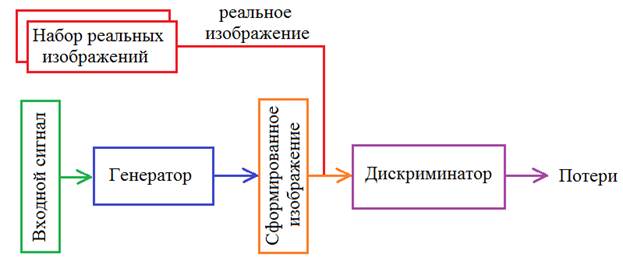
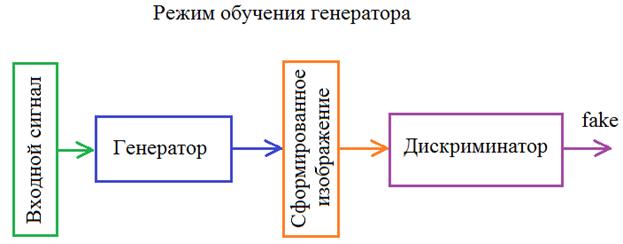
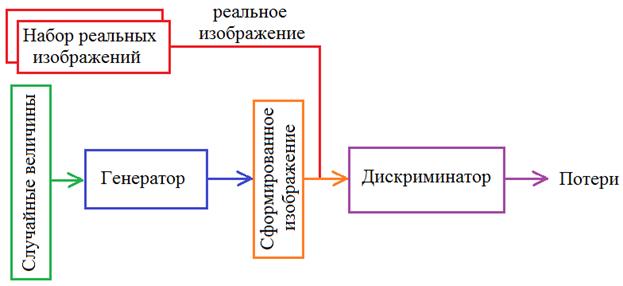
И здесь возникает вопрос: как выбрать показатель качества для генерации реалистичных изображений? Ян Гудфеллоу предложил оригинальное решение. Давайте подавать на вход второй НС и сгенерированные и реальные изображения, а она должна будет отличать первых от вторых. Такая сеть получила название дискриминатор:
На выходе
дискриминатора формируется одно числовое значение
То есть, на вход дискриминатора сначала можно подать реальное изображение, получить значение на выходе (назовем его real_out), а потом подать сгенерированное и вычислить другое значение (fake_out). Затем, используя эти выходные значения, вычислить потери по формуле бинарной кросс-энтропии (так как решается задача бинарной классификации на реальные и фейковые изображения):
где
Из этой формулы итогового показателя качества для дискриминатора видно, что потери должны быть минимальны для реальных изображений и максимальны для сгенерированных. В свою очередь генератор должен так построить изображение, чтобы дискриминатор не смог отличить его от реального:
Значит, в режиме
обучения генератора в бинарной кросс-энтропии требуемый отклик
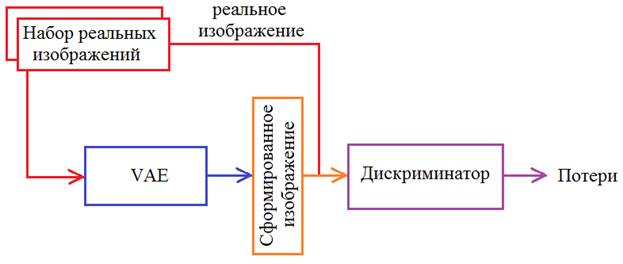
Получается, что дискриминатор и генератор конкурируют друг с другом и обучаются так, чтобы дискриминатор понимал входы от генератора, а генератор, наоборот, пытается «замаскировать» свою деятельность под реальные изображения. В результате такой конкуренции дискриминатор все лучше и лучше отличает реальные от фейковых изображений, а генератор все точнее и точнее создает реалистичные изображения. В идеале генератор должен формировать изображения неотличимые от реальных так, чтобы дискриминатор уже не мог их различать. Это пример того, как взаимная конкуренция приводит к развитию обеих нейронных сетей. Отсюда и пошло название «генеративно-состязательные». Я думаю идея, предложенная Яном Гудфеллоу, в целом, понятна. Берутся наборы реальных изображений близких к тем, что должен выдавать генератор. Затем, на вход дискриминатора подается случайно выбранное реальное изображение и вычисляется значение real_out. Затем, подается сгенерированное и вычисляется значение fake_out. В соответствии с функцией потерь loss_dis (дискриминатора) обучаем его алгоритмом обратного распространения ошибки. На следующем шаге подаем на вход дискриминатора сгенерированное изображение и по значению fake_out выполняем обучение уже генератора. Так, поочередно, обучая то одну, то другую сеть, мы их улучшаем в соответствии с выделенными критериями (функциями потерь). Возможно, у вас остается вопрос: что подавать на вход генератора? Как вариант, можно взять вариационный автоэнкодер из предыдущего занятия и выполнять его обучение, чтобы он генерировал реалистичные изображения, а не смазанные. Схема этой сети будет выглядеть так:
Но мы на следующем занятии реализуем другую идею. От вариационного автоэнкодера оставим только декодер (назовем его генератор), и на его вход будем подавать просто случайные величины, распределенные по нормальному закону с нулевым МО и единичной дисперсией:
В результате генератор сформирует компактное пространство гауссовского распределения, из которого можно будет выбирать произвольную точку и по ней формировать с помощью генератора то или иное изображение. Примеры использования GANЯ думаю, вы уже знаете, на что способны современные генеративные сети? Они применяются для самых разных задач. В самом простом случае, это может быть масштабирование изображений:
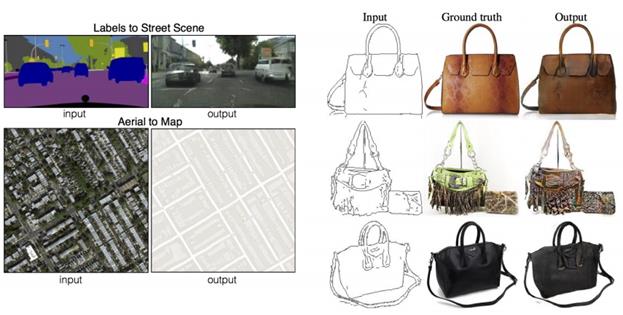
(взято из: Ledig, C., Theis, L., Huszar, F., Caballero, J., Aitken, A. P., Tejani, A., Totz, J., Wang, Z., and Shi, W. (2016). Photo-realistic single image super-resolution using a generative adversarial network.) Или формирование реалистичных изображений по наброску или, наоборот, построение схемы карты по спутниковому изображению:
(взято из: Isola, P., Zhu, J.-Y., Zhou, T., and Efros, A. A. (2016). Image-to-image translation with conditional adversarial networks.) А сочетание идеи эмбеддинга изображений и их генерации позволяет реализовывать интересные эффекты, когда, например, берется embedding-вектор мужского лица с очками, из него вычитается вектор мужского лица без очков и складывается с вектором женского лица. По результирующему embedding-вектору генератор способен сформировать различные женские лица в очках:
(взято из: Radford, A., Metz, L., and Chintala, S. (2015). Unsupervised representation learning with deep convolutional generative adversarial networks.) И это только небольшая часть простых примеров использования GAN. Область их применения, фактически, ограничивается только нашей фантазией. И сейчас они используются повсеместно от создания фрагментов в художественных фильмах до, известных всем, deep-fake’ов. Видео по теме |
.
Допустим, к выходу применяется сигмоидальная функция и тогда диапазон выходных
значений будет [0; 1]. Эти числа можно воспринимать как степень уверенности
дискриминатора в том, что изображение реальное или фейковое. В частности, если:
- целевое
значение для реальных изображений; 
- целевое
значение для фейковых изображений. Упрощая и суммируя эти потери, получаем:
.
Получаем критерий качества:
