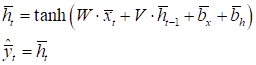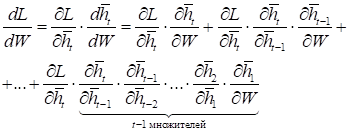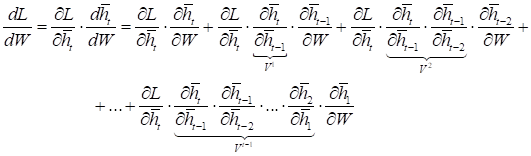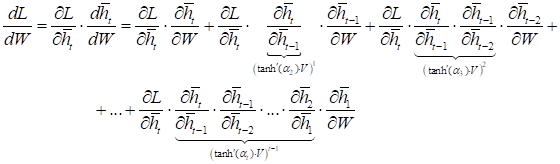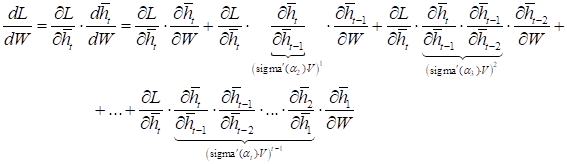|
Функции активации в RNN. Двунаправленные (bidirectional) RNN-слоиВ программах наших занятий мы в рекуррентном слое использовали функцию активации tanh – гиперболический тангенс. И это довольно частый выбор. Однако когда рассматривали полносвязные и сверточные нейронные сети, то там рекомендовалось применять другую функцию активации – ReLU. Возникает вопрос, почему в рекуррентных слоях мы не следуем этому правилу сетей прямого распространения? Давайте разберемся.
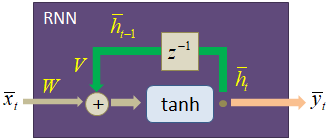
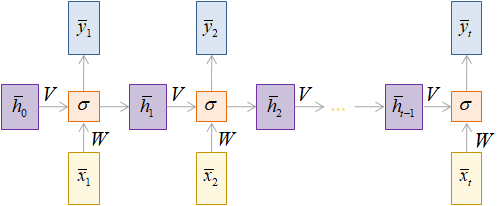
Как мы уже знаем, любой рекуррентный слой можно развернуть во времени и представить в виде следующего графа вычислений:
Также мы знаем, что на каждой итерации выходное значение вектора скрытого состояния вычисляется по формуле:
Теперь, если формально расписать порядок вычисления производной для некоторой выбранной функции потерь:
по матрице весовых коэффициентов W, получим выражение:
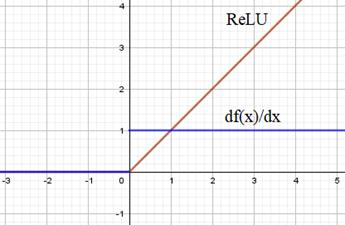
Что из него следует? Смотрите, если выбрать в качестве функции активации ReLU:
То ее
производная будет либо 0, либо 1. Пусть, для простоты, производная от ReLU у нас всюду
получается равной 1. Тогда в формуле вычисления производной от функции потерь в
слагаемых появляется умножение на матрицу V в степени
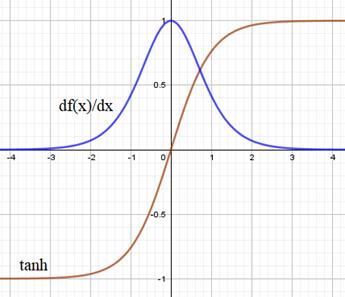
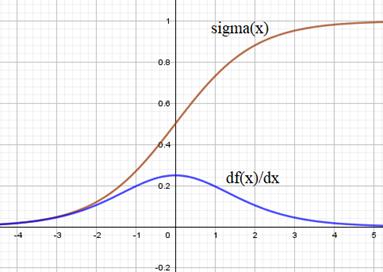
Отсюда хорошо видно, что если определитель матрицы V больше единицы, то она приведет к экспоненциальному росту слагаемых и, как следствие, общего градиента по функции потерь. Если же определитель меньше единицы, то получаем обратный эффект затухания градиентов. Причем экспоненциальный рост в функции ReLU сверху ничем не ограничен. Здесь могут получаться просто гигантские значения. Хорошо, давайте теперь посмотрим, чем гиперболический тангенс будет качественно отличаться от ReLU. Его график вместе с производной выглядит следующим образом:
А производная функции потерь будет содержать такие слагаемые:
Благодаря тому, что производная от гиперболического тангенса практически всюду меньше единицы, то она с большой вероятностью будет уменьшать значения матрицы V и, как следствие, риск взрыва градиентов существенно уменьшается. Теперь они, в основном, будут только затухать. Ну а что насчет сигмоидной функции активации:
Производная функции потерь будет иметь вид:
А график производной сигмоиды следующим образом:
Из рисунка видно, что производная сигмоиды напоминает производную гиперболического тангенса, но с куда меньшим масштабом: все значения много меньше единицы. Это значит, что такая функция потерь в рекуррентных слоях значительно быстрее будет устремлять градиенты к нулю, чем гиперболический тангенс. По этой причине предпочтение отдается гиперболическому тангенсу среди всех широко распространенных функций активаций. Также обратите
внимание, что слагаемые с большим числом множителей в производной функции
потерь относятся к начальным входным данным. А чем ближе к концу, тем
множителей все меньше. Это приводит к тому, что в итоговом градиенте, в
основном, учитываются последние входные данные, и в меньшей степени –
начальные. То есть, рекуррентный слой в большей степени обучается на последних
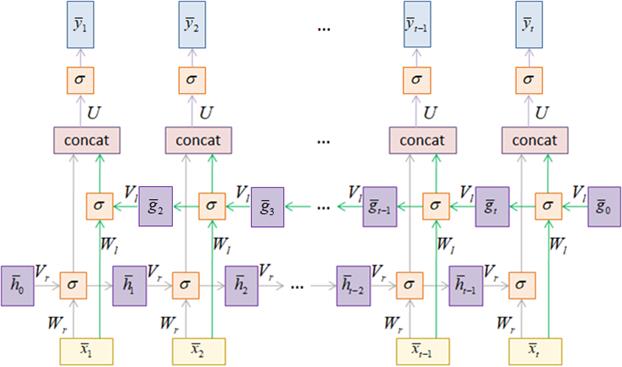
данных и, как результат, вектор скрытого состояния Как бороться со взрывом градиентов, мы с вами уже говорили. Хорошей эвристикой здесь является ограничение их величины некоторым пороговым уровнем. А вот побороть их быстрое затухание, задача куда сложнее. Для ее решения были предложены более сложные схемы рекуррентных слоев LSTM и GRU, о которых мы еще будем говорить. Двунаправленные рекуррентные сетиНо есть еще один подход, позволяющий учесть больше информации в векторе скрытого состояния даже при использовании простого элмановского рекуррентного слоя. Что это за подход? Смотрите, не редко бывают задачи, когда известна вся последовательность целиком и ее нужно обработать. Например, разделить короткие фразы по семантической окраске: негативное или позитивное высказывание. Или же понять гендерную принадлежность фразы: мужская, женская. И так далее. Что дает нам наличие всех элементов обрабатываемой последовательности? Очевидно то, что можно сначала пройти по всем ее элементам в одном (прямом) направлении, а затем, в обратном, формируя два вектора скрытого состояния. И уже на основе этих двух векторов вычислять выходные значения. Приходим к идее двунаправленных рекуррентных слоев.
На рисунке
представлена развертка такого слоя во времени. Выглядит масштабно, но на самом
деле все предельно просто. Сначала выполняется стандартный прямой проход по
элементам последовательности с рекуррентным вычислением векторов
с начальным
значением Далее делается все то же самое, но при движении от последнего элемента последовательности до первого с вычислением других векторов скрытого состояния на каждой итерации:
с начальным
значением При движении в обратном направлении можно сразу вычислять соответствующие выходные значения. Для этого векторы скрытых состояний двух разных уровней объединяются между собой в один общий вектор:
А затем, он пропускается через полносвязный слой, формируя итоговое выходное значение для текущего шага рекурсии:
В результате такой обработки сеть имеет возможность лучше учитывать, как самые первые, так и последние элементы последовательности, а значит, результат прогноза вполне может улучшиться. Конечно, расплачиваться за такую двунаправленную обработку приходится заметно большим числом настраиваемых параметров и более длительным временем обучения, т.к. нужно пройтись по каждой последовательности дважды. Однако, в ряде случаев, двунаправленные рекуррентные слои могут заметно улучшить качество работы модели. Видео по теме |
на
каждом k-м рекуррентном
шаге:
будет
ориентирован в большей степени на них, быстро «забывая» начальные входные
значения. По этой причине вектор 
по
уже знакомой нам формуле:
.
Здесь индекс r у матриц и
смещений означает как бы движение вправо (прямой ход). При этом сохраняются все
вычисленные векторы скрытого состояния 
.
.
Здесь используются свои матрицы преобразований 
и
смещения 
.
