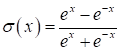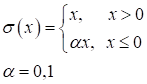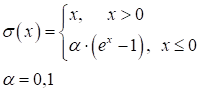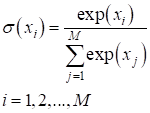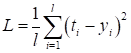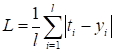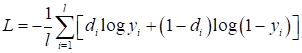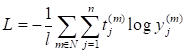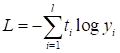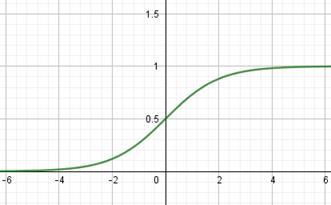
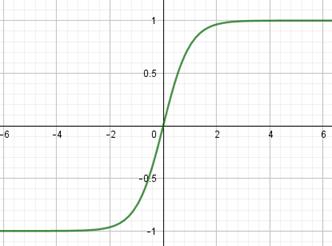
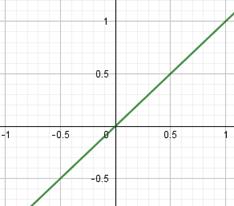
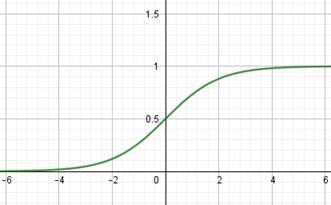
|
Функции активации и потерь в PyTorchТеперь, когда мы в целом познакомились с идеей НС и алгоритмом их обучения back propagation, пришло время подробнее рассмотреть различные функции активации и потерь, которые имеются в PyTroch. Начнем с функций активаций нейронов. Набор наиболее используемых функций доступен в ветке: torch.nn.functional Обычно она импортируется следующим образом: import torch.nn.functional as F И затем идет выбор той или иной функции активации через короткий псевдоним F. Одними из первых стали применять функции сигмоиды и гиперболического тангенса:
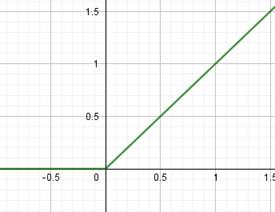
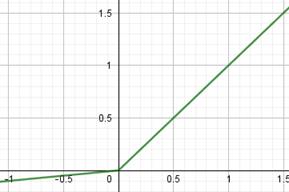
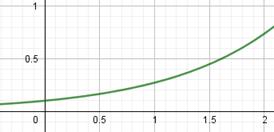
Они очень похожи между собой с одним кардинальным различием, что сигмоида отображает выходные значения в диапазон [0; 1], а гиперболический тангенс – в диапазон [-1; 1]. Сейчас их применяют либо в сетях с небольшим числом слоев (2-3 слоя), либо в нейронах выходного слоя. Глубокие НС (с числом слоев от 10 и более) с такими функциями обучаются крайне сложно. Это связано с наличием у них практически пологих участков (областей насыщения), где производные близки к нулю. И, как следствие, алгоритм back propagation с такими производными практически не изменяет веса связей, а значит и не обучает НС в целом. Последнее время для нейронов скрытых слоев стали применять следующие функции активации:
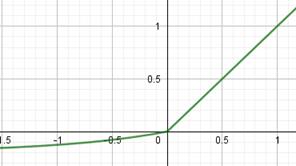
Из них самая используемая – это ReLU (Rectified Linear Unit). Особенность всех этих трех функций в том, что они не имеют пологих участков в положительной области. Благодаря этому производные не обнуляются и процесс обучения глубоких НС протекает гораздо быстрее. Конечно, глядя на график функции ReLU, возникает вопрос в наличии пологого участка, где производная равна нулю. Разве он не сказывается негативно на процессе обучения? Как показала практика, нет, т.к. входная сумма на каждом нейроне может произвольно увеличиваться или уменьшаться на величину bias и тем самым выводить общую сумму из пологой области. Поэтому такая простая и незамысловатая функция оказалась крайне эффективной при обучении и последующей работе глубоких НС. Две другие функции все же имеют некоторый наклон в отрицательной области, как раз для избегания нулевых значений производных. Но это не часто дает заметный прирост скорости и точности обучения НС, а потому они реже используются на практике. На выходном слое НС применяются разные функции активации в зависимости от решаемых задач:
Функция linear обычно используется в задачах регрессии, когда выходное значение на нейроне никак не нужно изменять. Надо сказать, что эту функцию активации имеет смысл применять только на нейронах выходного слоя, так как нейрон становится линейным. А композиция линейных моделей (нейронов) может быть описана одной эквивалентной моделью. Поэтому все скрытые слои НС с такой функцией активации могут быть заменены одним единственным нейроном. Как вы понимаете, такая НС мало на что пригодна. Сигмоидная функция активации часто применяется для формирования выходного значения в задачах бинарной классификации. Ее значения [0; 1] могут быть интерпретированы, как «уверенность» сети в том или ином прогнозе. Последняя функция активации SoftMax применяется в задачах многоклассовой классификации. Она тоже для каждого выхода дает значения в диапазоне [0; 1], а сумма всех выходов всегда равна 1. То есть, их можно интерпретировать в некотором смысле, как вероятности определения того или иного класса. Конечно, функций активаций куда больше рассмотренных, но этих будет вполне достаточно для первого опыта построения и обучения самых разных архитектур НС. Функции потерьКак мы с вами уже знаем, при обучении НС алгоритмом back propagation необходимо определять качество работы сети в целом. Делается это с помощью выбора подходящей функции потерь. Но, что значит «подходящая»? Это определяется с позиции здравого смысла и опыта разработчика. Например, в задачах регрессии чаще всего применяют функцию минимума среднего квадрата ошибки между заданными (целевыми) значениями и теми, что выдает НС:
где В PyTorch функции потерь реализованы в виде классов и располагаются в ветке: torch.nn В частности квадратическая функция представлена классом: nn.MSELoss Это сокращение от Mean Squared Error Loss (средняя квадратичная ошибка). В таблице ниже представлены основные функции потерь с их аналитическими выражениями.
Конечно, это не все возможные функции потерь, но для начала вполне достаточно приведенных. На следующих занятиях мы будем использовать некоторые из рассмотренных функций, и вы сможете познакомиться с ними подробнее. Видео по теме |
- целевые
значения для каждого i-го входного образа (вектора) обучающей
выборки; 
- реальный
отклик сети, при предъявлении i-го образа; 
- размер
обучающей выборки.
