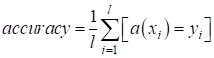Форматы представления выборок. Сбалансированность и репрезентативность

Смотреть материал на YouTube | RuTube

До сих пор мы с вами в программах использовали очень маленькие выборки. Но, как вы понимаете, на практике часто они куда больше и объемнее. Обычное дело, когда в обучающей выборке содержатся от десятков тысяч до миллионов различных образов. Эти данные нужно уметь правильно хранить и загружать в память при обучении и тестировании нейронных сетей.

Если образы выборки представлены числовыми и категориальными признаками, то часто они хранятся в одном или нескольких текстовых файлах, например, в формате csv или json. Или же в таблицах базы данных. Вот один пример такой выборки, взятой с известного сайта kaggle:

https://www.kaggle.com/datasets/janiobachmann/bank-marketing-dataset

age	job	marital	education	default	balance	housing	loan	...	deposit
59	admin.	married	secondary	no	2343	yes	no	...	yes
56	admin.	married	secondary	no	45	no	no	...	yes
60	retired	divorced	secondary	no	545	yes	no	...	yes
...								...	...
43	admin.	single	secondary	no	35	no	no	...	no
60	retired	divorced	tertiary	no	-134	no	no	...	no

Каждый образ этой выборки состоит из 16-ти признаков, а последний столбец описывает целевые значения: yes или no (есть депозит или нет). Это соответствует задаче бинарной классификации. Если бы решалась задача регрессии, то целевые значения содержали бы требуемые числовые значения. Причем таких столбцов может быть больше одного. Например, при решении задач определения местоположения нейронная сеть на выходе может выдавать координаты на плоскости (x, y) или в пространстве (x, y, z) и так далее. То есть, в подобных таблицах важно знать, какие столбцы описывают признаки образов, а какие относятся к целевым значениям. Обычно эта информация указывается в описании к выборке.

Общий размер таких данных редко достигает десятков или сотен мегабайт. Поэтому их можно целиком загружать в память и хранить в тензорах фреймворка PyTorch. А, затем, подавать на вход нейронной сети для ее обучения или тестирования.

Однако не редко на практике выборка может занимать десятки, а то и сотни гигабайт. Например, в известном конкурсе ImageNet классификации полноцветных изображений выборка состоит из десятка миллионов изображений и занимает гигабайты. Понятно, что хранить всю ее в памяти было бы нецелесообразно. И здесь возникает задача правильной организации таких объемных данных с последующей их загрузкой в память устройства.

Так как изображения это частый случай набора данных для обучения нейронных сетей, то профессиональное сообщество выработало схему их хранения на внешних носителях.

Создается общая папка (пусть она называется dataset) с двумя подкаталогами:

train – набор изображений для обучения;
test – набор изображений для тестирования.

Внутри этих подкаталогов изображения разбиты на классы с помощью вложенных папок: class_1, class_2, … Конечно, названия каталогов могут быть и другими, но их структура в целом имеет такой вид. Дополнительно в корневой папке dataset может располагаться файл, как правило, или в формате json или csv, который соотносит каждый каталог class_1, class_2, … с соответствующей меткой класса. Например:

{
    "class_1": 1
    "class_2": 2
    "class_3": 3
    "class_4": 4
     …
}

Если же такого файла нет, то часто полагается, что метки классов можно выделить из самих названий папок. В нашем примере последняя цифра подкаталогов, как раз отвечает за номер класса.

Конечно, это не единственно возможная структура организации хранения изображений выборок. Давайте представим, что нам нужно находить координаты центра солнца на изображении. Получаем задачу регрессии, когда нейронная сеть на входе получает изображение, а на выходе дает координаты (x, y) центра солнечного диска. В этом случае можно сформировать два подкаталога train и test и в каждом разместить файлы изображений с разным расположением солнца на разных фонах:

А координаты солнца для каждого изображения сохранить в файле format.json:
{
    "sun_reg_1.png": [113, 131],
    "sun_reg_2.png": [123, 185],
    …
}

Для других типов задач, использующих изображения в качестве входных данных, структура каталогов может меняться. Главное, чтобы ее впоследствии можно было легко расширять (добавлять новые образы) и взаимодействовать на программном уровне.

Сбалансированность и репрезентативность выборок

Следующий важный вопрос – это качество выборки. Очевидно, что когда решается задача классификации, то количество образов каждого класса должно быть примерно одинаковым. Это касается и обучающей и тестовой выборок. То есть, выборки должны быть сбалансированными. Почему это так важно? Рассмотрим радикальный пример, когда много образов первого класса и много меньше образов других классов. Тогда нейронной сети достаточно всегда выдавать прогноз самого многочисленного (первого) класса:

чтобы обеспечить высокое значение показателя правильной классификации:

То есть, с такой сильно несбалансированной выборкой алгоритмы классификации (обученные по ней) будут отдавать предпочтение образам первого класса, практически игнорируя остальные.

Но одного равного количества образов классов недостаточно. Еще важно разнообразие примеров в пределах каждого класса. Например, вот так выглядят наборы изображений цифр известного датасета MNIST:

Здесь видим самые разные начертания цифр от 0 до 9. Благодаря этому нейронная сеть получает возможность построить обобщенное представление для каждой цифры. И в последующем (при эксплуатации) будет способна улавливать самые разные вариации изображения цифр, усвоенные из этой обучающей выборки. Такое разнообразие образов каждого класса называется репрезентативностью.

Если бы в выборке содержались примерно одинаковые изображения какой-либо цифры, например, нуля:

то обученный алгоритм, скорее всего, с ошибками обработал бы сильно отличающиеся изображения вида:

и, возможно, отнес бы их к другому классу. Для минимизации таких ошибок необходимо максимальное разнообразие образов каждого класса. То есть, выборка должна быть репрезентативна. В результате получаем два главных свойства для выборок: по возможности они должны быть сбалансированными и репрезентативными.

Форматы представления выборок. Сбалансированность и репрезентативность

Сбалансированность и репрезентативность выборок

Видео по теме