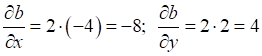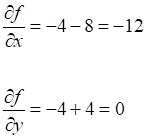|
Автоматическое дифференцированиеКурс по нейронным сетям: https://stepik.org/a/227582 Ранее мы с вами
с нуля реализовали алгоритм back propagation для очень
простой НС. И увидели, что в его основе лежит вычисление производной от
выбранной функции потерь по вектору параметров
которая зависит
от функции Автоматическое дифференцированиеДавайте представим, что у нас есть функция вида:
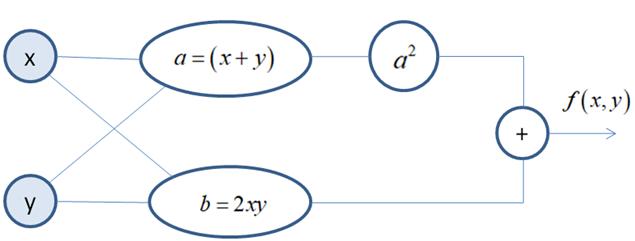
и мы хотим посчитать ее значения при разных x, y. Один из способов сделать это – построить граф вычислений следующим образом:
Эффективность здесь достигается за счет устранения дублирования при вычислениях (если они возникают), а также за счет распараллеливания независимых операций. Кроме того, как мы сейчас увидим, такой граф также позволяет эффективно вычислять и производные функции, что весьма полезно при разработке алгоритмов машинного обучения и, вообще, при решении различных оптимизационных задач. Общая идея вычислительного графа – представить целевую функцию набором элементарных математических операций (сложение, вычитание, умножение, деление) и стандартного набора функций (sin, cos, exp, log, sqrt и т.д.). Существует теорема, доказывающая, что любую непрерывную функцию можно представить с заданной точностью набором таких математических действий, то есть, с помощью вычислительного графа. Давайте теперь посмотрим, как эта конструкция позволяет вычислять производные. Воспользуемся вычислительным графом для функции:
и рассмотрим идею нахождения производных, которая реализована в PyTorch. Сразу отмечу, что мы будем искать численные значения производных, а не их аналитический вид. То есть, PyTorch выполняет численное дифференцирование функций, используя для этого метод обратного вычисления производных (reverse mode differentiation), известный также под названием автоматическое дифференцирование: https://en.wikipedia.org/wiki/Automatic_differentiation Это значит, что вначале нам нужно переменным x, y присвоить некоторые значения, для которых будут вычисляться частные производные. Пусть, x = 2, y = -4. Пропускаем эти значения по графу и запоминаем результаты вычислений в каждом узле. Затем PyTorch приступает к
вычислению частных производных сложной функции
где
Фактически, это правило вычисления производной сложной функции, известное еще со школьной скамьи. Чтобы было понятнее, применяя его, получим следующие значения частных производных в аналитическом виде:
Но вернемся к PyTorch. Процесс
вычисления производных начинается с конца (истока), то есть, вычисляется
производная
Так как
функциональные узлы вычислительного графа составлены из элементарных функций,
то PyTorch «знает»
аналитический вид их производных. И, в частности, «понимает», что
Далее, по цепному правилу нам нужно вычислить частную производную
Она просто равна
1, поэтому Следующим шагом нам нужно вычислить производную:
И, затем, на
основе частных производных
Складываем полученные величины и находим частные производные функции по x и y:
Вот так, с
помощью вычислительного графа, мы определили значения производных функции Реализация автоматического дифференцирования на PyTorchЧтобы увидеть, как вся эта математика реализуется на PyTorch, выполним вычисления производных этой же функции в той же точке x = 2, y = -4. Для этого я приведу следующую простую программу: import torch x = torch.tensor([2.0], requires_grad=True) y = torch.tensor([-4.0], requires_grad=True) f = (x + y) ** 2 + 2 * x * y f.backward() print(f) print(x.data, x.grad) print(y.data, y.grad) Давайте детально
разберемся, как она работает. Вначале объявляются два тензора x и y с вещественными
значениями 2 и -4. Причем, у тензоров дополнительно указан аргумент requires_grad=True, который
«указывает» фреймворку PyTorch вычислять для них градиенты. По
умолчанию этот параметр равен False: requires_grad=False. После этого
вычисляется значение функции
Причем, программа будет корректно работать, даже если формулу расписать в несколько строчек с промежуточными переменными, например: a = (x + y) ** 2 b = 2 * x * y f = a + b f.backward() Как же это происходит? На самом деле очень просто. Тензоры x и y в PyTorch – это не просто наборы чисел и операций с ними, а программные единицы, которые неявно взаимодействуют между собой. В частности, команды: a = (x + y) ** 2 b = 2 * x * y f = a + b не только вычисляют итоговое значение f, но и формируют (неявно) граф вычислений, начиная с начальных значений тензоров x, y. Поэтому метод backward всегда имеет возможность вычислить численные значения производных для функции f. Курс по нейронным сетям: https://stepik.org/a/227582 Видео по теме |
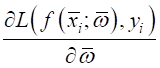
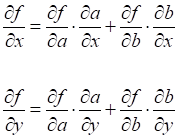
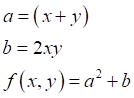
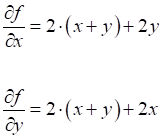
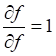 (которая,
очевидно, равна 1). Далее, в соответствии с цепным правилом, нам нужно
вычислить производную:
(которая,
очевидно, равна 1). Далее, в соответствии с цепным правилом, нам нужно
вычислить производную:
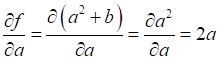
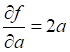 .
Само значение
.
Само значение 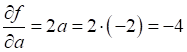
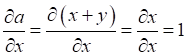
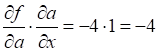 .
Аналогично сразу вычисляем и производную
.
Аналогично сразу вычисляем и производную 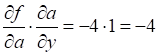 .
.
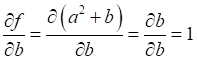
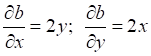 вычислить
их при x = 2, y = -4:
вычислить
их при x = 2, y = -4: