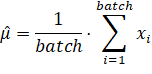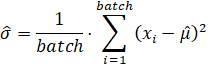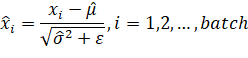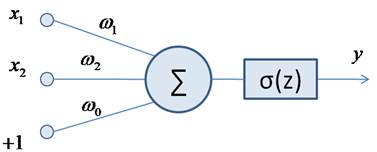
Алгоритм Batch Normalization

Смотреть материал на YouTube | RuTube

В 2015-м году два американских исследователя Сергей Иоффе (Sergey Ioffe) и Кристиан Сегеди (Christian Szegedy) опубликовали статью, в которой предложили алгоритм ускорения обучения глубоких НС под названием Batch Normalization. Идея оказалась настолько удачной, что теперь повсеместно используется в самых разнообразных архитектурах НС. Что же они предложили?

Еще на заре становления НС ученые заметили значительные изменения статистики выходного сигнала нейрона даже при небольших изменениях весов связей. Например, если взять простейшую НС с двумя входами x1, x2 и одним нейроном с функцией активации ReLU:

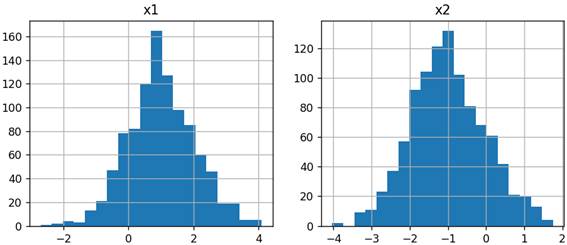
то при подаче на вход случайных значений, распределенных по нормальному закону:

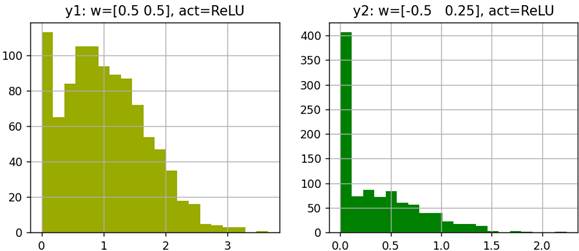
на выходе нейрона при весах связей w1 = 0.5, w2 = 0.5 и w0 = 1.0, получим распределение вида:

А при весах связей w1 = -0.5, w2 = 0.25, w0 = 1.0 распределение (гистограмма) резко меняет свою форму. И это не удивительно, т.к. большая часть значений оказывается в отрицательной области, где функция ReLU их обнуляет. Поэтому мы видим большой нулевой столбец и небольшое количество остаточного сигнала в положительной области. Картина кардинально не меняется и при других нелинейных функциях активации. В результате можно заключить, что даже небольшие изменения весов связей, подходящих к нейрону, могут заметно менять распределение его выходных значений.

Ну хорошо, эффект такой мы видим. Но почему это вызывает какие-либо озабоченности и проблемы? Если бы у нас был всего один скрытый слой нейронов, то на все это можно было бы закрыть глаза.

Но при большом их числе постоянное значимое изменение распределений на выходах нейронов, как бы, «сбивает» текущие настройки нейронов следующего слоя. Они только, только обучились на одно распределение входного сигнала, а следом идет уже совсем другое, и нужно практически полностью переучиваться (подстраивать веса связей под новое распределение). В результате обучение НС в целом затрудняется и замедляется. В этом главный негативный эффект постоянного и радикального видоизменения распределений на выходах нейронов.

Но что мы можем с этим сделать? Первой мыслью было выполнить просто нормировку в пределах каждого батча на выходах каждого нейрона так, чтобы среднее значение сигнала было равно нулю, а дисперсия единице. То есть, на каждом выходе нейронов сначала вычисляется среднее и диспресия по батчу:

А затем, выполняется нормировка этого батча (пакета) по формуле:

Здесь - небольшая положительная добавка, чтобы избежать деление на ноль при нулевом значении . Такая процедура выполняется независимо на выходах каждого нейрона текущего слоя.

Но, этого недостаточно. Если нормировку оставить в таком виде, то нейроны теряют смещение (bias), так как среднее по каждому пакету всюду равно нулю. Да и строго единичная дисперсия тоже вызывает вопросы. Поэтому Иоффе и Сегеди предложили нормированные значения дополнительно умножать на некоторое число гамма и смещать на величину бета:

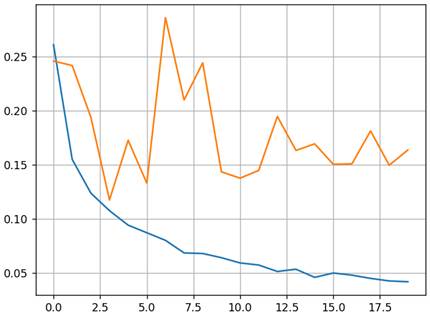
Причем параметры следует также подбирать с помощью алгоритма back propagation. То есть, в нейронной сети появляются дополнительные настраиваемые параметры. В результате для слоя, где применяется алгоритм Batch Normalization стандартные bias (байесы) теряют свой смысл и их лучше отключать, чтобы не добавлять лишние, по сути, не используемые параметры сети. Роль смещений теперь будут играть параметры слоя Batch Normalization.

Реализация Batch Normalization на PyTorch

Вот основная идея алгоритма Batch Normalization. Давайте посмотрим, как можно его реализовать во фреймворке PyTorch на примере все той же НС классификации изображений цифр.

В классе модели DigitNN достаточно создать слой Batch Normalization с помощью класса BatchNorm1d, указав размерность входного сигнала (по сути, число нейронов слоя, к которому будет применен Batch Normalization). А затем, в методе forward после функции активации скрытого слоя применить объект bm_1:

class DigitNN(nn.Module):
    def __init__(self, input_dim, num_hidden, output_dim):
        super().__init__()
        self.layer1 = nn.Linear(input_dim, num_hidden, bias=False)
        self.layer2 = nn.Linear(num_hidden, output_dim)
        self.bm_1 = nn.BatchNorm1d(num_hidden)
 
    def forward(self, x):
        x = self.layer1(x)
        x = nn.functional.relu(x)
        x = self.bm_1(x)
        x = self.layer2(x)
        return x

Обратите внимание, что в данной сети мы используем класс BatchNorm1d, который предполагает одномерный сигнал на выходах нейронов. Позже, когда мы будем рассматривать светочные НС, там выходной сигнал может быть двумерным и даже трехмерным. Соответственно для него следует использовать классы BatchNorm2d и BatchNorm3d. При этом принцип их работы сохраняется и аналогичен одномерному случаю.

Все, нормализацию по батчам мы добавили после первого слоя нейронов. Давайте посмотрим, к чему это приведет. После запуска программы и 20 эпох обучения модели (без L2-регуляризации):

model = DigitNN(28 * 28, 128, 10)

получим следующие графики потерь для тренировочной и валидационной выборок:

Видим, что сеть дошла до довольно низкого уровня потерь и при этом не наблюдается движения вверх графика валидации. А качество классификации на тестовой выборке составило рекордные для нашей сети 97%. Это говорит о том, что слой Batch Normalization не только способен ускорять и улучшать процесс обучения, но и снижает эффект переобучения сети. Ряд авторов отмечают, что алгоритм Batch Normalization работает на более фундаментальном уровне, чем алгоритм Dropout и в первую очередь следует применять нормировку пакетов, добиваясь приемлемого качества обучения НС® Самые ярые сторонники Batch Normalization утверждают, что от Dropout вообще следует отказаться, так как нормализация естественным образом приводит к обобщению работы нейронов и смысл в Dropout, как таковом, теряется. Так это или нет, сложно доказать, т.к. все это эвристики. Мало того, Batch Normalization, равно как и Dropout, не гарантирует улучшение обучения НС, а в ряде случаев и ухудшает ее работу. Поэтому вначале следует попробовать обучить модель без этих алгоритмов, и только по необходимости добавлять сначала Batch Normalization, потом отдельно Dropout и в самом крайнем случае комбинировать на разных слоях эти подходы. Причем Dropout не должен напрямую оказывать влияние на Batch Normalization, т.к. он искажает статистику из-за отключения части нейронов. По этой причине крайне не рекомендуется на одном и том же слое применять оба этих алгоритма.

Вот общие рекомендации применения различных инструментов борьбы с переобучением и ускорения обучения. Как их использовать в каждом конкретном случае, вам никто не скажет. Здесь в значительной степени играет роль опыт разработчика. А конечный вариант, как всегда, покажет только эксперимент.

Алгоритм Batch Normalization

Реализация Batch Normalization на PyTorch

Видео по теме