|
Алгоритм back propagation. Пример работыКурс по нейронным сетям: https://stepik.org/a/227582 Итак, наша
задача вычислить весовые коэффициенты
который мы с вами расписывали следующим образом:
Отсюда хорошо
видно, что конкретный вид градиента меняется в зависимости от выбранной функции
потерь
Набор из таких Но и это еще не
все. Современные НС часто содержат огромное количество параметров
где Математический вывод алгоритма обратного распространения ошибки при квадратической функции потерь я уже приводил в курсе по машинному обучению. Здесь же наглядно продемонстрирую принцип его работы на примере простой трехслойной НС.
Пусть начальные
веса связей выбираются случайным образом в диапазоне [-0.5; 0,5]. Верхний
индекс у весовых коэффициентов показывает их принадлежность к тому или иному
слою. Каждый нейрон имеет дифференцируемую функцию активации На первом шаге
делается прямой проход по сети. Пропускаем через нее вектор наблюдения
и последнее выходное значение d:
После этого вычисляется величина ошибки, как производная по функции потерь:
В частности, при квадратической функции потерь, имеем:
На данный момент все должно быть понятно. Мы много раз подробно рассматривали процесс распространения сигнала по НС, и вы это уже хорошо себе представляете. А вот дальше начинается самое главное – обратное распространение ошибки. Итак, у нас есть
ошибка
Используя вычисленный локальный градиент, пропускаем его обратно по весам связей и вычисляем ошибки для предыдущего слоя:
А затем, по аналогии, вычисляются следующие значения локальных градиентов:
Для первого скрытого слоя, снова выполняется пересчет ошибок:
и соответствующих локальных градиентов:
После этого выполняется корректировка весов связей в соответствии с градиентным алгоритмом, начиная с последнего (выходного) слоя и доходя до первого:
В результате, мы
выполнили одну итерацию алгоритма обучения НС. На следующей итерации следует
взять другой входной вектор из обучающего множества. Лучше всего это сделать
случайным образом, чтобы не формировались возможные ложные закономерности в
последовательности данных при обучении НС. Повторяя много раз этот процесс,
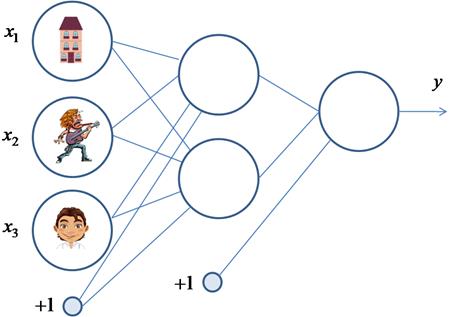
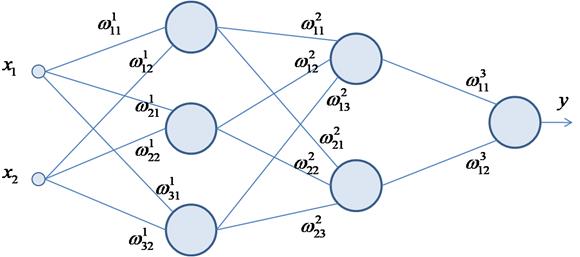
весовые коэффициенты Вот так, в целом выглядит идея работы алгоритма обучения по методу back propagation (обратного распространения ошибки). Давайте теперь в качестве примера обучим следующую НС:
В качестве обучающего множества выберем все возможные варианты (здесь 1 – это да, -1 – это нет):
На каждой итерации работы алгоритма, мы будем подавать случайно выбранный вектор и корректировать веса, чтобы приблизиться к значению требуемого отклика. В качестве функции активации выберем гиперболический тангенс:
со значением производной:
Пример реализации алгоритма back propagation на Python с использованием тензоров пакета PyTorch: neuro_net_12.py: https://github.com/selfedu-rus/neuro-pytorch/ Конечно, это довольно простой, примитивный пример, частный случай, когда можно обучить НС так, чтобы она вообще не выдавала никаких ошибок. Чаще всего в реальных задачах остается некоторый процент ошибок и наша задача сделать так, чтобы этих ошибок было как можно меньше. Курс по нейронным сетям: https://stepik.org/a/227582 Видео по теме |
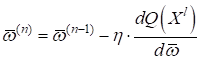
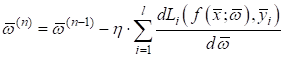
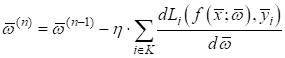
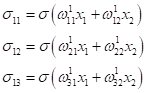
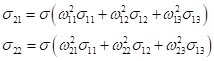
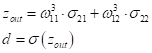
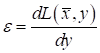
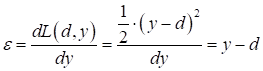
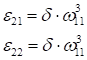
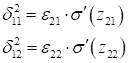
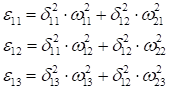
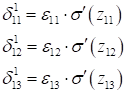
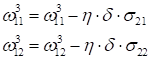
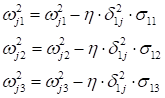 при
при
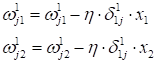 при
при