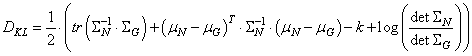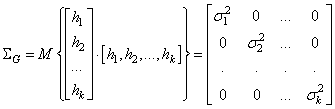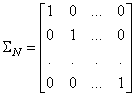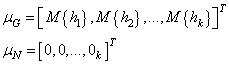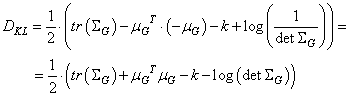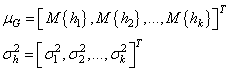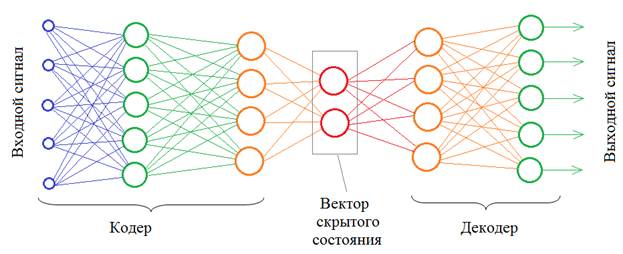
|
Вариационные автоэнкодеры (VAE). Что это такое?Курс по нейронным сетям: https://stepik.org/a/227582 На предыдущем занятии мы с вами познакомились с работой простого автоэнкодера, который воспроизводил изображения цифр по вектору скрытого состояния. Давайте теперь внимательнее посмотрим на область, которую формирует кодер при преобразовании таких изображений. Для этого воспользуемся простой полносвязной НС с двумя нейронами для описания вектора скрытого состояния:
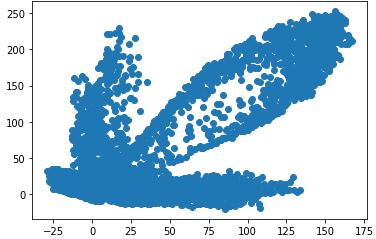
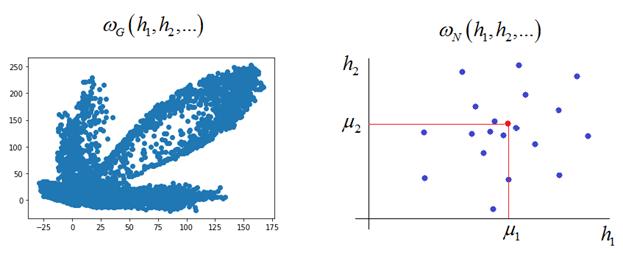
В пакете Keras мы отдельно опишем кодер и декодер и уже на их основе сформируем общий автоэнкодер: input_img = Input(shape=(28, 28, 1)) x = Flatten()(input_img) x = Dense(128, activation='relu')(x) x = Dense(64, activation='relu')(x) encoded = Dense(2, activation='linear')(x) input_enc = Input(shape=(2,)) d = Dense(64, activation='relu')(input_enc) d = Dense(28*28, activation='sigmoid')(d) decoded = Reshape((28, 28, 1))(d) encoder = keras.Model(input_img, encoded, name="encoder") decoder = keras.Model(input_enc, decoded, name="decoder") autoencoder = keras.Model(input_img, decoder(encoder(input_img)), name="autoencoder") autoencoder.compile(optimizer='adam', loss='mean_squared_error') Благодаря такой конструкции мы теперь можем обучить автоэнкодер в целом: autoencoder.fit(x_train, x_train, epochs=10, batch_size=64, shuffle=True) А, затем, отдельно использовать его кодер и декодер: h = encoder.predict(x_test) plt.scatter(h[:, 0], h[:, 1]) На графике увидим следующее распределение точек векторов скрытого состояния для тестового набора изображений:
Это характерная картина формирования модельной области отображения входного сигнала в пространство скрытого состояния. Что отсюда следует? Если мы будем брать точки в пределах сформированной области, то скорее всего, на выходе декодера будут получаться осмысленные изображения цифр. Если же брать точку за пределами этой области, то очень вероятно получим какое-то неопределенное изображение. Например, для точки с координатами
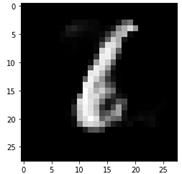
получим следующее изображение: img = decoder.predict(np.expand_dims([50, 250], axis=0)) plt.imshow(img.squeeze(), cmap='gray')
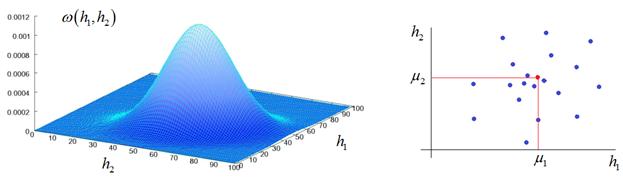
Напоминает шестерку, но выглядит не очень. Из-за этого автоэнкодеры в чистом виде не пригодны для генерации произвольных изображений. То есть, мы не можем брать произвольные точки в области скрытого состояния, чтобы гарантированно получать осмысленные изображения. Чтобы решить эту проблему пространство состояний скрытого вектора должно быть компактным и представлять единую цельную область без существенных разделений. Именно эту цель преследуют вариационные автоэнкодеры: Variational Autoencoders (VAE) Они пытаются сформировать область точек скрытого пространства в соответствии с заданным законом распределения. Часто выбирают нормальное (гауссовское) распределение, так как оно наиболее просто с вычислительной точки зрения, имеет понятную, приемлемую форму и полностью определяется двумя параметрами: математическое ожидание, дисперсия Например, в
случае двумерного вектора скрытого пространства
Такой подход даст нам уверенную надежду, что любая точка, взятая в пределах полученного распределения, будет давать на выходе декодера осмысленные, понятные изображения. То есть, мы будем понимать как выбирать точки в скрытом пространстве для генерации новых полноценных изображений. Это ключевое отличие вариационного автоэнкодера от обычных автоэнкодеров. Более того, эту же картину можно интерпретировать как преобразование входного пространства большей размерности в компактное скрытое пространство признаков меньшей размерности. Часто это упрощает дальнейший анализ исходных данных. Далее я приведу
теорию, необходимую для понимания построения вариационного автоэнкодера. Итак,
у нас есть формируемое и желаемое распределения точек скрытого пространства.
Обозначим их через
Задачей
алгоритма обучения будет не только точно воспроизвести входной сигнал, но и
распределить точки скрытого пространства как можно ближе к распределению дивергенция Кульбака-Лейблера (кому интересно, хороший материал по этой мере изложен на этой странице https://habr.com/ru/post/484756/). Так как мы предполагаем, что оба распределения будут гауссовскими с независимыми величинами вектора скрытого состояния
то расстояние Кульбака-Лейблера для этого случая записывается относительно просто, по следующей формуле:
Здесь
Здесь по главной диагонали стоят дисперсии соответствующих величин. Вторая ковариационная матрица желаемого распределения можно взять единичной:
Это будет означать, что многомерная гауссовская ПРВ будет иметь одинаковые дисперсии по всем направлениям (осям), равные 1. И вектор СВ состоит также из независимых величин. Выбор такой ковариационной матрицы очень удобен, т.к. мы сможем ее сократить в критерии качества Кульбака-Лейблера. Далее, векторы
Мы здесь для
желаемого нормального распределения МО всюду выбрали равные нулю. Это значит,
центр многомерного распределения
Если кто не знает
Итак, мера расхождения двух гауссовых ПРВ у нас есть. И эта мера зависит от векторов МО и дисперсии:
Но кодер на выходе выдает не эти величины, а непосредственно вектор скрытого состояния
Как же нам
вычислять МО и дисперсии текущего распределения и сделать так, чтобы алгоритм
обратного распространения ошибки мог использовать эту информацию при обучении VAE? Для этого
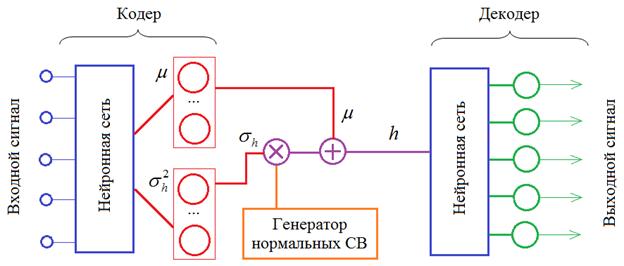
кодер будет формировать не сам вектор h, а векторы
Здесь генератор
НСВ выдает величины с нулевым вектором МО и единичными дисперсиями. Поэтому,
после поэлементного умножения на
То есть, в
процессе обучения нейроны кодера будут выдавать векторы МО и дисперсии для
каждого входного наблюдения
Законы физики «заставляют» ее течь по ложбинке, а не по возвышенностям. Также и при обучении НС: нейроны приобретают те признаки, которым легче обучиться. Структура вариационного автоэнкодера как раз способствует формированию МО и дисперсии на этих группах нейронов. Это естественная магия работы НС. Теперь, имея эти оценки, можно использовать меру Кульбака-Лейблера для определения соответствия текущего распределения заданному, а также еще один критерий для соответствия входного сигнала выходному. То есть, в процессе обучения VAE будут минимизироваться сразу два этих критерия. Первый будет способствовать формированию правильного распределения векторов h скрытого пространства. А второй – соответствию выходного сигнала входному. Здесь можно, например, взять меру минимума среднего квадрата ошибок рассогласования:
где
На следующем занятии мы реализует этот вариационный автоэнкодер и посмотрим к каким результатам он приводит. Курс по нейронным сетям: https://stepik.org/a/227582 Видео по теме |
,
будем требовать от кодера формирования распределения точек на плоскости в
соответствии с двумерной нормальной ПРВ:
:
. Значит,
нам нужен критерий качества, который бы оценивал степень расхождения между
этими двумя распределениями: 
и
-
ковариационные матрицы вектора СВ. Например, для вектора h при условии
независимости его величин, ковариационная матрица будет иметь диагональный вид:
-
математическое ожидание для каждой из k величин:
также
можно будет сократить. В результате, мера Кульбака-Лейблера для нашего частного
случая, станет следующей:
- сумма
значений элементов главной диагонали матрицы (след матрицы);
- определитель
матрицы (для диагональной – произведение значений на главной диагонали).
:
и
сложением с 
,
получим НСВ с этими характеристиками:
. Но
откуда НС будет «знать», что одна группа нейронов – это МО, а другая –
дисперсии? Она такими категориями не «мыслит»! Это происходит по тем же
причинам, по которым, например, река течет строго по своему руслу:
-
вектор входного сигнала; 
-
вектор выходного сигнала. Результирующий критерий будет равен сумме этих двух
величин:
