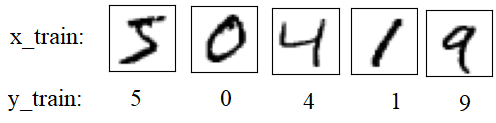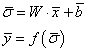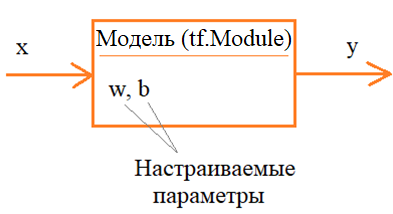
|
Делаем модель с помощью класса tf.Module. Пример обучения простой нейросетиКурс по нейронным сетям: https://stepik.org/a/227582 В машинном обучении задачу оптимизации (поиска решения) можно визуально представить в виде некоторой модели (алгоритма), зависящей от набора настраиваемых параметров:
На вход модели подается входной сигнал x, а на выходе должен формироваться требуемый сигнал y. Модель, как раз, и должна обеспечивать корректное отображение входов x на выходы y. Так, в общем, можно сформулировать задачу параметрической оптимизации. Один
из типовых примеров модели в машинном обучении – это нейронные сети. Обычно,
каждый их слой представляется определенной моделью: полносвязной, сверточной,
рекуррентной и т. п. А чтобы подобрать нужные параметры w,
b, мы должны знать (на этапе
обучения) какие выходы
Если параметры w, b определены неверно, то будем получать неверные выходные значения. Поэтому, для подбора w, bзадается метрика (функция потерь), которая показывает насколько точно входы соответствуют требуемым выходам:
Подобные задачи очень удобно решать с помощью Tensorflowи одну из них мы сейчас рассмотрим. Так как Tensorflowчасто используется для описания нейронных сетей, то в качестве модели реализуем полносвязный (Dense) слой, состоящий из заданного числа нейронов и линейной функцией активации:
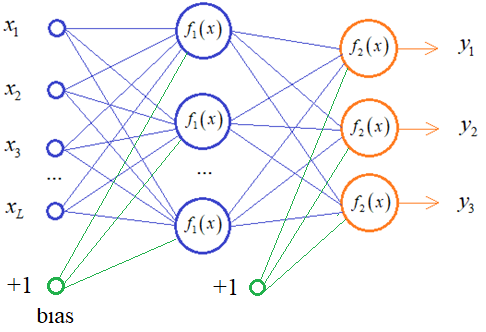
Я буду полагать, что вы знаете базовые основы построения и обучения нейронных сетей. Если это не так, то смотрите плейлист по нейронным сетям на этом канале: Математически полносвязный слой можно описать следующими формулами:
Здесь
W - матрица весовых коэффициентов
связей между входами x
и нейронами слоя; b–вектор
смещений; Так
как мы полагаем линейную функцию активации
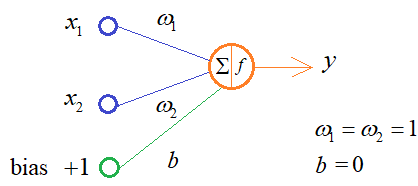
Чтобы обучить Denseслой нейронной сети, нам нужно выбрать конкретную задачу. Пусть это будет сложение двух чисел. Очевидно, здесь достаточно одного нейрона с двумя входами, одним выходом и следующими оптимальными весами связей:
В результате, требуемое выходное значение – это просто сумма двух чисел:
А в качестве меры качества работы НС выберем следующую функцию потерь:
то есть, минимум квадратов ошибок рассогласования. Реализация модели на TensorflowДавайте теперь реализуем такую модель на Tensorflow и проведем ее обучение с помощью алгоритма градиентного спуска. Вначале выполним импорт пакетов: import os os.environ['TF_CPP_MIN_LOG_LEVEL'] = '2' import tensorflow as tf А, затем, определим класс модели полносвязного слоя НС: class DenseNN(tf.Module): def __init__(self, outputs): super().__init__() self.outputs = outputs self.fl_init = False def __call__(self, x): if not self.fl_init: self.w = tf.random.truncated_normal((x.shape[-1], self.outputs), stddev=0.1, name="w") self.b = tf.zeros([self.outputs], dtype=tf.float32, name="b") self.w = tf.Variable(self.w) self.b = tf.Variable(self.b) self.fl_init = True y = x @ self.w + self.b return y Смотрите, мы здесь вначале создаем класс на основе базового класса tf.Module, который предоставляет дополнительный функционал для реализации модели. Далее, в конструкторе вызываем конструктор базового класса и инициализируем два локальных свойства: outputs – число выходов слоя (число нейронов); fl_init – флаг начальной инициализации весовых коэффициентов (параметров модели). Затем, определяем магический метод __call__, который превратит наш класс DenseNN в функтор (то есть, мы его сможем использовать подобно функции). В качестве параметра будем передавать вектор x входного сигнала. Потом, ниже идет проверка на наличие начальной инициализации. Если ее еще не было, то мы создаем набор параметров w в виде двумерной матрицы размерностью: число входов x число выходов и вектор b (смещения, bias) для параметров смещений каждого нейрона с начальными нулевыми значениями. После этого вычисляются выходные значения нейронов слоя и возвращаются методом __call__. Теперь, мы можем создать эту модель: model = DenseNN(1) и вызвать для любого тензора, размерностью 1x2: print(model(tf.constant([[1.0, 2.0]])) ) Модель из одного нейрона и линейной функцией активации создана, далее нам нужно определить набор обучающих данных, например, так: x_train = tf.random.uniform(minval=0, maxval=10, shape=(100, 2)) y_train = [a + b for a, b in x_train] Затем, зададим функцию потерь и оптимизатор для градиентного спуска: loss = lambda x, y: tf.reduce_mean(tf.square(x - y)) opt = tf.optimizers.Adam(learning_rate=0.01) Теперь можно запускать непосредственно алгоритм обучения нашей модели. Его можно записать, следующим образом: EPOCHS = 50 for n in range(EPOCHS): for x, y in zip(x_train, y_train): x = tf.expand_dims(x, axis=0) y = tf.constant(y, shape=(1, 1)) with tf.GradientTape() as tape: f_loss = loss(y, model(x)) grads = tape.gradient(f_loss, model.trainable_variables) opt.apply_gradients(zip(grads, model.trainable_variables)) print(f_loss.numpy()) В принципе, здесь все должно быть вам уже знакомым. Первый цикл перебирает обучающую выборку 50 раз (50 эпох), а вложенный выбирает наблюдения в виде двумерного вектора 1x2, для которых вычисляются градиенты и применяются к тренировочным параметрам. Обратите внимание, мы в методах gradient и apply_gradients указываем список параметров как model.trainable_variables. Эта коллекция (кортеж) формируется автоматически базовым классом tf.Module, что очень удобно для дальнейшей реализации. Для всех тренировочных параметров (w, b) мы вычисляем градиенты и применяем их, изменяя эти параметры. В конце программы выведем список значений параметров w, b, чтобы убедиться в их правильном подборе: print(model.trainable_variables) После запуска программы, увидим значения: (<tf.Variable 'Variable:0' shape=(1,) dtype=float32, numpy=array([6.0594943e-05], dtype=float32)>, <tf.Variable 'Variable:0' shape=(2, 1) dtype=float32, numpy=array([[0.9999934], [0.9999947]], dtype=float32)>) То есть, параметр b = 0, а весовые коэффициенты w почти 1, что очень близко к оптимальным величинам. Модель для сложения двух чисел была обучена успешно. ИтогиДавайте еще раз посмотрим, что же мы сделали в этой программе. Определили модель, сформировали обучающую выборку, задали функцию потерь и оптимизатор для обучения модели. В конце записали цикл градиентного спуска для нахождения требуемых параметров w, b:
Я здесь цикл обучения представил методом fit модели. Те из вас, кто работал с пакетом Keras, сразу заметят сходство нашего алгоритма с аналогичной реализацией на Keras. И это не удивительно, так как Keras – надстройка над Tensorflow, представляющий лишь удобный API-интерфейс для реализации нейронных сетей. Здесь же мы опустились на уровень ниже и сделали все непосредственно на Tensorflow. Но зачем было все так усложнять? Почему бы не оставаться на уровне Keras? В данном случае именно так и следовало поступить. Но это был лишь пример реализации модели на Tensorflow и я его специально взял простым, чтобы все было предельно понятно. Бывают ситуации, когда функционала Keras недостаточно. Например, при реализации обучения генеративно-состязательных сетей. В таких задачах уже приходится использовать Tensorflow в «чистом виде», а потому полезно знать, как все это работает. Курс по нейронным сетям: https://stepik.org/a/227582 Видео по теме |
должны
получаться при заданных входах 
.
Часто для этого формируется обучающая выборка, в которой каждому наблюдению x
поставлено в соответствие правильное значение y
(задача обучения с учителем). Например, на вход подаются изображения цифр (сигнал
x), а на выходе должно формироваться
одно из значений от 0 до 9:
-
функция активации нейрона (общая для всего слоя); y–вектор
выходных значений нейронов.
,
то эти две формулы можно заменить одной:
