Расширенный вариационный автоэнкодер (CVAE)Курс по нейронным сетям: https://stepik.org/a/227582 На предыдущем занятии мы с вами реализовали простой вариационный автоэнкодер и увидели его способность формировать компактное скрытое пространство и декодировать его значения обратно в исходный сигнал. При этом некоторые изображения цифр были представлены не очень полно, а другие могли и вовсе отсутствовать. То есть, скрытое пространство не достаточно полно описывало входной сигнал. Конечно, в первую очередь, это ограниченность его размера – всего два элемента (двумерное пространство). Увеличивая, можно получать лучшее представление входов в векторах скрытого пространства:
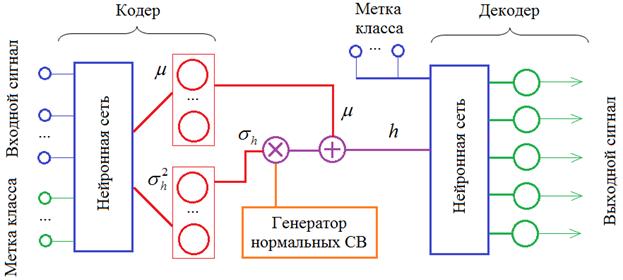
Но есть и другой путь. Наша обучающая выборка изображений цифр снабжена метками класса, то есть, указанием того, какая цифра нарисована. Мы можем использовать эту дополнительную информацию и передавать ее кодеру и декодеру:
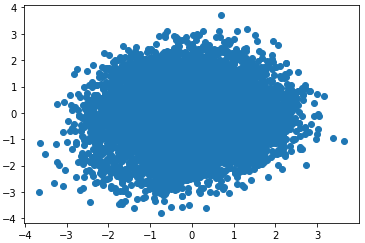
Назовем такую схему расширенным вариационным автоэнкодером. В англоязычной литературе он носит название: Conditional Variational Autoencoder (CVAE) Хорошая статья по этому алгоритму представлена на странице: https://habr.com/ru/post/331664/ Давайте реализуем этот автоэнкодер. Я возьму его структуру из предыдущего занятия и только добавлю входы меток у кодера и декодера: # импорт модулей и подготовка данных import numpy as np import matplotlib.pyplot as plt from tensorflow.keras.datasets import mnist from tensorflow import keras import keras.backend as K from keras.layers import Dense, Flatten, Reshape, Input, Lambda, BatchNormalization, Dropout from keras.layers import concatenate hidden_dim = 2 num_classes = 10 batch_size = 100 # должно быть кратно 60 000 и 10 0000 (x_train, y_train), (x_test, y_test) = mnist.load_data() # стандартизация входных данных x_train = x_train / 255 x_test = x_test / 255 x_train = np.reshape(x_train, (len(x_train), 28, 28, 1)) x_test = np.reshape(x_test, (len(x_test), 28, 28, 1)) y_train_cat = keras.utils.to_categorical(y_train, num_classes) y_test_cat = keras.utils.to_categorical(y_test, num_classes) # построение структуры сети def dropout_and_batch(x): return Dropout(0.3)(BatchNormalization()(x)) input_img = Input(shape=(28, 28, 1)) fl = Flatten()(input_img) lb = Input(shape=(num_classes,)) x = concatenate([fl, lb]) x = Dense(256, activation='relu')(x) x = dropout_and_batch(x) x = Dense(128, activation='relu')(x) x = dropout_and_batch(x) z_mean = Dense(hidden_dim)(x) z_log_var = Dense(hidden_dim)(x) def noiser(args): global z_mean, z_log_var z_mean, z_log_var = args N = K.random_normal(shape=(batch_size, hidden_dim), mean=0., stddev=1.0) return K.exp(z_log_var / 2) * N + z_mean h = Lambda(noiser, output_shape=(hidden_dim,))([z_mean, z_log_var]) input_dec = Input(shape=(hidden_dim,)) lb_dec = Input(shape=(num_classes,)) d = concatenate([input_dec, lb_dec]) d = Dense(128, activation='elu')(d) d = dropout_and_batch(d) d = Dense(256, activation='elu')(d) d = dropout_and_batch(d) d = Dense(28*28, activation='sigmoid')(d) decoded = Reshape((28, 28, 1))(d) encoder = keras.Model([input_img, lb], h, name='encoder') decoder = keras.Model([input_dec, lb_dec], decoded, name='decoder') cvae = keras.Model([input_img, lb, lb_dec], decoder([encoder([input_img, lb]), lb_dec]), name="cvae") Мы здесь используем новый слой concatenate, который просто объединяет два входных узла в единый узел для передачи его уже на полносвязный слой нейронов. Все остальное вам здесь должно быть уже известно. Еще раз отмечу, что расширенный автоэнкодер (cvae) строится на основе кодера (encoder) и декодера (decoder). То есть, это все одна и та же сеть, а не три различных. Поэтому, обучая автоэнкодер, мы автоматически обучаем и кодер с декодером. Далее, абсолютно также определяем функцию потерь, компилируем сеть и производим ее обучение: def vae_loss(x, y): x = K.reshape(x, shape=(batch_size, 28*28)) y = K.reshape(y, shape=(batch_size, 28*28)) loss = K.sum(K.square(x-y), axis=-1) kl_loss = -0.5 * K.sum(1 + z_log_var - K.square(z_mean) - K.exp(z_log_var), axis=-1) return (loss + kl_loss)/2/28/28 cvae.compile(optimizer='adam', loss=vae_loss) cvae.fit([x_train, y_train_cat, y_train_cat], x_train, epochs=5, batch_size=batch_size, shuffle=True) В процессе обучения дополнительно передаем на входы метки классов. Смотрим, на распределение полученных точек скрытого пространства: lb = lb_dec = y_test_cat h = encoder.predict([x_test, lb, lb_dec], batch_size=batch_size) plt.scatter(h[:, 0], h[:, 1])
И на наборы изображений на выходе декодера: n = 4 total = 2*n+1 input_lbl = np.zeros((1, num_classes)) input_lbl[0, 2] = 1 plt.figure(figsize=(total, total)) h = np.zeros((1, hidden_dim)) num = 1 for i in range(-n, n+1): for j in range(-n, n+1): ax = plt.subplot(total, total, num) num += 1 h[0, :] = [1*i/n, 1*j/n] img = decoder.predict([h, input_lbl]) plt.imshow(img.squeeze(), cmap='gray') ax.get_xaxis().set_visible(False) ax.get_yaxis().set_visible(False)
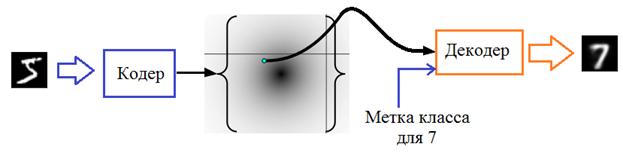
Смотрите, передавая декодеру метку изображений цифры 2, он интерпретирует каждую точку скрытого пространства как различные изображения двоек. Если мы укажем метку другой цифры, то увидим множество ее изображений. То есть, одна и та же точка (вектор) скрытого пространства интерпретируется декодером в соответствии с меткой класса. И это очень здорово! Во-первых, мы получаем удобный инструмент для генерации изображений строго определенного типа. И, во-вторых, мы можем для любой цифры на входе кодера, получать желаемые начертания любой другой цифры на выходе декодера:
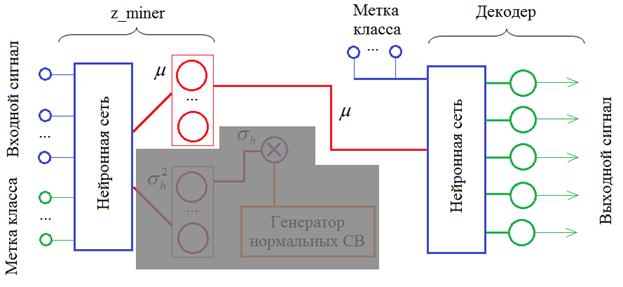
Если нам при этом не важно получаемое распределение точек скрытого пространства, то можно сделать атоэнкодер усеченной структуры:
Мы здесь вместо классического кодера, который на выходе выдавал МО и дисперсию, оставим только МО для переданного входного сигнала. Далее, это среднее значение (центр ПРВ) подается на вход декодера (вместе с новой, другой меткой класса) и на выходе получаем интерпретацию декодером точки пространства:
Давайте посмотрим как это будет работать. Сначала опишем структуру такого автоэнкодера: z_meaner = keras.Model([input_img, lb], z_mean) tr_style = keras.Model([input_img, lb, lb_dec], decoder([z_meaner([input_img, lb]), lb_dec]), name='tr_style') А, затем, для различных входных цифр 5 посмотрим на результат декодирования других цифр: def plot_digits(*images): images = [x.squeeze() for x in images] n = min([x.shape[0] for x in images]) plt.figure(figsize=(n, len(images))) for j in range(n): for i in range(len(images)): ax = plt.subplot(len(images), n, i*n + j + 1) plt.imshow(images[i][j]) plt.gray() ax.get_xaxis().set_visible(False) ax.get_yaxis().set_visible(False) plt.show() dig1 = 5 num = 10 X = x_train[y_train == dig1][:num] lb_1 = np.zeros((num, num_classes)) lb_1[:, dig1] = 1 plot_digits(X) for i in range(num_classes): lb_2 = np.zeros((num, num_classes)) lb_2[:, i] = 1 Y = tr_style.predict([X, lb_1, lb_2], batch_size=num) plot_digits(Y) Здесь вначале объявляется вспомогательная функция для вывода серии изображений с выхода декодера, а затем, делаем цикл по меткам для 10 цифр. Тензор Y будет содержать изображения при декодировании и, затем, они выводятся на экран. Результат работы будет следующий:
Смотрите как декодер интерпретирует одни и те же точки скрытого пространства для разных меток класса. Их начертание, стилистика примерно одинаковы для разных цифр. И это потрясающий результат! Получается, что каждый конкретный вектор скрытого пространства:
описывает некие единые, общие характеристики различных изображений. В частности, наклон, толщину линий, какие-то особенные начертания. Здесь даже сложно подобрать правильные слова: неуловимые особенности корректно представляются компактным скрытым пространством. Это означает, что мы можем сложные входные данные самых разных размерностей отображать в пространство с гораздо меньшими размерами и каждая точка этого скрытого пространства будет определять вполне определенные характерные свойства входного сигнала. Именно так, в целом следует понимать работу кодера и декодера в автоэнкодере. Примеры с изображениями цифр – это всего лишь один маленький, частный пример. Область использования вариационных автоэнкодеров куда шире. Например, на движущийся объект (робот) можно поставить камеру и кадры потокового видео (того, что видит робот) переводить в скрытое пространство признаков. И, далее, уже по ним принимать решения что делать роботу дальше. Это гораздо лучше, чем пытаться напрямую анализировать каждый кадр.
Вот что из себя представляют различные типы автоэнкодеров. Курс по нейронным сетям: https://stepik.org/a/227582 Видео по теме |