|
Keras - обучение сети распознаванию рукописных цифрКурс по нейронным сетям: https://stepik.org/a/227582 На предыдущем занятии мы с вами познакомились с пакетом Keras, создали и обучили простейшую НС для перевода градусов Цельсия в градусы Фаренгейта. Пришло время сделать что-то по-настоящему интересное. И на этом занятии мы обучим сеть распознавать рукописные цифры. Здесь сразу возникает два вопроса: где взять обучающую выборку и какую структуру НС выбрать? На первый вопрос, как ни странно, ответ будет очень простым: мы воспользуемся уже готовой выборкой из уже подготовленной БД изображений: MNIST – (сокращение от «Modified National Institute of Standards and Technology») – база данных образцов рукописного написания цифр Эта библиотека образцов поставляется вместе с Keras и для доступа к ней нужно выполнить следующий импорт: from tensorflow.keras.datasets import mnist А, затем, загрузить их: (x_train, y_train), (x_test, y_test) = mnist.load_data() Здесь 60 000 изображений в обучающей выборке и 10 000 – в тестовой. Мы будем использовать определения:
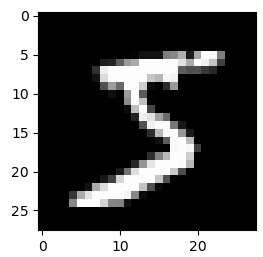
Каждое изображение имеет размер 28х28 пикселей и представлено в градациях серого, т.е. каждый пиксел имеет значение от 0 до 255 (0 – черный цвет, 255 – белый):
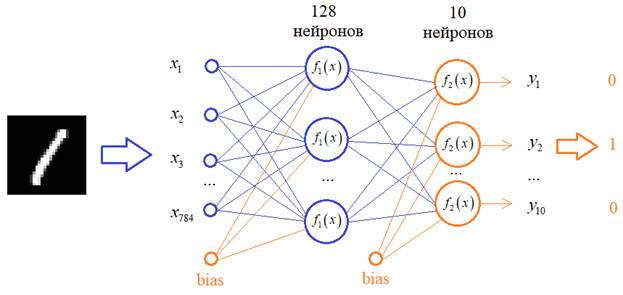
Давайте выведем первые 25 изображений из этой базы: # отображение первых 25 изображений из обучающей выборки plt.figure(figsize=(10,5)) for i in range(25): plt.subplot(5,5,i+1) plt.xticks([]) plt.yticks([]) plt.imshow(x_train[i], cmap=plt.cm.binary) plt.show() Видим самые разные цифры с произвольным написанием. Все их НС должна научиться правильно распознавать. Теперь нужно ответить на второй вопрос о структуре сети. Строгого ответа на него нет, т.к. структура выбирается самим разработчиком исходя из его представлений о решении этой задачи. Общий ориентир здесь такой: для распознавания графических образов хорошо себя показали сверточные НС. Но мы о них пока еще ничего не знаем, поэтому воспользуемся обычной полносвязной НС с
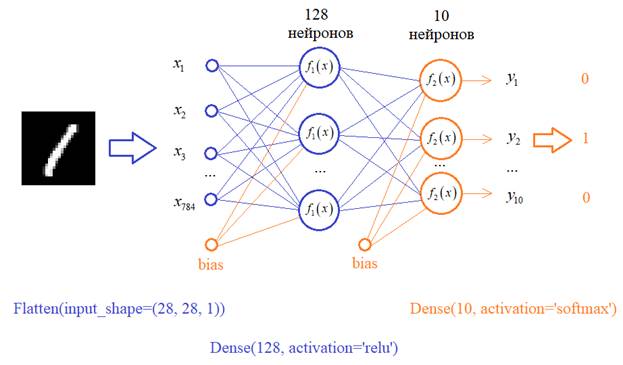
В качестве функций активации скрытого слоя выберем популярную на сегодняшний день ReLu, а у выходных нейронов – softmax, т.к. мы хотим интерпретировать выходные значения в терминах вероятности принадлежности к тому или иному классу цифр. У вас может возникнуть вопрос: почему структура сети именно такая? Почему именно 128 нейронов и один скрытый слой? Да, в общем-то не почему. Просто, мне так захотелось. Вы можете, для примера, взять 100 нейронов или 50 или построить сеть с двумя скрытыми слоями и так далее. Это, на сегодняшний день, делается на уровне шаманства, интуиции разработчика НС. Я решил вот так. Реализуем эту сеть. Первый слой должен преобразовывать изображение 28x28 пикселей в вектор из 784 элементов. Для такой операции в Keras можно создать слой специального вида – Flatten и в нашем случае мы его пропишем так:
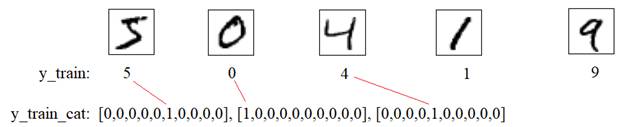
Следующий слой создадим с помощью уже известного нам класса Dense, который свяжет все 784 входа со всеми 128 нейронами. И такой же последний слой из 10 нейронов, который будет связан со всеми 128 нейронами предыдущего слоя. Итоговую модель в Keras можно записать так: model = keras.Sequential([ Flatten(input_shape=(28, 28, 1)), Dense(128, activation='relu'), Dense(10, activation='softmax') ]) print(model.summary()) # вывод структуры НС в консоль Все, структура сети определена, обучающий набор изображений имеется. Что нужно сделать с этими изображениями до момента обучения? Помните, мы говорили, что желательно входные значения вектора x стандартизировать так, чтобы они находились в диапазоне от 0 до 1? Это мы сейчас и сделаем вот такими строчками: x_train = x_train / 255 x_test = x_test / 255 Здесь каждое значение тензоров x_train и x_test будет делиться на максимальное число 255, которое они могут принимать. На выходе получим вещественные величины от 0 до 1. Еще нам нужно подготовить правильный формат выходных значений. Опять же, для каждого изображения цифры вектор y_train содержит число:
А нам нужен вектор с 1 на месте соответствующего числа, т.к. наша НС имеет 10 выходов, и каждый выход будет соответствовать определенной цифре: от 0 до 9. Так как это типовое преобразование, то в Keras уже имеется функция, которая все это делает. Нам достаточно записать строчки: y_train_cat = keras.utils.to_categorical(y_train, 10) y_test_cat = keras.utils.to_categorical(y_test, 10) чтобы получить наборы векторов y_train_cat и y_test_cat по заданному формату. Здесь второй параметр 10 – это размерность каждого вектора. Отлично, данные подготовлены. Теперь выберем функцию потерь (loss function) и способ оптимизации градиентного алгоритма. И вот как раз здесь нам понадобится та скучная теория прошлых занятий. Помните, мы говорили, что в задачах классификации лучше всего начинать с категориальной кросс-энтропии: categorical_crossentropy и активационной функции выходных нейронов softmax. Функцию активации мы уже такую прописали, осталось указать этот критерий качества: model.compile(optimizer='adam', loss='categorical_crossentropy', metrics=['accuracy']) Здесь же мы указываем оптимизацию по Adam и еще некую метрику. Что это за метрика и зачем она нужна? Смотрите, в действительности при решении задач классификации нам важно не значение какой-то кросс-энтропии, а процент правильно распознанных цифр. Но построить алгоритм, который бы минимизировал именно процент ошибок сложно (если вообще возможно), поэтому мы привязываемся к более простому с точки зрения математики критерию – категориальной кросс-энтропии, минимизируя которую, надеемся, что будет уменьшаться и процент ошибок, что в общем-то и происходит. Поэтому metrics здесь – это та метрика, которая нужна заказчику и мы ее можем отслеживать в процессе обучения и тестирования НС. Все, на данном этапе, мы полностью подготовили сеть и данные для запуска процесса обучения. Запишем знакомую нам уже команду: model.fit(x_train, y_train_cat, batch_size=32, epochs=10, validation_split=0.2) и здесь появились новые параметры:
Давайте ниже, сразу, выполним проверку работы сети на тестовом множестве: model.evaluate(x_test, y_test_cat) Метод evaluate прогоняет все тестовое множество и вычисляет значение критерия качества и метрики. Кроме того, давайте выполним распознавания какого-либо тестового изображения: n = 1 x = np.expand_dims(x_test[n], axis=0) res = model.predict(x) print( res ) Здесь мы сначала выделяем из тензора n-е изображение и, затем, прогоняем его по сети, используя метод predict. На выходе получим 10 значений, по которым, затем, нужно будет определить правильность классификации цифр. Запустим эту программу и, смотрите, мы видим вектор выходных значений: [[3.2027703e-05 4.2498193e-04 9.9881822e-01 4.3836111e-04 1.3467245e-09
И полагаем, что максимальное значение как раз и будет соответствовать нужному классу. В данном случае – это число 9.9881822e-01 третьего выхода, то есть, для цифры 2. Чтобы было проще воспринимать выходную информацию, будем выводить номер максимального числа из этого вектора. Для этого воспользуемся довольно удобной функцией argmax модуля numpy: print( np.argmax(res) ) И, еще, отобразить на экране это тестовое изображение: plt.imshow(x_test[n], cmap=plt.cm.binary) plt.show() Запускаем программу, видим число 2 и картинку с изображением этой цифры. Нейронная сеть верно распознала эту картинку. Давайте теперь выделим и посмотрим на неверные результаты распознавания. Пропустим через НС всю тестовую выборку и векторы выходных значений преобразуем в числа от 0 до 9: pred = model.predict(x_test) pred = np.argmax(pred, axis=1) print(pred.shape) print(pred[:20]) print(y_test[:20]) Затем, сформируем маску, которая будет содержать True для верных вариантов и False – для неверных. И с помощью этой маски выделим из тестовой выборки все неверные результаты: mask = pred == y_test print(mask[:10]) x_false = x_test[~mask] y_false = x_test[~mask] print(x_false.shape) И выведем первые 5 из них на экран: for i in range(5): print("Значение сети: "+str(y_test[i])) plt.imshow(x_false[i], cmap=plt.cm.binary) plt.show() Вот мы с вами сделали следующий шаг к более сложной реализации НС для распознавания рукописных цифр. Попробуйте самостоятельно повторить этот пример и поиграться с разным числом нейронов скрытого слоя: посмотрите как это будет сказываться на результатах классификации. А на следующем занятии мы поподробнее поговорим о способе оптимизации на основе стохастического градиента и дополнительных вариантах разделения обучающей выборки на собственно обучающую и проверочную. Курс по нейронным сетям: https://stepik.org/a/227582 Видео по теме |