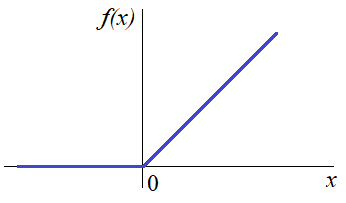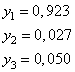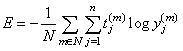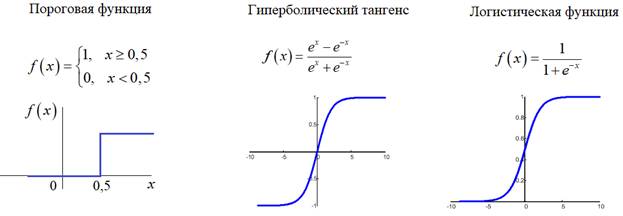
|
Функции активации, критерии качества работы НСПродолжаем рассматривать необходимые теоретические моменты построения и обучения НС и следующий важный вопрос – выбор функций активации нейронов. Обычно, они едины для всех нейронов скрытых слоев, исключения могут составлять нейроны выходного слоя. Но, все же, какие функции активации выбирать? На предыдущих занятиях мы с вами уже коснулись пороговой функции, гиперболического тангенса и логистической функции:
Эти три функции достались нам еще от «отцов основателей» НС. Они вполне работоспособны при небольшом числе скрытых слоев: до 7-8. Кроме первой: она иногда применяется для нейронов выходного слоя в задачах классификации, независимо от числа слоев НС. Но почему гиперболический тангенс и логистическая функция не подходят для больших НС? Это связано, прежде всего, с алгоритмом обучения back propagation. Если вы вспомните наше занятие о нем, то локальный градиент следующих с конца нейронов вычисляется примерно так:
Учитывая, что
получим:
В этой формуле я хотел показать только одно: локальный градиент нейронов следующего слоя вычисляется через произведение двух производных функции активации. Хорошо, ну и что с того? Дело вот в чем. Максимальное значение производных гиперболического тангенса или логистической функции меньше единицы. Например, для логистической функции:
но, так как
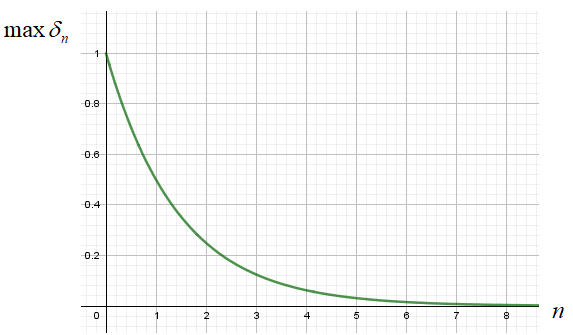
то произведения таких производных образуют затухающую экспоненту:
Здесь n можно воспринимать как число слоев в НС и из графика видно, что уже при 8 слоях максимальное значение локального градиента почти равно нулю. О чем это нам говорит? Это говорит о том, что весовые коэффициенты будут активно меняться для выходных слоев и почти оставаться неизменными для начальных. То есть, первые слои практически будут отброшены из процесса обучения. Вот такой «сюрприз» готовят нам логистическая и гиперболическая функции активации. Чтобы решить эту проблему, нужно выбрать функцию, производная которой была бы равна 1. Что это за функция? Да – это просто
Если мы теперь сделаем ограничения по нижнему значению, например, по нулю:
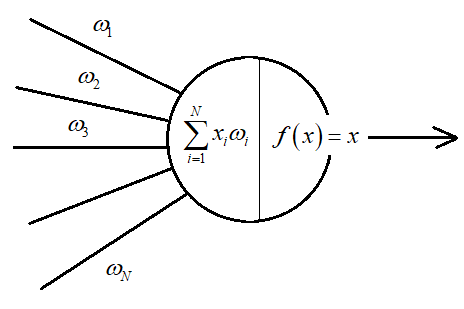
то получим активационную функцию под названием ReLu: Это одна из самых популярных функций активации на сегодняшний день и, кроме того, не уменьшает локальные градиенты при переходе от слоя к слою. Поэтому часто используется при deep learning – обучении НС с большим числом слоев Рекомендация обучения №8: при малом числе слоев можно использовать гиперболическую и сигмоидальную функции активации или ReLu, при числе слоев от 8 и более – ReLu и ее вариации. Однако, для выходного слоя функция активация часто меняется и выбирается другой. Например, в задачах регрессии, где нужно получить какое-то числовое значение функции (это может быть прогноз или оценка параметра или еще что-то) используют линейную функцию активации: linear которая просто возвращает входную сумму на выходном нейроне сети:
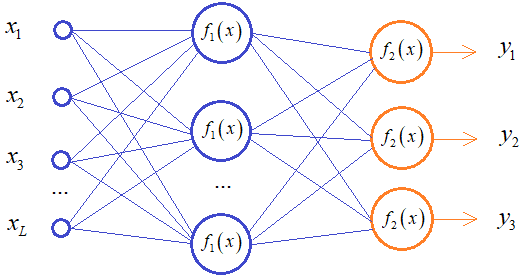
В другом случае, в задачах классификации (например, марок машин) для не пересекающихся классов, выходной слой содержит несколько нейронов, каждый из которых активизируется для своего строго определенного класса:
Например:
Предъявляя сети вектор:
например, для шкоды, мы бы хотели, чтобы выходные значения были равны:
В этом случае, для каждого входного вектора обучающей выборки, выходные значения также являются вектором:
Так вот, в таких задачах было бы хорошо выходные значения интерпретировать как вероятности соотнесения входного вектора к тому или иному классу, то есть, на выходе получать значения от 0 до 1, которые можно было бы воспринимать как вероятности. Например:
Причем, в сумме
они должны давать 1. Как это сделать? То есть, как выбрать функцию
Теперь, чтобы представить эти величины в терминах вероятности, выполняется преобразование:
Оно получило название softmax В результате, НС нам выдает как бы вероятности определения того или иного класса по значениям входного вектора. Но, все же, это не вероятности в чистом виде – это лишь некоторое приближение, способ интерпретации выходных данных в терминах вероятностей, не более того. И чтобы сама сеть корректно могла обучаться при таких выходах, она должна иметь адекватный критерий качества. Здесь хорошо подходит мера, известная как перекрестная энтропия:
где N – размер
обучающей выборки; Рекомендация обучения №9: для задач регрессии у выходных нейронов использовать линейную (linear) функцию активации, для задач классификации не пересекающихся классов – softmax. Критерии качестваПоследнее, что нам необходимо знать для корректной реализации процесса обучения НС – критерии качества. Как мы не раз отмечали, в классическом варианте алгоритма back propagation критерием является минимум средних квадратов ошибок между требуемыми выходными значениями НС и реальными:
Здесь Но, как показала практика, этот критерий подходит далеко не для всех задач, где применяются НС и методом проб и ошибок были найдены другие, приводящие к более лучшим результатам. Мы рассмотрим следующие:
Распознавание:
Обработка текста:
Задачи регрессии:
Может быть, для некоторых из вас, стало откровением такое разнообразие критериев качества? Да и как их выбрать, какие рекомендации? Общие ориентиры я сейчас укажу, по крайней мере те, что известны мне. Но это лишь ориентиры. В каждом конкретном случае все равно придется делать выбор, исходя из некого «здравого смысла» и собственного опыта. Другого пути нет. Вам никто сегодня точно не скажет: сделай то-то и то-то и получишь лучший результат. Такого просто нет. Построение и, тем более, обучение НС – это очень субъективный, творческий процесс. Здесь помогает только опыт и базовые знания о том, как все это работает. Вот о знаниях сейчас и пойдет речь, ну а опыт, как всегда, это дело индивидуальное и только вы сами можете его приобрести. Сначала рассмотрим критерии для задач регрессии, где выходное значение нейрона представлено в числовой шкале (цены, рост, вес, количества и т. п.). Здесь первый критерий – это классический средний квадрат ошибок:
Его недостаток в том, что он образует множество локальных минимумов и часто обучение в них и застревает. Кроме того, этот критерий резко возрастает при появлении больших ошибок, т.к. ошибка возводится в квадрат. Значимые ошибки, как правило, встречаются редко, но если уж появились, то это сильно скажется на критерии качества. Как вариант, можно воспользоваться средней суммой модулей ошибок (mean absolute error):
В этом случае большие, редкие ошибки уже не так сильно влияют на величину E. Возможно, некоторые из вас заметят, что функция модуля не имеет производной в нижней точке. Но, это уже не проблема, численно ее можно определить с некоторыми допущениями. Поэтому такой критерий качества тоже применяется на практике. Следующий критерий качества средний квадрат логарифмических ошибок (mean squared logarithmic error):
В отличие от обычной суммы квадратов использование логарифмов значительно уменьшает редкие ошибки и они уже не так сильно влияют на величину E. Это еще один способ борьбы с редкими, но значимыми ошибками на выходе НС. Далее, для задач прогнозирования выполняют нормировку суммы модулей и используют критерий под названием «средний абсолютный процент ошибок» (mean absolute percentage error):
Например, НС выдает абсолютную ошибку 1000. Это много или мало? Здесь важно знать относительно каких величин получается 1000. Если мы оперируем величинами 10 000 000, то 1000 – это ошибка в доли процента. А если используются значения порядка 10 000, то 1000 – это уже ошибка в 10%. Чтобы уйти от абсолютных величин и перевести ошибку в относительные – проценты, как раз и ввели такой критерий качества. Следующие критерии применяются в задачах классификации (распознавания). Предположим, что НС имеет несколько выходов M, на каждом из которых появляются значения +1 или -1, то есть:
Здесь в качестве критерия качества можно воспользоваться мерой hinge или square hinge (хиндж):
Он работает очевидным образом. Если НС правильно выдает значение, т.е.
то
иначе, на выходе будем получать 2:
Фактически, мы здесь увеличиваем параметр E при каждом несовпадении выхода с заданным значением. На сегодняшний день в задачах классификации образов при двух классах (например, классификация на мужчин и женщин, собак и кошек и т. п.), широко используется бинарная кросс-энтропия (binary crossentropy):
При этом,
требуемые выходы отмечаются бинарными значениями: Наконец, считается, что при обработке текста хорошо подходит критерий логарифмический гиперболический косинус (logcosh):
Величина Это лишь некоторые часто используемые на практике критерии качества работы НС. Постоянно появляются все новые и новые варианты. Возможно, вы будете одним из тех, кто придумает очередную популярную меру и о ней начнут говорить на курсах по обучению НС. На этом мы завершим общий теоретический обзор основных моментов для подготовки НС к процессу обучения и далее будем использовать эти знания при решении конкретных практических задач. Видео по теме |
- шкода; 
-
тойота; 
-
форд
,
которая бы выдавала такие величины? Очевидно, что мы должны исходить из сумм на
каждом выходном нейроне:
-
требуемые выходы для m-го входного вектора и j-го выхода сети;
-
реальное значение j-го выхода.
-
требуемые отклики для каждого i-го входного вектора; 
-
получаемый отклик сети, при предъявлении i-го вектора
наблюдений. То есть, мы подбираем весовые коэффициенты связей между нейронами
так, чтобы минимизировать этот функционал.
или
.
Однако, при большем числе классов 
уже
следует выбирать категориальную кросс-энтропию (categorical crossentropy).
близка
к 
при
малых x и примерно
равна 
-
при больших x.
