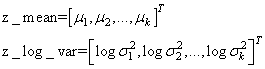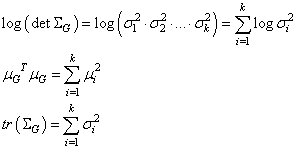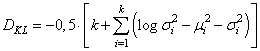|
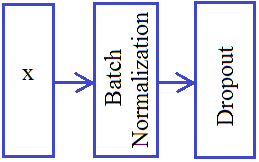
Делаем вариационный автоэнкодер (VAE) в KerasКурс по нейронным сетям: https://stepik.org/a/227582 На предыдущем занятии мы с вами разобрали принцип построения вариационного автоэнкодера. Пришло время его реализовать в пакете Keras. Вначале, как и ранее, подключим необходимые модули и подготовим входную обучающую и тестовую выборки: import numpy as np import matplotlib.pyplot as plt from tensorflow.keras.datasets import mnist from tensorflow import keras import keras.backend as K from tensorflow.keras.layers import Dense, Flatten, Reshape, Input, Lambda, BatchNormalization, Dropout (x_train, y_train), (x_test, y_test) = mnist.load_data() x_train = x_train / 255 x_test = x_test / 255 x_train = np.reshape(x_train, (len(x_train), 28, 28, 1)) x_test = np.reshape(x_test, (len(x_test), 28, 28, 1)) Далее, определим размер векторов скрытого пространства, размер пакета (батча) и вспомогательную функцию для применения слоев Dropout и Batch Normalization к нашей НС: hidden_dim = 2 batch_size = 60 # должно быть кратно 60 000 def dropout_and_batch(x): return Dropout(0.3)(BatchNormalization()(x)) Я думаю, вы помните, какую роль играют эти слои? Они нужны для уменьшения эффекта переобучения и повышения обобщающих свойств нейронов в сети. В литературе по вариационным автоэнкодерам они часто упоминаются, хотя в каждой конкретной реализации нужно смотреть: нужны они или нет. Я здесь их привел больше в качестве примера. Также обратите внимание, что они определяются по принципу графа:
Это очень удобный инструмент в Keras, особенно когда нужно создать сеть произвольной архитектуры. Далее, формируем сеть кодера: input_img = Input((28, 28, 1)) x = Flatten()(input_img) x = Dense(256, activation='relu')(x) x = dropout_and_batch(x) x = Dense(128, activation='relu')(x) x = dropout_and_batch(x) z_mean = Dense(hidden_dim)(x) z_log_var = Dense(hidden_dim)(x) Опять же, используя принцип графов, мы определяем две группы нейронов полносвязного слоя, размерностью hidden_dim (это параметр k из предыдущего занятия). Вектор z_mean – это МО, а вектор z_log_var – логарифм дисперсий (логарифм взят для удобства дальнейших вычислений):
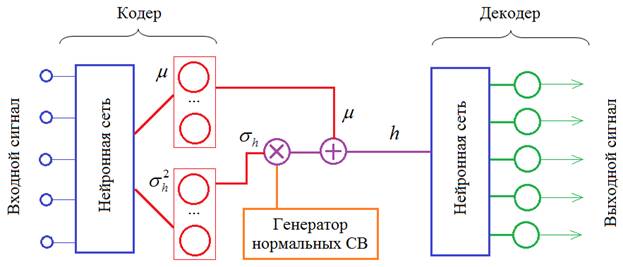
Затем, нам нужно используя величины z_mean и z_log_var сформировать вектор h как нормальную СВ с этими характеристиками. Для этого мы добавим специальный слой Lambda который на входе будет брать два тензора: z_mean, z_log_var: (batch_size, hidden_dim) и на выходе формировать тензор: h: (batch_size, hidden_dim) по общей формуле:
Это делается так. Сначала объявим функцию, которая формирует искомый тензор h: def noiser(args): global z_mean, z_log_var z_mean, z_log_var = args N = K.random_normal(shape=(batch_size, hidden_dim), mean=0., stddev=1.0) return K.exp(z_log_var / 2) * N + z_mean В этой функции мы используем уже имеющиеся глобальные переменные z_mean, z_log_var и переопределяем их, присваивая конкретные числовые значения (args будет содержать тензоры с числами в процессе работы сети). Затем, мы генерируем тензор нормальных СВ с нулевым МО и единичной дисперсией. На выходе формируем тензор h, умножая случайные величины на тензор СКО и прибавляя тензор МО. Здесь операция K.exp(z_log_var / 2) выделяет СКО из логарифма дисперсии:
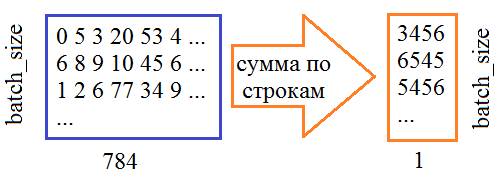
Теперь у нас все готово для создания Lambda-слоя: h = Lambda(noiser, output_shape=(hidden_dim,))([z_mean, z_log_var]) На его вход подаются два тензора, на выходе получаем тензор случайных величин h. Обратите внимание, что здесь z_mean, z_log_var пока еще ссылки на слои НС, а не тензоры с числовыми значениями. То есть, мы пока определяем граф нашего VAE. Далее, определяем слои для декодера. Здесь все достаточно просто и очевидно: input_dec = Input(shape=(hidden_dim,)) d = Dense(128, activation='relu')(input_dec) d = dropout_and_batch(d) d = Dense(256, activation='relu')(input_dec) d = dropout_and_batch(d) d = Dense(28*28, activation='sigmoid')(d) decoded = Reshape((28, 28, 1))(d) Наконец, используя этот граф, формируем кодер, декодер и вариационный автоэнкодер: encoder = keras.Model(input_img, h, name='encoder') decoder = keras.Model(input_dec, decoded, name='decoder') vae = keras.Model(input_img, decoder(encoder(input_img)), name="vae") Все, архитектура сети задана. Теперь нам нужно определить критерий качества ее работы. Сделаем это с помощью следующей функции: def vae_loss(x, y): x = K.reshape(x, shape=(batch_size, 28*28)) y = K.reshape(y, shape=(batch_size, 28*28)) loss = K.sum(K.square(x-y), axis=-1) kl_loss = -0.5 * K.sum(1 + z_log_var - K.square(z_mean) - K.exp(z_log_var), axis=-1) return loss + kl_loss Здесь x – тензор входных данных; y – тензор выходных данных. Для удобства мы преобразовываем их в двумерные тензоры размерностью (batch_size, 28*28). И, затем, вычисляем первый критерий – сумму квадратов ошибок между входным и выходным сигналами. Причем, сумму вычисляем по последней размерности, то есть, по 28*28=784 – пикселам изображений:
Далее, идет вычисление второго критерия – расстояния Кульбака-Лейблера по тензорам z_mean и z_log_var. Чтобы лучше понять как работает эта строчка, положим, что величины z_mean и z_log_var – это векторы длиной k элементов:
И нам нужно получить формулу:
Распишем каждое из слагаемых (применительно к нашему случаю независимых СВ):
Значит, мы можем взять оценки векторов z_mean и z_log_var и записать все в таком виде: kl_loss = -0.5 * K.sum(1 + z_log_var - K.square(z_mean) - K.exp(z_log_var), axis=-1) Здесь суммирование будет происходить по длине векторов z_mean и z_log_var, то есть, k раз. В итоге получится следующий вектор:
Суммируем элементы этого вектора, умножаем на -0,5, получаем расстояние Кульбака-Лейблера:
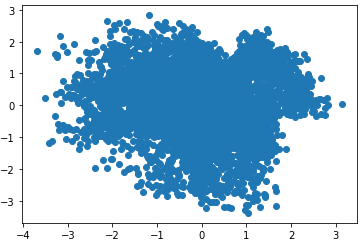
Наконец, в функции вычисления потерь, оба критерия складываются и получается единый показатель качества работы сети. Далее, мы передаем ссылку на эту функцию при компиляции вариационного автоэнкодера: vae.compile(optimizer='adam', loss=vae_loss) и запускаем процесс обучения: vae.fit(x_train, x_train, epochs=5, batch_size=batch_size, shuffle=True) Давайте посмотрим на распределение вектора скрытого состояния h: h = encoder.predict(x_test[:6000], batch_size=batch_size) plt.scatter(h[:, 0], h[:, 1])
Как видите, распределение получилось близкое к требуемому. Теперь, мы можем брать любые точки из этого пространства и должны при этом получать осмысленные изображения. Проверим это. В квадрате (-3;3) возьмем равномерно точки и подадим на вход декодера: n = 5 total = 2*n+1 plt.figure(figsize=(total, total)) num = 1 for i in range(-n, n+1): for j in range(-n, n+1): ax = plt.subplot(total, total, num) num += 1 img = decoder.predict(np.expand_dims([3*i/n, 3*j/n], axis=0)) plt.imshow(img.squeeze(), cmap='gray') ax.get_xaxis().set_visible(False) ax.get_yaxis().set_visible(False) Увидим следующий набор изображений:
В верхнем левом углу образы получились не очень понятные. Это вполне возможно, так как в точке (-3; -3) имеем самый край области и там могут быть неопределенные изображения. Также видим, что цифры 2, 4, 5, 6 представлены очень плохо. Но это, скорее, ограниченность размера скрытого пространства – всего две величины. Если увеличить его, то можно получить куда более лучшие результаты. И на следующем занятии мы это сделаем. Курс по нейронным сетям: https://stepik.org/a/227582 Видео по теме |