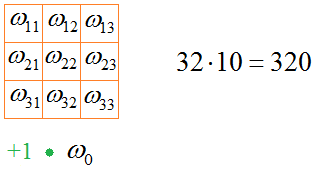|
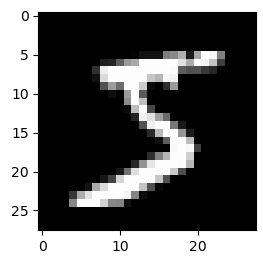
Делаем сверточную нейронную сеть в KerasКурс по нейронным сетям: https://stepik.org/a/227582 На предыдущем занятии мы с вами познакомились с общей архитектурой СНС. Как правило, они относятся к глубоким НС, то есть, с большим числом слоев. Давайте теперь посмотрим, как можно реализовать такую сеть на Keras для задачи распознавания рукописных цифр. Начнем с того, что сверточный слой в двумерном случае реализуется с помощью класса: keras.layers.Conv2D(filters, kernel_size, strides=(1, 1), …) Здесь первый параметр определяет число фильтров (каналов), а второй – размер ядра каждого фильтра. Параметр strides задает шаг сканирования фильтров по осям плоскости (по умолчанию один пиксел). Есть и другие необязательные параметры, которые мы рассмотрим выборочно. Для их полного ознакомления, можно обратиться к документации на русском языке: https://ru-keras.com/convolutional-layers/ Итак, в нашей задаче каждая рукописная цифра представлена в виде изображения 28х28 пикселей в градациях серого:
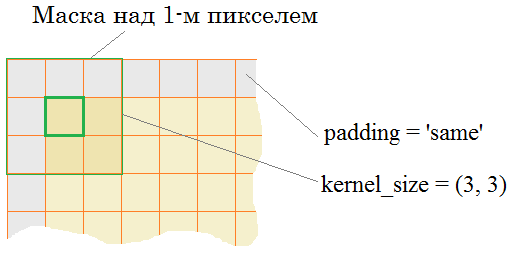
Поэтому первый сверточный слой мы определим так: model = keras.Sequential([ Conv2D(32, (3,3), padding='same', activation='relu', input_shape=(28, 28, 1)), … ]) Здесь указано 32 фильтра с ядрами 3х3 пиксела каждый. Затем, параметр padding=’same’ означает, что выходная карта признаков на каждом канале должна быть той же размерностью, что и исходное изображение, т.е. 28х28 элементов. Фактически, это означает добавление значений на границах двумерных данных (обчно нулей), чтобы центр ядра фильтра мог размещаться над граничными элементами:
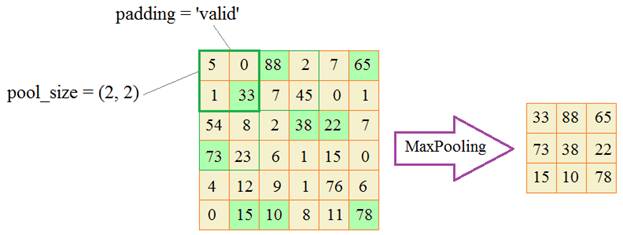
Последние два параметра вам уже знакомы: функция активации ReLu и формат входных данных в виде изображений 28х28 пикселей с одним цветовым каналом (градации серого). Следующий слой в соответствии с концепцией СНС должен укрупнять масштаб полученных признаков. Как мы говорили на предыдущем занятии, для этого чаще всего используется операция MaxPooling: keras.layers.MaxPooling2D(pool_size=(2, 2), strides=None, padding=’valid’, data_format=None) Здесь pool_size – размер окна, в котором выбирается максимальное значение; strides – шаг сканирования по координатам плоскости; padding=’valid’ – не добавлять нулевых значений на границах (соответственно рамка не смещается за пределы поля признаков); data_format – формат входных данных (об этом поговорим чуть позже).
Добавим в нашу модель операцию (слой) MaxPooling2D: model = keras.Sequential([ Conv2D(32, (3,3), padding='same', activation='relu', input_shape=(28, 28, 1)), MaxPooling2D((2, 2), strides=2), … ]) По аналогии пропишем еще два таких слоя: model = keras.Sequential([ Conv2D(32, (3,3), padding='same', activation='relu', input_shape=(28, 28, 1)), MaxPooling2D((2, 2), strides=2), Conv2D(64, (3,3), padding='same', activation='relu'), MaxPooling2D((2, 2), strides=2), … ]) Здесь следующий слой свертки содержит уже 64 фильтра, то есть, на выходе будем иметь 64 канала. После операции MaxPooling2D каждая карта признаков уменьшается до размера 7х7 элементов. Отлично, все свертки сделаны. Далее, нам нужно вытянуть полученный тензор 7х7х64 в единый вектор. Это выполняется с помощью специального слоя: keras.layers.Flatten(data_format=None) И, затем, подать его на полносвязную сеть из 128 нейронов и 10 нейронов выходного слоя. Получаем следующую архитектуру СНС для распознавания рукописных цифр: model = keras.Sequential([ Conv2D(32, (3,3), padding='same', activation='relu', input_shape=(28, 28, 1)), MaxPooling2D((2, 2), strides=2), Conv2D(64, (3,3), padding='same', activation='relu'), MaxPooling2D((2, 2), strides=2), Flatten(), Dense(128, activation='relu'), Dense(10, activation='softmax') ]) Давайте выведем структуру этой сети и посмотрим на число весовых коэффициентов в каждом слое: print(model.summary())
Смотрите, первый слой содержит 320 параметров, второй – 18496, следующий слой полносвязной НС – 401536 и последний – 1290. Почему получаются такие величины? В первом слое у нас 32 фильтра и каждый имеет 10 весовых коэффициентов, всего 320 параметров:
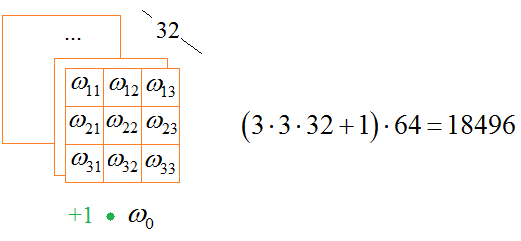
На вход следующего слоя подается 32-канальный тензор. Он обрабатывается 64 различными фильтрами. Каждый фильтр состоит из ядра 3х3х10 плюс смещение, то есть, всего имеем:
На следующий полносвязный слой подается тензор 7х7х64, вытянутый в вектор, то есть, имеем:
нейронов (плюс один биас). Все эти нейроны соединены со всеми 128 нейронами следующего слоя. Получаем число связей:
И, аналогично для последнего слоя. Здесь 128 нейронов плюс биас: 128 + 1 = 129 связаны со всеми 10 выходными нейронами:
Давайте теперь обучим эту сеть и посмотрим на результаты ее работы. Вначале подключим необходимые библиотеки, загрузим обучающую и тестовую выборки и стандартизируем входные данные: import numpy as np import matplotlib.pyplot as plt from tensorflow.keras.datasets import mnist # библиотека базы выборок Mnist from tensorflow import keras from tensorflow.keras.layers import Dense, Flatten, Dropout, Conv2D, MaxPooling2D (x_train, y_train), (x_test, y_test) = mnist.load_data() # стандартизация входных данных x_train = x_train / 255 x_test = x_test / 255 y_train_cat = keras.utils.to_categorical(y_train, 10) y_test_cat = keras.utils.to_categorical(y_test, 10) Все эти операции вам должны быть уже знакомы, так как мы их уже рассматривали на занятии распознавания цифр с помощью полносвязной НС. Но для сверточной НС множества x_tarin и x_test нужно дополнительно подготовить. Дело в том, что на входе такой сети ожидается четырехмерный тензор в формате:
Здесь channels – это каналы на входах сверточных слоев, а параметр data_format по умолчанию равен 'channels_last', что нас вполне устраивает. То есть, наши входные данные должны иметь размерность: (batch, rows = 28, cols = 28, channels = 1) Но, сейчас они представлены в виде трехмерного тензора: (batch, rows = 28, cols = 28) Нужно к ним добавить еще одно измерение (одну ось) для цветовой компоненты (одноканального изображения). Удобнее всего это сделать с помощью метода expand_dims пакета numpy: x_train = np.expand_dims(x_train, axis=3) x_test = np.expand_dims(x_test, axis=3) print( x_train.shape ) Теперь входные размерности наших данных соответствуют модели НС. Параметры компиляции и обучения мы определим стандартным образом: model.compile(optimizer='adam', loss='categorical_crossentropy', metrics=['accuracy']) his = model.fit(x_train, y_train_cat, batch_size=32, epochs=5, validation_split=0.2) И запустим процесс обучения. Точность классификации для обучающего множества и валидации составила 99% Это выше значения 97%, которое нами было ранее получено для полносвязной НС. Давайте проверим точность на тестовом множестве: model.evaluate(x_test, y_test_cat) Здесь тоже имеем значение 99%. Определенно, СНС дает лучшие результаты, чем простая полносвязная сеть при классификации изображений. И это не удивительно, хотя бы потому, что число настраиваемых параметров (весовых коэффициентов) стало больше, чем в ранее рассмотренной полносвязной НС. Кроме того, сама структура сети адаптирована именно для анализа пространственных особенностей изображения и каждый сверточный слой выполняет свою понятную функцию, обобщая пространственные признаки. Для примера, я визуализировал весовые коэффициенты для каждого отдельного сверточного слоя, правда изменил модель и взял фильтры с ядрами 8х8, чтобы лучше было видно, что они описывают. После одной эпохи обучения на первом слое получились вот такие коэффициенты:
А на следующем (после усреднения по глубине канала) по вот такие:
В целом мы здесь видим вполне осмысленные формы с некоторым обобщением на следующем уровне. Хотя, вот эти коэффициенты было бы правильно свернуть с коэффициентами предыдущего слоя, чтобы увидеть общий выходной результат. Но и эти изображения дают некоторое представление о принципе работы СНС. В пакете Keras можно найти слои: Conv1D, Conv2D, Conv3D так как на практике используют свертки для анализа одномерного, двумерного и трехмерного сигналов. Например, для:
Есть и другие виды сверток, о которых можно почитать на странице документации (некоторые из них мы будем использовать на последующих занятиях): https://ru-keras.com/convolutional-layers/ Все они работают по похожему принципу. Поэтому, если перед вами стоит задача обработки пространственных данных с помощью НС, то лучшим выбором считается сверточная архитектура. А далее, нужно определиться с числом слоев, фильтров, размеров ядер и прочих внешних параметров сети. На данный момент все это подбирается с позиции здравого смысла и опыта разработчика, а также с учетом опыта ранее созданных СНС, используемых при решении похожих задач. Курс по нейронным сетям: https://stepik.org/a/227582 Видео по теме |