|
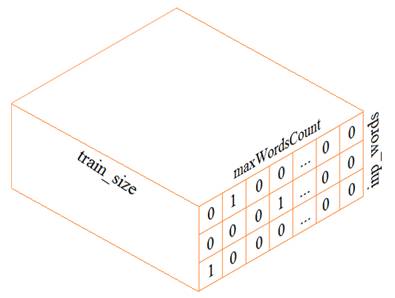
Делаем прогноз слов рекуррентной сетью Embedding слойКурс по нейронным сетям: https://stepik.org/a/227582 На предыдущем занятии мы с вами построили экспериментальную рекуррентную НС для прогнозирования следующего символа. На этом занятии разовьем эту тему и построим сеть для оценки следующего слова. В целом, сеть будет реализована также как и ранее, а вот подготовка обучающей выборки будет выполняться несколько иначе. В самом простом варианте, нам следует сформировать трехмерный тензор (похожий на тензор из предыдущего занятия):
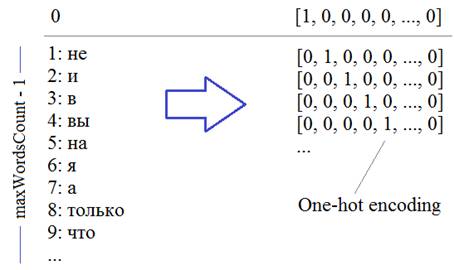
Из текста будем выделять слова целиком (а не отдельные символы, как ранее). Набор уникальных слов будут составлять наш словарь. Размер этого словаря обозначим через переменную maxWordsCount Каждое слово, затем, будет кодироваться one-hot вектором в соответствии с его номером в словаре:
Второй важный параметр – число слов, на основе которых строится прогноз, который определяется переменной: inp_words Давайте теперь посмотрим, как можно сформировать такой тензор. Вначале загрузим тексты с отрицательными высказываниями из файла text: with open('text', 'r', encoding='utf-8') as f: texts = f.read() texts = texts.replace('\ufeff', '') # убираем первый невидимый символ Теперь нам нужно разбить эти высказывания на слова. Для этого воспользуемся уже знакомым из прошлого занятия инструментом Tokenizer и положим, что максимальное число слов будет равно 1000: maxWordsCount = 1000 tokenizer = Tokenizer(num_words=maxWordsCount, filters='!–"—#$%&()*+,-./:;<=>?@[\\]^_`{|}~\t\n\r«»', lower=True, split=' ', char_level=False) tokenizer.fit_on_texts([texts]) По идее, мы здесь могли бы и не задавать максимальное число слов, тогда эта величина была бы определена автоматически при парсинге текста. Но данный параметр имеет один существенный плюс: из всех найденных слов мы оставляем 999 наиболее часто встречаемых (то есть maxWordsCount-1), то есть, мы имеем возможность отбросить редкие слова, которые особо не нужны при обучении НС. Конечно, в данном случае, останутся все найденные слова, т.к. их общее число меньше 1000. Вообще, этот параметр устанавливается с позиции «здравого смысла». Например, при большой обучающей выборке, скорее всего, мы будем иметь дело с большинством слов (и их форм) русского языка. Какой лексический запас слов у среднестатистического человека? Около 10 000. Значит, для большой выборки можно указать значение maxWordsCount = 20000 и это будет хорошим выбором. Итак, мы разбили текст на слова и для примера выведем их начальный список: dist = list(tokenizer.word_counts.items()) print(dist[:10]) Здесь отображаются кортежи со словом и его частотой встречаемости в тексте. Далее, мы преобразуем текст в последовательность чисел в соответствии с полученным словарем. Для этого используется специальный метод класса Tokenizer: data = tokenizer.texts_to_sequences([texts]) На выходе получим массив чисел объекта numpy:
Осталось закодировать числа массива data в one-hot векторы. Для этого мы воспользуемся методом to_categorical пакета Keras: res = to_categorical(data[0], num_classes=maxWordsCount) print( res.shape ) На выходе получим двумерную матрицу, состоящую из One-hot векторов:
Затем, из этой матрицы сформируем тензор обучающей выборки и соответствующий набор выходных значений. Для начала вычислим размер обучающего множества: inp_words = 3 n = res.shape[0]-inp_words И, далее, сформируем входной тензор и прогнозные значения также, как мы это делали с символами: X = np.array([res[i:i+inp_words, :] for i in range(n)]) Y = res[inp_words:] Все, у нас есть обучающая выборка и требуемые выходные значения. Осталось создать модель рекуррентной сети. Мы ее возьмем из предыдущего занятия с числом нейронов скрытого слоя 128 и maxWordsCount нейронами на выходе с функцией активации softmax: model = Sequential() model.add(Input((inp_words, maxWordsCount))) model.add(SimpleRNN(128, activation='tanh')) model.add(Dense(maxWordsCount, activation='softmax')) model.summary() model.compile(loss='categorical_crossentropy', metrics=['accuracy'], optimizer='adam') Готово. Запускаем процесс обучения: history = model.fit(X, Y, batch_size=32, epochs=50) И давайте теперь посмотрим, что у нас получилось. Запишем функцию для формирования текста из спрогнозированных слов: def buildPhrase(texts, str_len = 20): res = texts data = tokenizer.texts_to_sequences([texts])[0] for i in range(str_len): x = to_categorical(data[i: i+inp_words], num_classes=maxWordsCount) # преобразуем в One-Hot-encoding inp = x.reshape(1, inp_words, maxWordsCount) pred = model.predict( inp ) # предсказываем OHE четвертого символа indx = pred.argmax(axis=1)[0] data.append(indx) res += " " + tokenizer.index_word[indx] # дописываем строку return res И вызовем ее с тремя первыми словами: res = buildPhrase("позитив добавляет годы") print(res) Получим вот такой результат: позитив добавляет годы счастье вашей жизни и двигаться их в вы держись в и мечты успеха свою жизни не меня за не в Конечно, немного сумбурно, но в целом, что-то в этом есть. Такой результат еще связан с очень маленькой обучающей выборкой. По идее, здесь нужно взять какую-нибудь большую книгу и прогнать ее через сеть. Но цель этого занятия показать общий принцип использования рекуррентных сетей для прогнозирования слов в последовательности. Embedding-слойОднако в такой реализации есть один существенный недостаток: входной тензор, что мы получили, занимает в памяти очень много места. Представьте, если решается реальная задача с числом слов 20 000. Тогда тензора будет содержать:
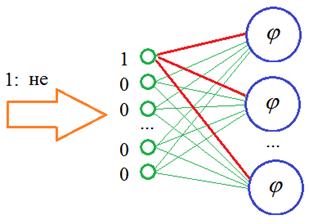
и требовать значительный объем памяти. Поэтому специалисты по нейронным сетям предложили альтернативный подход – использование специального входного слоя, который получил название: Embedding В чем его суть? Смотрите, когда мы подаем вектор с единицей на определенной позиции, то у нас, фактически, используются только связи для этого одного входа, остальные умножаются на 0 и формируют нулевые суммы на всех остальных нейронах скрытого слоя:
И отсюда хорошо видно, что если передавать на вход не такие расширенные векторы, а последовательность с порядковыми номерами слов в словаре:
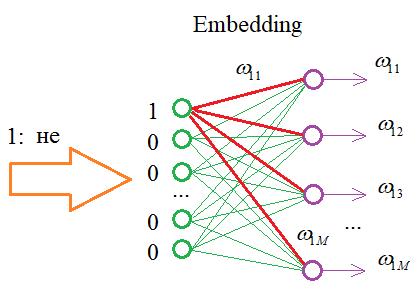
То на входе НС можно реализовать простой алгоритм, который бы подавал 1 на нейрон с соответствующим номером этого слова, а остальные суммы приравнивались бы нулю. В итоге, мы существенно экономим память при хранении обучающей выборки, а результат получаем тот же самый. Именно такую операцию и выполняет Embedding слой. На выходах его слоя формируются выходные значения, равные весам связей для переданной 1:
Далее, эти значения весов подаются уже на следующий слой нейронной сети. В Keras такой слой можно создать с помощью одноименного класса: keras.layers.Embedding(input_dim, output_dim, …, input_length)
Есть и другие параметры, подробно о них можно почитать на странице документации по ссылке: https://ru-keras.com/embedding-layers/ Этот слой можно создавать только как входной и в нашем случае мы его определим так: model.add(Embedding(maxWordsCount, 256, input_length = inp_words)) Здесь 256 – это число выходов в Embedding-слое. В качестве входной обучающей выборки мы теперь можем использовать одномерный массив: data = tokenizer.texts_to_sequences([texts]) res = np.array( data[0] ) print( res.shape ) inp_words = 3 n = res.shape[0]-inp_words X = np.array([res[i:i+inp_words] for i in range(n)]) Y = to_categorical(res[inp_words:], num_classes=maxWordsCount) А выходные значения остаются прежними – двумерным массивом из One-hot векторов, так как у нас на выходе 1000 нейронов. Далее, абсолютно также проводим обучение и немного модифицируем функцию buildPhrase: x = data[i: i+inp_words] inp = np.expand_dims(x, axis=0) И запускаем процесс прогнозирования слов. Как видите, использование Embedding слоя значительно упрощает и саму программу и размер используемой памяти. Курс по нейронным сетям: https://stepik.org/a/227582 Видео по теме |