|
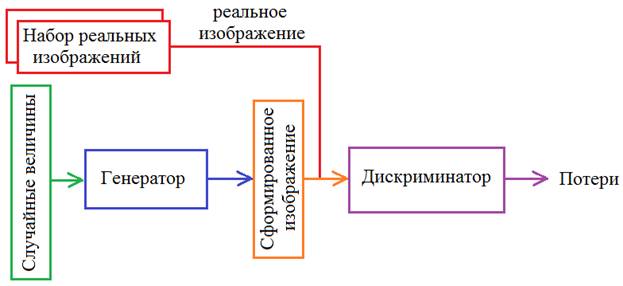
Делаем генеративно-состязательную сеть в Keras и TensorflowКурс по нейронным сетям: https://stepik.org/a/227582 На предыдущем занятии мы с вами рассмотрели общую концепцию генеративно-состязательных сетей. Теперь, пришло время ее реализовать. Для этого мы воспользуемся пакетом Keras и кое-что сделаем непосредственно через Tensorflow, в частности, раздельный процесс обучения генератора и дискриминатора. Итак, общая схема генеративно-состязательной сети, будет следующей:
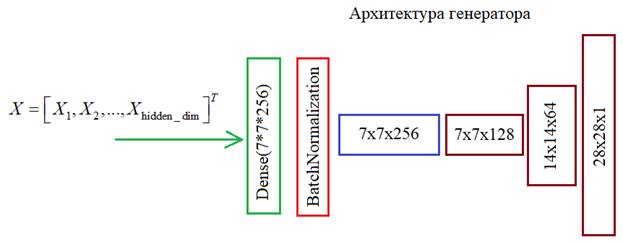
Чтобы генератор лучше формировал изображения, их следует взять однотипными. Например, из базы MNIST выбрать только семерки: import numpy as np import matplotlib.pyplot as plt import time from tensorflow.keras.datasets import mnist from tensorflow import keras import keras.backend as K import tensorflow as tf from tensorflow.keras.layers import Dense, Flatten, Reshape, Input, BatchNormalization, Dropout from tensorflow.keras.layers import Conv2D, Conv2DTranspose, LeakyReLU (x_train, y_train), (x_test, y_test) = mnist.load_data() x_train = x_train[y_train==7] y_train = y_train[y_train==7] Затем, определим две константы: BUFFER_SIZE = x_train.shape[0] BATCH_SIZE = 100 и сделаем общую выборку кратную величине BATCH_SIZE: BUFFER_SIZE = BUFFER_SIZE // BATCH_SIZE * BATCH_SIZE x_train = x_train[:BUFFER_SIZE] y_train = y_train[:BUFFER_SIZE] print(x_train.shape, y_train.shape) Стандартизируем входные данные: x_train = x_train / 255 x_train = np.reshape(x_train, (len(x_train), 28, 28, 1)) И из них формируем тензор реальных изображений, разбитых по батчам: train_dataset = tf.data.Dataset.from_tensor_slices(x_train).shuffle(BUFFER_SIZE).batch(BATCH_SIZE) Обучающая выборка готова. Далее, определим две сети: генератор и дискриминатор. Сделаем их на базе сверточных слоев, так как мы работаем с изображениями, а для них хорошо себя зарекомендовали именно такие сети. Сеть генератора будет следующей: # формирование сетей hidden_dim = 2 def dropout_and_batch(): return Dropout(0.3)(BatchNormalization()) # генератор generator = tf.keras.Sequential([ Dense(7*7*256, activation='relu', input_shape=(hidden_dim,)), BatchNormalization(), Reshape((7, 7, 256)), Conv2DTranspose(128, (5, 5), strides=(1, 1), padding='same', activation='relu'), BatchNormalization(), Conv2DTranspose(64, (5, 5), strides=(2, 2), padding='same', activation='relu'), BatchNormalization(), Conv2DTranspose(1, (5, 5), strides=(2, 2), padding='same', activation='sigmoid'), ])
Генератор на вход будет получать вектор независимых нормальных СВ, размерностью hidden_dim:
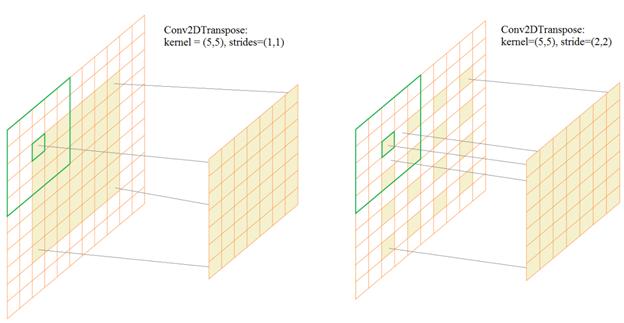
Затем, с помощью слоя Dense он масштабируется до размера 7*7*256 элементов и в слое Reshape преобразуется в тензор с размерами: 7х7х256 Далее, выполняется операция транспонированной свертки Conv2DTranspose. Принцип ее работы прост и лучше всего виден вот на этом анимированном рисунке conv2dtranspose - (3,3), (2,2).gif В частности, у нас происходит следующее. Сначала тензор 7х7х256 преобразуется слоем Conv2DTranspose с ядром 5х5 элементов и шагом (1, 1). На выходе получим те же размеры 7х7, но 128 каналов. Следующий слой Conv2DTranspose имеет ядро 5х5 и шаг (2, 2). Это означает, что входные значения размером 7х7 каждого канала располагаются через отсчет и по ним скользит маска размером 5х5, причем маска смещается на один отсчет. В результате, на выходе получаем размер карт признаков 14х14.
Затем, операция повторяется, также увеличивая размер выходного канала в 2 раза до 28х28. Это и будет результатом работы генератора, то есть, выходное изображение. Следом определяем сеть дискриминатора: # дискриминатор discriminator = tf.keras.Sequential() discriminator.add(Conv2D(64, (5, 5), strides=(2, 2), padding='same', input_shape=[28, 28, 1])) discriminator.add(LeakyReLU()) discriminator.add(Dropout(0.3)) discriminator.add(Conv2D(128, (5, 5), strides=(2, 2), padding='same')) discriminator.add(LeakyReLU()) discriminator.add(Dropout(0.3)) discriminator.add(Flatten()) discriminator.add(Dense(1)) Здесь все вам уже должно быть знакомо. На входе ожидаем изображение 28х28 пикселей, а на выходе имеем один нейрон с линейной функцией активации. Такая функция выбрана не случайно. Она предотвращает попадание в области насыщения, которые имеются у других функций, например, сигмоидальной или гиперболического тангенса. Линейная функция не ограничивает выходное значение, а значит, не уменьшает результирующие градиенты. Это очень важно при обучении такой сети. Итак, Сети определены. Дальше мы объявим две функции для вычисления потерь генератора и дискриминатора: # потери cross_entropy = tf.keras.losses.BinaryCrossentropy(from_logits=True) def generator_loss(fake_output): loss = cross_entropy(tf.ones_like(fake_output), fake_output) return loss def discriminator_loss(real_output, fake_output): real_loss = cross_entropy(tf.ones_like(real_output), real_output) fake_loss = cross_entropy(tf.zeros_like(fake_output), fake_output) total_loss = real_loss + fake_loss return total_loss Мы используем встроенную
функцию BinaryCrossentropy пакета Keras для вычисления бинарной
кросс-энтропии. Далее, в функции generator_loss в бинарной
кросс-энтропии передаем два параметра: желаемый и реальный отклики. У
генератора желаемый отклик дискриминатора должен быть
По аналогии вычисляются потери для дискриминатора. Ему на вход последовательно будем подавать реальное и фейковое изображения, получать два разных отклика real_output и fake_output и на их основе вычислять потери в соответствии с формулой:
Здесь требуемые
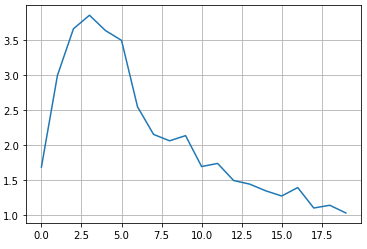
отклики равны После определения потерь, зададим оптимизаторы для алгоритма градиентного спуска по Адаму с шагом 0,0001: generator_optimizer = tf.keras.optimizers.Adam(1e-4) discriminator_optimizer = tf.keras.optimizers.Adam(1e-4) Теперь у нас все готово, чтобы сформировать процесс обучения генератора и дискриминатора. Для этого воспользуемся непосредственно средствами Tensorflow 2.0 и определим функцию одного шага обучения через декоратор tf.function: # обучение @tf.function def train_step(images): noise = tf.random.normal([BATCH_SIZE, hidden_dim]) with tf.GradientTape() as gen_tape, tf.GradientTape() as disc_tape: generated_images = generator(noise, training=True) real_output = discriminator(images, training=True) fake_output = discriminator(generated_images, training=True) gen_loss = generator_loss(fake_output) disc_loss = discriminator_loss(real_output, fake_output) gradients_of_generator = gen_tape.gradient(gen_loss, generator.trainable_variables) gradients_of_discriminator = disc_tape.gradient(disc_loss, discriminator.trainable_variables) generator_optimizer.apply_gradients(zip(gradients_of_generator, generator.trainable_variables)) discriminator_optimizer.apply_gradients(zip(gradients_of_discriminator, discriminator.trainable_variables)) return gen_loss, disc_loss Давайте разберемся что здесь происходит. На вход функции подаем пакет (батч) реальных изображений. Затем, формируем также один батч вектор нормальных случайных величин длиной hidden_dim. Их мы подаем на вход генератора. Так как нам будут нужны градиенты для сети генератора и дискриминатора, то мы их вычислим с помощью инструмента Tensorflow GradientTape. Он сохраняет необходимые результаты арифметических операции для дальнейшего вычисления градиентов. Это довольно продвинутый инструмент автоматического дифференцирования, о котором можно посмотреть на странице официальной документации: https://www.tensorflow.org/guide/autodiff Я не буду на нем подробно останавливаться, чтобы не перегружать материал, нам здесь важно лишь знать, что объекты gen_tape и disc_tape будут содержать необходимые данные для последующего вычисления градиентов изменяемых параметров (то есть, весов сетей) в точках, соответствующих входным данным. Благодаря тесной интеграции пакета Keras и Tensorflow, при прохождении сигнала по генератору и дискриминатору: real_output = discriminator(images, training=True) fake_output = discriminator(generated_images, training=True) в объекты gen_tape и disc_tape автоматически записываются необходимые данные. То же самое происходит и при вычислении потерь для обеих сетей. Теперь, все что нам нужно для вычисления градиентов, это вызвать метод gradient объектов gen_tape и disc_tape. В качестве первого параметра указываем целевую функцию, то есть, функцию потерь, а вторым параметром – оптимизируемые аргументы, от которых зависит эта целевая функция. Конечно, аргументы здесь – это веса соответствующих сетей. После вычисления градиентов, мы их применяем для изменения весов, используя метод apply_gradients объекта оптимизатора. В качестве параметра передаем список градиентов и оптимизируемых весовых коэффициентов. Это и есть момент обучения сети. Делаем это независимо для генератора и дискриминатора. В конце, возвращаем значения потерь для генератора и дискриминатора. Это функция для выполнения одного шага обучения по батчу. Теперь, объявим функцию, которая будет запускать весь процесс обучения сетей. На ее вход будем передавать обучаемую выборку изображений, разбитой по батчам и число эпох: def train(dataset, epochs): history = [] MAX_PRINT_LABEL = 10 th = BUFFER_SIZE // (BATCH_SIZE*MAX_PRINT_LABEL) for epoch in range(1, epochs+1): print(f'{epoch}/{EPOCHS}: ', end='') start = time.time() n = 0 gen_loss_epoch = 0 for image_batch in dataset: gen_loss, disc_loss = train_step(image_batch) gen_loss_epoch += K.mean(gen_loss) if( n % th == 0): print('=', end='') n += 1 history += [gen_loss_epoch/n] print(': '+str(history[-1])) print ('Время эпохи {} составляет {} секунд'.format(epoch + 1, time.time()-start)) return history Здесь все достаточно просто. Вначале определяем вспомогательные переменные. И, затем, делаем цикл по эпохам. Для каждой эпохи замеряем время ее выполнения и запускаем цикл обучения по батчам, вызывая функцию train_step. Далее, вычисляем средние потери для генератора по батчам и выводим результат в консоль, а также сохраняем в коллекции history. В конце возвращаем историю изменения потерь для генератора. Наконец, запускаем процесс обучения и отображаем график изменения потерь для генератора по эпохам: # запуск процесса обучения EPOCHS = 20 history = train(train_dataset, EPOCHS) plt.plot(history) plt.grid(True)
Смотрите, здесь наблюдается некоторый колебательный процесс. И это естественно. Сначала происходит резкое увеличение потерь из-за преимущественного обучения дискриминатора (он учится отличать реальные изображения от фейковых). Затем, немного обучившись, градиенты для генератора стали больше градиентов дискриминатора и потери генератора стали уменьшаться (изображения на его выходе становятся реалистичнее). Далее, опять видим небольшие всплески – это моменты улучшения дискриминатора и в целом все это доходит до некоторого равновесного состояния. В идеале, генератор должен выдавать изображения неотличимые от реальных и дискриминатор с вероятностью 0,5 может их различать, то есть, не различать вовсе. Давайте теперь посмотрим, что выдает генератор после 20 эпох обучения: # отображение результатов генерации n = 2 total = 2*n+1 plt.figure(figsize=(total, total)) num = 1 for i in range(-n, n+1): for j in range(-n, n+1): ax = plt.subplot(total, total, num) num += 1 img = generator.predict(np.expand_dims([0.5*i/n, 0.5*j/n], axis=0)) plt.imshow(img[0,:,:,0], cmap='gray') ax.get_xaxis().set_visible(False) ax.get_yaxis().set_visible(False)
Как видим, получаются вполне четкие не смазанные изображения семерок. Это как раз то, к чему мы стремились. Теперь, обученный генератор можно использовать отдельно для формирования таких изображений. Генеративно-состязательные сети, как правило, долго обучаются в сравнении с обычными сетями. Здесь нам приходится подстраивать весовые коэффициенты отдельно для дискриминатора, затем для генератора и это конкурирующее обучение необходимо повторять много раз для достижения приемлемых результатов. Поэтому число эпох может достигать 100 и более. Дополнительные сложности при обучении возникают из-за взаимного влияния дискриминатора и генератора друг на друга. Вполне может возникнуть ситуация, когда градиенты генератора будут близки к нулю и обучение попадает в некую ловушку, когда недообученный дискриминатор хорошо различает фейковые изображения недообученного генератора. При этом, генератор дальше не обучается из-за этих малых градиентов. Но все это можно преодолеть при грамотном подходе к обучению. Вот так можно в самом простом случае реализовать и обучить генеративно-состязательную сеть для формирования реалистичных изображений цифр. Курс по нейронным сетям: https://stepik.org/a/227582 Видео по теме |