|
Двунаправленные (bidirectional) рекуррентные нейронные сетиВсе ранее рассмотренные архитектуры рекуррентных НС были однонаправленными: они обрабатывали входной сигнал последовательно во времени:
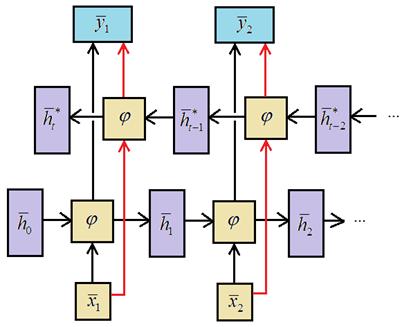
Но иногда лучше проводить обработку и в прямом и в обратном направлениях одновременно. Например, мы хотим спрогнозировать недостающее слово по его окружающему контексту: Уже сейчас искусственный интеллект завоевывает самые разные прикладные области Для этого нужно знать и прошлый и будущий контекст. Как раз для такого рода задач и были предложены двунаправленные рекуррентные НС. В целом, их архитектура достаточно проста и представлена двумя рекуррентными слоями, разворачивающихся в противоположных направлениях:
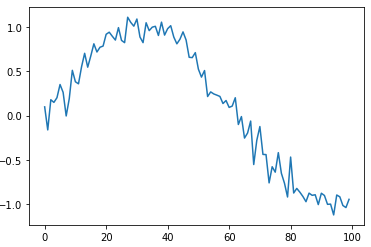
Давайте реализуем такую сеть с использованием блоков GPU. Чтобы обычный рекуррентный слой превратить в двунаправленный в Keras используется специальный класс: keras.layers.Bidirectional(…) В качестве первого аргумента здесь указывается слой, который следует превратить в двунаправленный, например, так: model.add( Bidirectional(GRU(64)) ) В качестве практической реализации мы рассмотрим задачу регрессии. Предположим, что имеется синусоида с добавленным к ней шумом: N = 10000 data = np.array([np.sin(x/20) for x in range(N)]) + 0.1*np.random.randn(N) plt.plot(data[:100])
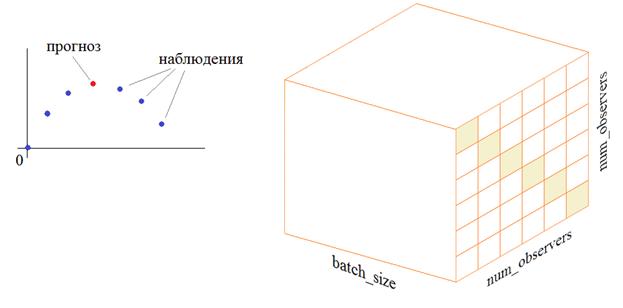
И далее, мы собираемся строить прогноз отдельных отсчетов этой кривой, следующим образом:
То есть, брать три предыдущих и три следующих наблюдения относительно прогнозируемого значения. Чтобы рекуррентная НС могла корректно обрабатывать последовательность наблюдений, представим их в виде трехмерного тензора, где по главной диагонали будут записаны значения наблюдений для текущего временного среза. Такая модель входных данных позволит сети с 6 входами «понимать» местоположение каждого наблюдения относительно оцениваемого элемента. Формирование входного тензора и контролируемых выходных значений, делают следующие строчки программы: off = 3 length = off*2+1 X = np.array([ np.diag(np.hstack((data[i:i+off], data[i+off+1:i+length]))) for i in range(N-length)]) Y = data[off:N-off-1] print(X.shape, Y.shape, sep='\n') Здесь off – число наблюдений до и после прогнозируемого значения; length – общее число отсчетов (вместе с прогнозируемым значением). Далее, формируется входной вектор X. Функция diag формирует диагональную матрицу из вектора, а функция hstack объединяет два вектора в один. Требуемые выходные значения Y – это просто сдвиг данных массива data на величину off. Теперь опишем модель НС: model = Sequential() model.add(Input((length-1, length-1))) model.add( Bidirectional(GRU(2)) ) model.add(Dense(1, activation='linear')) model.summary() model.compile(loss='mean_squared_error', optimizer=Adam(0.01)) Сначала идет входной слой, размером length-1, length-1 для каждого батча, то есть, на входе рекуррентной сети ожидается тензор размерностью: (batch_size, length-1, length-1) Далее, идет двунаправленный рекуррентный слой из двух нейронов в каждой ячейке GRU. На выходе сети у нас будет один нейрон с линейной функцией активации (в задачах регрессии, когда на выходе ожидается определенное число в произвольном диапазоне значений, используется именно такая функция активации). При компиляции этой модели мы указываем функцию потерь минимум среднего квадрата ошибки и оптимизацию по Адам с шагом сходимости 0,01 (одна сотая). Запускаем процесс обучения: history = model.fit(X, Y, batch_size=32, epochs=10) И посмотрим на выходные значения НС. Прогноз будем строить так:
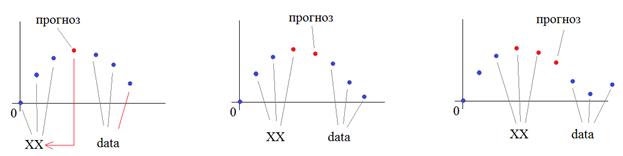
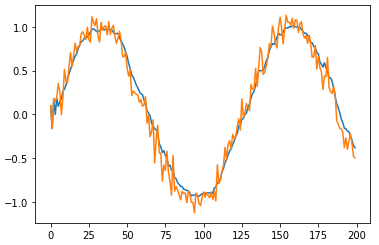
Давайте посмотрим, что в результате у нас получится: M = 200 XX = np.zeros(M) XX[:off] = data[:off] for i in range(M-off-1): x = np.diag( np.hstack( (XX[i:i+off], data[i+off+1:i+length])) ) x = np.expand_dims(x, axis=0) y = model.predict(x) XX[i+off+1] = y plt.plot(XX[:M]) plt.plot(data[:M])
Смотрите, оранжевый график – это исходный сигнал, а синий – результат прогнозирования НС. Получилась, в общем то, ожидаемая картина: произошло сглаживание входного сигнала. Именно такая процедура минимизирует среднеквадратическую ошибку. Конечно, этого же (и даже лучшего) результата легко добиться традиционными алгоритмами фильтрации. Я привел этот пример лишь для демонстрации построения двунаправленной рекуррентной сети в пакете Keras, а также для еще одного примера задачи регрессии, о которой мы давно не говорили. Надеюсь, теперь вы представляете, что из себя представляет архитектура двунаправленных рекуррентных сетей и как она реализуется в пакете Keras. Видео по теме |
