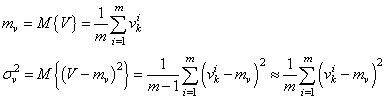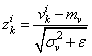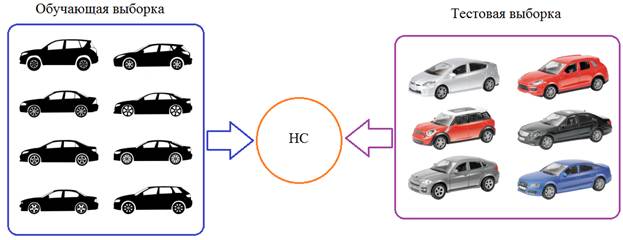
|
Batch Normalization (батч-нормализация) что это такое?Вам что-нибудь говорит термин внутренний ковариационный сдвиг: internal covariance shift Звучит очень умно, не так ли? И не удивительно. Это понятие в 2015-м году ввели два сотрудника корпорации Google: Sergey Ioffe и Christian Szegedy (Иоффе и Сегеди) решая проблему ускорения процесса обучения НС. И мы сейчас посмотрим, что же они предложили, как это работает и, наконец, что же это за ковариационный сдвиг. Как раз с последнего я и начну. Давайте предположим, что мы обучаем НС распознавать машины (неважно какие, главное чтобы сеть на выходе выдавала признак: машина или не машина). Но, при обучении мы используем автомобили только черного цвета. После этого, сеть переходит в режим эксплуатации и ей предъявляются машины уже разных цветов:
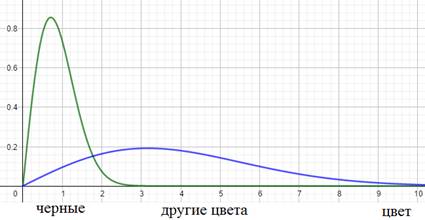
Как вы понимаете, это не лучшим образом скажется на качестве ее работы. Так вот, на языке математики этот эффект можно выразить так. Начальное распределение цветов (пусть это будут градации серого) обучающей выборки можно описать с помощью вот такой плотности распределения вероятностей (зеленый график):
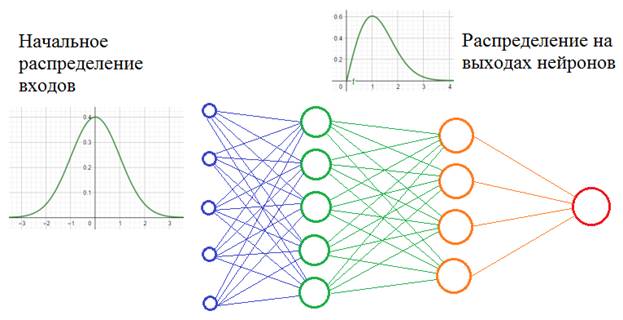
А распределение всего множества цветов машин, встречающихся в тестовой выборке в виде синего графика. Как видите эти графики имеют различные МО и дисперсии. Эта разница статистических характеристик и приводит к ковариационному сдвигу. И теперь мы понимаем: если такой сдвиг имеет место быть, то это негативно сказывается на работе НС. Но это пример внешнего ковариационного сдвига. Его легко исправить, поместив в обучающую выборку нужное количество машин с разными цветами. Есть еще внутренний ковариационный сдвиг – это когда статистическая картина меняется внутри сети от слоя к слою:
Само по себе такое изменение статистик не несет каких-либо проблем. Проблемы проявляются в процессе обучения, когда при изменении весов связей предыдущего слоя статистическое распределение выходных значений нейронов текущего слоя становится заметно другим. И этот измененный сигнал идет на вход следующего слоя. Это похоже на то, словно на вход скрытого слоя поступают то машины черного цвета, то машины красного цвета или какого другого. То есть, весовые коэффициенты в пределах мини-батча только адаптировались к черным автомобилям, как в следующем мини-батче им приходится адаптироваться к другому распределению – красным машинам и так постоянно. В ряде случаев это может существенно снижать скорость обучения и, кроме того, для адаптации в таких условиях приходится устанавливать малое значение шага сходимости, чтобы весовые коэффициенты имели возможность подстраиваться под разные статистические распределения. Это описание проблемы, которую, как раз, и выявили сотрудники Гугла, изучая особенности обучения многослойных НС. Решение кажется здесь очевидным: если проблема в изменении статистических характеристик распределения на выходах нейронов, то давайте их стандартизировать, нормализовывать – приводить к единому виду. Именно это и делается при помощи предложенного алгоритма Batch Normalization Осталось
выяснить: какие характеристики и как следует нормировать. Из теории
вероятностей мы знаем, что самые значимые из них – первые две: МО и дисперсия.
Так вот, в алгоритме batch normalization их приводят к
значениям 0 и 1, то есть, формируют распределение с нулевым МО и единичной
дисперсией. Чуть позже я подробнее поясню как это делается, а пока ответим на
второй вопрос: для каких величин и в какой момент производится эта нормировка? Разработчики
этого метода рекомендовали располагать нормировку для величин
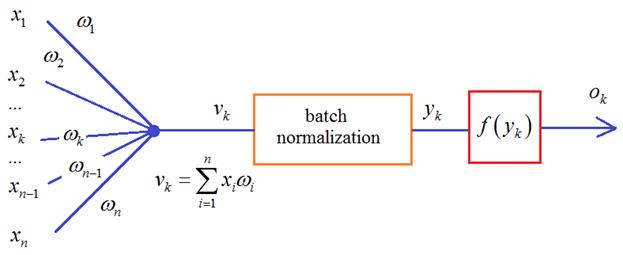
Но сейчас уже имеются результаты исследований, которые показывают, что этот блок может давать хорошие результаты и после функции активации. Что же из себя представляет batch normalization и где тут статистики? Давайте вспомним, что НС обучается пакетами наблюдений – батчами. И для каждого наблюдения из batch на входе каждого нейрона получается свое значение суммы:
Здесь m – это размер пакета, число наблюдений в батче. Так вот статистики вычисляются для величин V в пределах одного batch:
И, далее, чтобы вектор V имел нулевое среднее и единичную дисперсию, каждое значение преобразовывают по очевидной формуле:
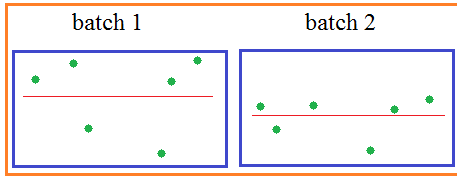
здесь
будет иметь нулевое МО и почти единичную дисперсию. Но этого недостаточно. Если оставить как есть, то будут теряться естественные статистические характеристики наблюдений между батчами: небольшие изменения в средних значениях и дисперсиях, т.е. будет уменьшена репрезентативность выборки:
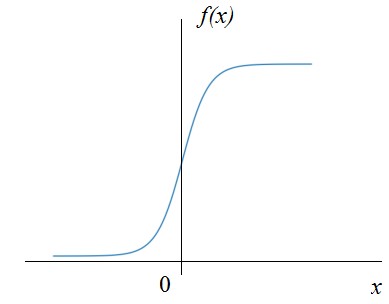
Кроме того, сигмоидальная функция активации вблизи нуля имеет практически линейную зависимость, а значит, простая нормировка значений x лишит НС ее нелинейного характера, что приведет к ухудшению ее работы:
Поэтому
нормированные величины
Параметры Далее, величина
Но это лишь возможные эффекты – они могут и не проявиться или даже, наоборот, применение этого алгоритма ухудшит обучаемость НС. Рекомендация здесь такая: Изначально строить нейронные сети без batch normalization (или dropout) и если наблюдается медленное обучение или эффект переобучения, то можно попробовать добавить batch normalization или dropout, но не оба вместе. Реализация batch normalization в KerasДавайте теперь посмотрим как можно реализовать данный алгоритм в пакете Keras. Для этого существует класс специального слоя, который так и называется: keras.layers.BatchNormalization Он применяется к выходам предыдущего слоя, после которого указан в модели НС, например: model = keras.Sequential([ Flatten(input_shape=(28, 28, 1)), Dense(300, activation='relu'), BatchNormalization(), Dense(10, activation='softmax') ]) Здесь нормализация применяется к выходам скрытого слоя, состоящего из 300 нейронов. Правда в такой простой НС нормализация, скорее, негативно сказывается на обучении. Этот метод обычно помогает при большом числе слоев, то есть, при deep learning. Видео по теме |
перед
функцией активации:
-
небольшое положительное число, исключающее деление на ноль, если дисперсия
будет близка к нулевым значениям. В итоге, вектор
дополнительно
масштабируются и смещаются в соответствии с формулой:
с
начальными значениями 1 и 0 также подбираются в процессе обучения НС с помощью
того же алгоритма градиентного спуска. То есть, у сети появляются
дополнительные настраиваемые переменные, помимо весовых коэффициентов.
подается
на вход функции активации и формируется выходное значение нейрона. Вот так
работает алгоритм batch normalization, который дает
следующие возможные эффекты:
