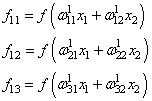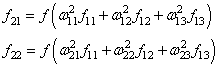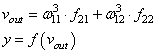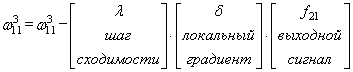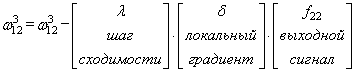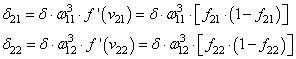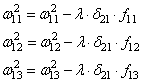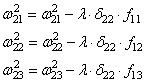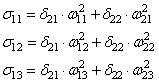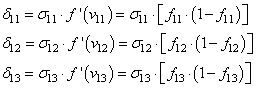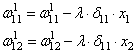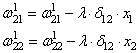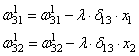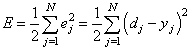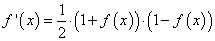|
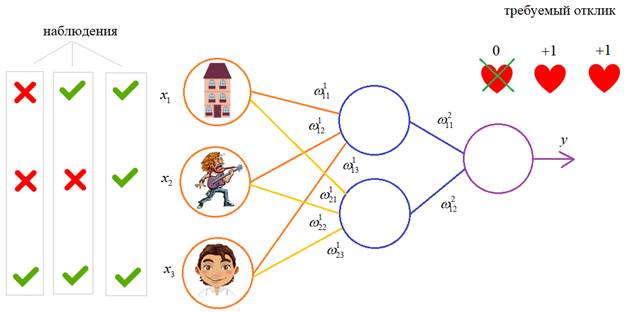
Back propagation - алгоритм обучения по методу обратного распространенияКурс по нейронным сетям: https://stepik.org/a/227582 На предыдущих занятиях мы с вами рассматривали НС с выбранными весами, либо устанавливали их, исходя из определенных математических соображений. Это можно сделать, когда сеть относительно небольшая. Но при увеличении числа нейронов и связей, ручной подбор становится попросту невозможным и возникает задача нахождения весовых коэффициентов связей НС. Этот процесс и называют обучением нейронной сети. Один из распространенных подходов к обучению заключается в последовательном предъявлении НС векторов наблюдений и последующей корректировки весовых коэффициентов так, чтобы выходное значение совпадало с требуемым:
Это называется обучение с учителем, так как для каждого вектора мы знаем нужный ответ и именно его требуем от нашей НС. Теперь, главный вопрос: как построить алгоритм, который бы наилучшим образом находил весовые коэффициенты. Наилучший – это значит, максимально быстро и с максимально близкими выходными значениями для требуемых откликов. В общем случае эта задача не решена. Нет универсального алгоритма обучения. Поэтому, лучшее, что мы можем сделать – это выбрать тот алгоритм, который хорошо себя зарекомендовал в прошлом. Основной «рабочей лошадкой» здесь является алгоритм back propagation (обратного распространения ошибки), который, в свою очередь, базируется на алгоритме градиентного спуска. Сначала, я думал рассказать о нем со всеми математическими выкладками, но потом решил этого не делать, а просто показать принцип работы и рассмотреть реализацию конкретного примера на Python. Чтобы все лучше
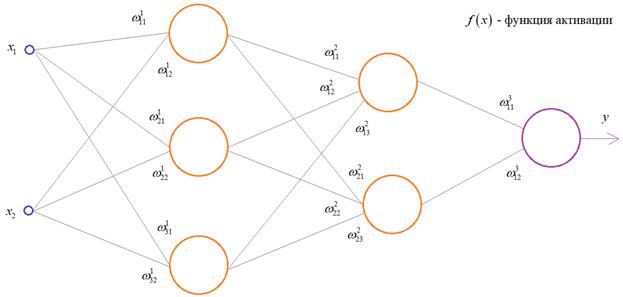
понять, предположим, что у нас имеется вот такая полносвязная НС прямого
распространения с весами связей, выбранными произвольным образом в диапазоне от
[-0.5; 0,5]. Здесь верхний индекс показывает принадлежность к тому или иному слою
сети. Также, каждый нейрон имеет некоторую активационную функцию
На первом шаге
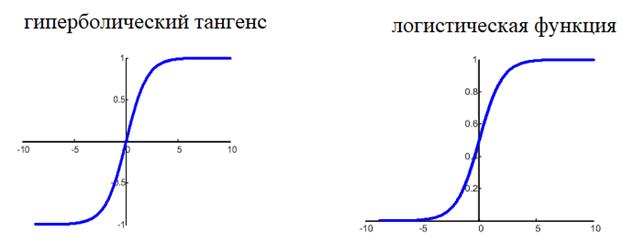
делается прямой проход по сети. Мы пропускаем вектор наблюдения
и последнее выходное значение y:
Далее, мы знаем
требуемый отклик d для текущего вектора
На данный момент все должно быть понятно. Мы на первом занятии подробно рассматривали процесс распространения сигнала по НС. И вы это уже хорошо себе представляете. А вот дальше начинается самое главное – корректировка весов. Для этого делается обратный проход по НС: от последнего слоя – к первому. Итак, у нас есть
ошибка e и некая функция
активации нейронов
Этот момент требует пояснения. Смотрите, ранее используемая пороговая функция:
нам уже не подходит, т.к. она не дифференцируема на всем диапазоне значений x. Вместо этого для сетей с небольшим числом слоев, часто применяют или гиперболический тангенс:
или логистическую функцию:
Фактически, они отличаются только тем, что первая дает выходной интервал [-1; 1], а вторая – [0; 1]. И мы уже берем ту, которая нас больше устраивает в данной конкретной ситуации. Например, выберем логистическую функцию.
Ее производная функции по аргументу x дает очень простое выражение:
Именно его мы и запишем в нашу формулу вычисления локального градиента:
Но, так как
то локальный градиент последнего нейрона, равен:
Отлично, это
сделали. Теперь у нас есть все, чтобы выполнить коррекцию весов. Начнем со
связи
Для второй связи все то же самое, только входной сигнал берется от второго нейрона:
Здесь у вас может возникнуть вопрос: что такое параметр λ и где его брать? Он подбирается самостоятельно, вручную самим разработчиком. В самом простом случае можно попробовать следующие значения:
(Мы подробно о нем говорили на занятии по алгоритму градиентного спуска): Итак, мы с вами скорректировали связи последнего слоя. Если вам все это понятно, значит, вы уже практически поняли весь алгоритм обучения, потому что дальше действуем подобным образом. Переходим к нейрону следующего с конца слоя и для его входящих связей повторим ту же саму процедуру. Но для этого, нужно знать значение его локального градиента. Определяется он просто. Локальный градиент последнего нейрона взвешивается весами входящих в него связей. Полученные значения на каждом нейроне умножаются на производную функции активации, взятую в точках входной суммы:
А дальше действуем по такой же самой схеме, корректируем входные связи по той же формуле:
И для второго нейрона:
Осталось скорректировать веса первого слоя. Снова вычисляем локальные градиенты для нейронов первого слоя, но так как каждый из них имеет два выхода, то сначала вычисляем сумму от каждого выхода:
А затем, значения локальных градиентов на нейронах первого скрытого слоя:
Ну и осталось выполнить коррекцию весов первого слоя все по той же формуле:
В результате, мы выполнили одну итерацию алгоритма обучения НС. На следующей итерации мы должны взять другой входной вектор из нашего обучающего множества. Лучше всего это сделать случайным образом, чтобы не формировались возможные ложные закономерности в последовательности данных при обучении НС. Повторяя много раз этот процесс, весовые связи будут все точнее описывать обучающую выборку. Отлично, процесс обучения в целом мы рассмотрели. Но какой критерий качества минимизировался алгоритмом градиентного спуска? В действительности, мы стремились получить минимум суммы квадратов ошибок для обучающей выборки:
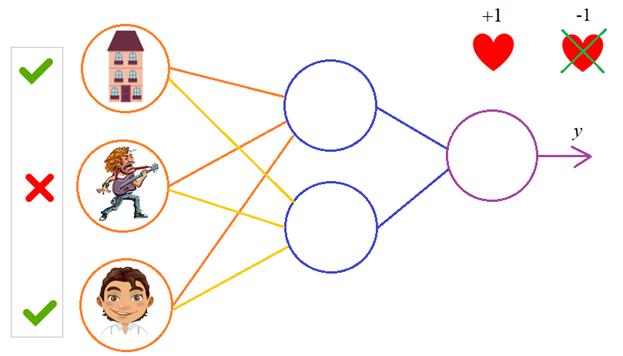
То есть, с помощью алгоритма градиентного спуска веса корректируются так, чтобы минимизировать этот критерий качества работы НС. Позже мы еще увидим, что на практике используется не только такой, но и другие критерии. Вот так, в целом выглядит идея работы алгоритма обучения по методу обратного распространения ошибки. Давайте теперь в качестве примера обучим следующую НС:
В качестве обучающего множества выберем все возможные варианты (здесь 1 – это да, -1 – это нет):
На каждой итерации работы алгоритма, мы будем подавать случайно выбранный вектор и корректировать веса, чтобы приблизиться к значению требуемого отклика. В качестве активационной функции выберем гиперболический тангенс:
со значением производной:
Программа на Python будет такой: Ну, конечно, это довольно простой, примитивный пример, частный случай, когда мы можем обучить НС так, чтобы она вообще не выдавала никаких ошибок. Часто, в задачах обучения встречаются варианты, когда мы этого сделать не можем и, конечно, какой-то процент ошибок всегда остается. И наша задача сделать так, чтобы этих ошибок было как можно меньше. Но более подробно как происходит обучение, какие нюансы существуют, как создавать обучающую выборку, как ее проверять и так далее, мы об этом подробнее будем говорить уже на следующем занятии. Курс по нейронным сетям: https://stepik.org/a/227582 Видео по теме |