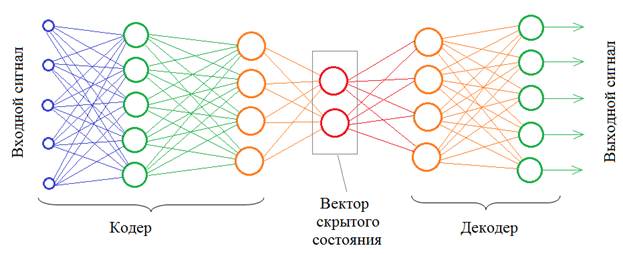
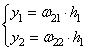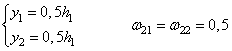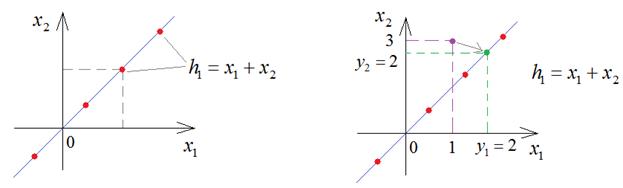Автоэнкодеры. Что это и как работаютКурс по нейронным сетям: https://stepik.org/a/227582 Теперь, когда мы с вами в целом разобрались с основными архитектурами НС и некоторыми примерами их использования, поговорим о других более продвинутых построениях и начнем с такой их разновидности как автоэнкодеры. В самом простом варианте автоэнкодер – это НС, которая сначала кодирует входной сигнал в некоторое скрытое состояние, размерность которого, как правило, меньше размерности входного сигнала, а затем, из скрытого состояния снова разворачивает (декодирует) данные в другое, новое состояние:
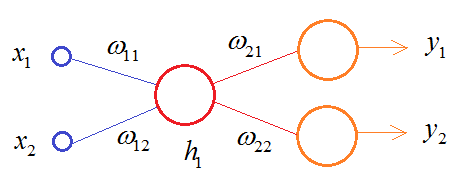
Размерности входных и выходных векторов, в общем случае, могут отличаться. Например, можно попробовать обучить автоэнкодер масштабировать изображения. В другом примере, сжатия данных, декодер должен как можно точнее воспроизвести входное изображение, опираясь только на вектор скрытого состояния. Сам же этот вектор будет представлять сжатое изображение. Правда, НС в области сжатия работают хуже традиционных алгоритмов, поэтому автоэнкодеры нашли свое применение в других областях. И некоторые из них мы с вами рассмотрим. Но сначала в целом разберемся в принципах его работы. Давайте возьмем простейший автоэнкодер с линейной функцией активации:
В этой схеме кодер выполняет очень простую операцию:
А декодер
разворачивает значение
Предположим, что
значение
Затем, декодер пытается восстановить снова эти два значения и делает это, например, следующим образом:
В результате,
получаем модель представления входных данных в скрытом состоянии
Пока входные данные соответствуют этой модели, т.е. лежат на этой линии, декодер их точно восстанавливает. Как только их положение меняется, например, 3 и 1, то кодер дает сумму 4 и декодер интерпретирует это значение как 2 и 2. Вот этот момент здесь ключевой: вектор скрытого состояния описывает некую модель представления данных. И чем точнее эта модель описывает входные значения, тем лучше декодер может их восстанавливать. Конечно, НС с линейной функцией активации может формировать модель только в виде линии (одномерный случай) или гиперплоскости (многомерный случай). Но, используя нелинейные активационные функции (сигмоида, ReLu и т.п.) можно сформировать практически любую модель. И эта модель создается в процессе обучения автоэнкодера. Давайте реализуем относительно простой автоэнкодер в виде многосвязной НС для представления изображений цифр из БД MNIST, с которой ранее мы уже работали. На этом примере мы наглядно увидим результат использования сложной нелинейной модели. Вначале импортируем необходимые библиотеки, загружаем цифры из базы MNIST и нормируем их входные значения к диапазону от 0 до 1: import numpy as np import matplotlib.pyplot as plt from tensorflow.keras.datasets import mnist # библиотека базы выборок Mnist from tensorflow import keras from tensorflow.keras.layers import Dense, Flatten, Reshape, Input (x_train, y_train), (x_test, y_test) = mnist.load_data() # стандартизация входных данных x_train = x_train / 255 x_test = x_test / 255 x_train = np.reshape(x_train, (len(x_train), 28, 28, 1)) x_test = np.reshape(x_test, (len(x_test), 28, 28, 1)) Затем, опишем архитектуру нашего автоэнкодера: input_img = Input((28, 28, 1)) x = Flatten()(input_img) x = Dense(128, activation='relu')(x) x = Dense(64, activation='relu')(x) encoded = Dense(49, activation='relu')(x) d = Dense(64, activation='relu')(encoded) d = Dense(28*28, activation='sigmoid')(d) decoded = Reshape((28, 28, 1))(d) autoencoder = keras.Model(input_img, decoded, name="autoencoder") autoencoder.compile(optimizer='adam', loss='mean_squared_error') Здесь у нас вектор скрытого состояния имеет размерность в 49 элементов. Далее, мы обучаем автоэнкодер так, чтобы он как можно точнее восстанавливал входные изображения по вектору скрытого состояния: autoencoder.fit(x_train, x_train, epochs=20, batch_size=batch_size, shuffle=True) Отобразим первые 10 изображений и результат их декодирования нашим обученным автоэнкодером: n = 10 imgs = x_test[:n] decoded_imgs = autoencoder.predict(x_test[:n], batch_size=n) plt.figure(figsize=(2*n, 2*2)) for i in range(n): ax = plt.subplot(2, n, i+1) plt.imshow(imgs[i].squeeze(), cmap='gray') ax.get_xaxis().set_visible(False) ax.get_yaxis().set_visible(False) ax2 = plt.subplot(2, n, i+n+1) plt.imshow(decoded_imgs[i].squeeze(), cmap='gray') ax2.get_xaxis().set_visible(False) ax2.get_yaxis().set_visible(False) На выходе увидим следующее:
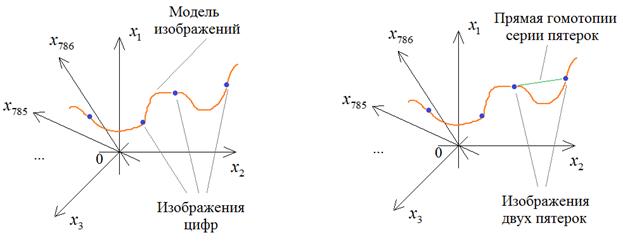
Как видите, результаты получились вполне сносными, с небольшими отличиями, так как вектор скрытого состояния способен удерживать лишь значимые детали входных изображений. Детали получаются расплывчатыми, смазанными. Но что мы в действительности получили? Смотрите, любое изображение размером 28х28 пикселей можно представить как точку в 786-мерном пространстве. Большинство точек этого пространства будут соответствовать шумовым, непонятным изображениям и только малая их часть соответствует цифрам. Кодер в процессе обучения пытается «уловить» область определения этих цифр в этом многомерном пространстве и, в частности, выделяет непрерывную 49-мерную область, в которой находятся образы различных цифр (условно это показано оранжевой кривой на рисунке ниже).
Давайте отобразим цифры, которые получаются гомотопией между двумя изображениями пятерок по прямой. Для этого запишем две вспомогательные функции: def plot_digits(*images): images = [x.squeeze() for x in images] n = min([x.shape[0] for x in images]) plt.figure(figsize=(2*n, 2*len(images))) for j in range(n): for i in range(len(images)): ax = plt.subplot(len(images), n, i*n + j + 1) plt.imshow(images[i][j]) plt.gray() ax.get_xaxis().set_visible(False) ax.get_yaxis().set_visible(False) plt.show() def plot_homotopy(frm, to, n=10, autoencoder=None): z = np.zeros(([n] + list(frm.shape))) for i, t in enumerate(np.linspace(0., 1., n)): z[i] = frm * (1-t) + to * t # Гомотопия по прямой if autoencoder: plot_digits(autoencoder.predict(z, batch_size=n)) else: plot_digits(z) Первая просто отображает набор изображений цифр, а вторая выполняет гомотопию как по прямой, так и по линии сформированной модели. Вызовем функцию plot_homotopy для изображений двух пятерок: frm, to = x_test[y_test == 5][1:3] plot_homotopy(frm, to) plot_homotopy(frm, to, autoencoder=autoencoder) Получим следующий результат:
Смотрите, простое движение по прямой между двумя образами дает нам проявление второй пятерки и плавное затемнение первой. Но когда мы преобразуем эти промежуточные изображения в вектор скрытого состояния (с помощью кодера), то переходим в область найденной модели и затем, декодер, восстанавливает текущий скрытый вектор до полного изображения. В результате, мы двигаемся уже по точкам внутри сформированной модели и серия изображений выглядит уже более естественной. Фактически, здесь мы сгенерировали серию изображений превращения первой пятерки во вторую. Изображения получились не очень хорошие, особенно в средней области. Результат можно постараться улучшить, используя сверточные НС и увеличив размерность вектора скрытого состояния. Но в следующем занятии мы пойдем другим путем и рассмотрим довольно популярную технику компактного представления входных данных в векторе скрытого состояния с помощью вариационного автоэнкодера. Курс по нейронным сетям: https://stepik.org/a/227582 Видео по теме |