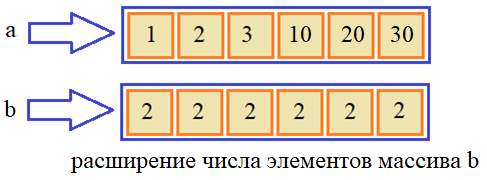
Транслирование массивов

Представьте, что у нас имеются два массива с разным числом элементов:

a = np.array([1, 2, 3, 10, 20, 30])
b = np.array([2])

Можем ли мы выполнять арифметические операции с такими объектами? Оказывается да, можем, например:

a*b # array([ 2,  4,  6, 20, 40, 60])
a+b # array([ 3,  4,  5, 12, 22, 32])

В первом случае каждый элемент массива a будет умножен на первый элемент массива b. А во втором случае выполняется аналогичная операция сложения. Но почему это сработало? Например, если мы в массиве b пропишем два элемента:

b = np.array([2, 3])

и выполним ту же операцию умножения:

a*b # ошибка, размеры не согласованы

возникнет ошибка. Так почему в первом случае это сработало, а во втором – не сработало? Все дело в особенностях работы алгоритма транслирования массивов пакета NumPy, который следует двум правилам:

Если массивы имеют разное число осей (размерностей), то к массиву с меньшим их числом добавляются новые так, чтобы размерности совпадали. (Причем, добавление всегда происходит с оси axis0).
Оси с одним элементом расширяются (по числу элементов) так, чтобы соответствующие размерности двух массивов совпадали.

Чтобы все было понятнее, давайте рассмотрим эти правила на конкретных примерах. Если обратиться к массивам a и b, то число осей у них одинаковое. В этом легко убедиться, выполнив команды:

a.ndim  # 1
b.ndim  # 1

То есть, первый пункт выполняется. И, когда массив b содержал всего один элемент, то согласно второму пункту он мог размножиться до размеров массива a. Получаем равные массивы а, значит, с ними можно выполнять любые математические операции.

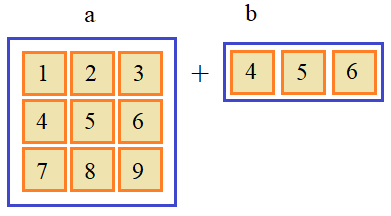
Соответственно, как только в массив b был добавлен еще один второй элемент, то второй пункт не мог быть реализован, и возникла ошибка при вычислении.

Так выполняется транслирование одномерных массивов. Давайте теперь посмотрим, как работает этот механизм с многомерными массивами. Для начала положим, что имеется двумерный и одномерный массивы:

a = np.arange(1, 10).reshape(3,3)
b = np.array([4, 5, 6])

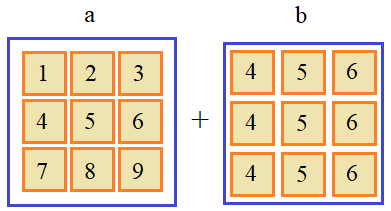
И попробуем их сложить:

a+b # array([[ 5,  7,  9],   [ 8, 10, 12],   [11, 13, 15]])

С точки зрения математики такая операция невозможна. Но в NumPy она легко вычисляется. Как вы догадались, все дело в механизме транслирования. Согласно первому правилу размерность массива b была увеличена до двух, причем, добавлена именно первая ось – axis0:

# a: 3 x 3
# b: 1 x 3

А, затем, по второму правилу, число элементов вдоль оси axis0 массива b было доведено до трех:

Теперь, никаких проблем в сложении данных нет, и получаем искомый результат. Фактически, так работает механизм транслирования массивов при любых размерностях. Ниже я приведу несколько примеров.

Пусть имеются два массива:

a = np.arange(6).reshape(3, 1, 2)
b = np.ones(4).reshape(2, 2)

Тогда, выполняя операцию:

a * b # массив размерностью (3, 2, 2)

Как она была реализована? Смотрите, сначала по первому правилу размерность массива b была доведена до размерности массива a:

# a:  3  x 1 x 2
# b: (1) x 2 x 2

Затем, по второму правилу все оси с одним элементом были расширены до нужного числа элементов. В итоге, были сформированы два массива размерностями:

# a:  3  x (2) x 2
# b: (3) x  2  x 2

После их поэлементного умножения, получаем искомый результат. Как видите, все довольно просто.

Однако, если изменить размерность массива a до 2x3x1:

a = a.reshape(2, 3, 1)

то при математическом действии с массивом b произойдет ошибка:

a * b # ошибка, размеры не согласованы

Почему это произошло? Смотрите, по первому правилу размерности массивов стали равны:

# a:  2  x 3 x 1
# b: (1) x 2 x 2

Соответственно вторая ось у массива a содержит 3 элемента, а у массива b – два элемента. Как мы уже знаем, эти размерности не могут быть приведены друг к другу. Отсюда и возникает ошибка при их умножении. Но, если размерность массива b сделать 3x2:

b = np.ones(6).reshape(3, 2)

то все заработает:

a * b # массив 2x3x2

Вот так происходит транслирование массивов при поэлементных математических операциях.

Функция ix_()

Благодаря механизму транслирования можно выполнять довольно интересные манипуляции с одномерными массивами. Давайте предположим, что у нас есть три массива с разным числом элементов:

a = np.array([1, 2, 3])
b = np.array([4, 5])
c = np.array([7, 8, 9, 10])

И мы собираемся выполнить вот такое вычисление:

a * b + c # ошибка, размеры не согласованы

Разумеется, здесь возникнет ошибка, так как число элементов в массивах разное. Но, мы можем привести их к согласованной форме, добавив по две новой оси в каждый из них. Причем, размерности сделаем следующими:

# a: 1 x 1 x 3
# b: 1 x 2 x 1
# c: 4 x 1 x 1

Как вы теперь знаете, с такими массивами можно выполнять любые поэлементные операции. Поменяем размерности:

a.shape = 1, 1, -1
b.shape = 1, -1, 1
c.shape = -1, 1, 1

И теперь, можем спокойно выполнить искомое действие:

a * b + c # массив 4x2x3

Фактически, мы здесь получили все возможные варианты перемножений вектора a на числа 4 и 5 и сложений с числами 7, 8, 9 и 10. Для этого было достаточно к одномерным массивам добавить соответствующие оси. Так вот, эту операцию можно автоматизировать с помощью функции ix_(), следующим образом:

a = np.array([1, 2, 3])
b = np.array([4, 5])
c = np.array([7, 8, 9, 10])
an, bn, cn = np.ix_(a, b, c)

На выходе имеем массивы an, bn и cn с нужным расположением и числом осей. И, далее, осталось только выполнить математическое действие:

an * bn + cn # массив 3x2x4

Единственным ограничением этой функции является ее применимость только к одномерным массивам. С многомерными она не работает и приводит к ошибке.

Транслирование массивов

Функция ix_()

Видео по теме