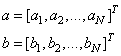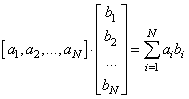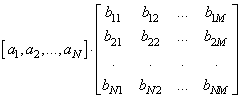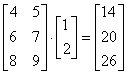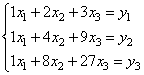|
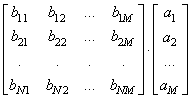
Произведение матриц и векторов, элементы линейной алгебрыПришло время познакомиться с одной из фундаментальных возможностей пакета NumPy–матричных и векторных вычислений. На одном из прошлых занятий мы с вами уже видели, как можно поэлементно умножать один вектор на другой или одну матрицу на другую: a = np.arange(1, 10).reshape(3, 3) b = np.arange(10, 19).reshape(3, 3) a*b В консоли увидим результат: array([[
10, 22, 36],
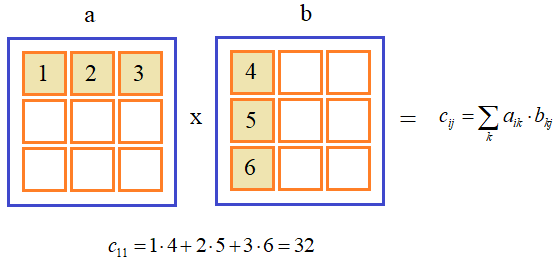
Матричное умножениеНо если нам нужно выполнить именно матричное умножение, то есть, строки одной матрицы умножать на столбцы другой и результаты складывать:
то для этого следует использовать специальные функции и операторы. Начнем с функций. Итак, чтобы перемножить две матрицы a иbпо всем правилам математики, запишем следующую команду: np.dot(a, b) Эта функция возвращает новую матрицу (двумерный массив) с результатом умножения: array([[ 84, 90, 96],
Тот же результат можно получить и с помощью функции: np.matmul(a, b) Считается, что этот вариант предпочтительнее использовать при умножении матриц. Векторное умножениеАналогичные операции можно выполнять и с векторами. Математически, если у нас имеются два вектора:
то их умножение можно реализовать в двух видах:
и
Первое умножение реализуется либо через функцию: a = np.arange(1, 10) b = np.ones(9) np.dot(a, b) # значение 45 Либо, более предпочтительной функцией для внутреннего умножения векторов: np.inner(a, b) # 45 Второй вариант умножения (внешнее умножение векторов) реализуется с помощью функции: np.outer(a, b) получим результат в виде следующей матрицы: array([[1.,
1., 1., 1., 1., 1., 1., 1., 1.],
Операция умножения матриц и векторов используется довольно часто, поэтому в пакете NumPy имеется весьма полезный перегруженный оператор, заменяющий функцию matmul: a @ b # значение 45 или, с использованием матриц: a.resize(3, 3) b.resize(3, 3) a @ b # аналог np.matmul(a, b) Умножение вектора на матрицуНаконец, рассмотрим умножение вектора на матрицу. Это также можно записать двумя способами:
или
Для реализации первого способа, зададим одномерный вектор и двумерную матрицу: a = np.array([1,2,3]) b = np.arange(4,10).reshape(3,2) # матрица 3x2 И, затем, воспользуемся уже знакомой нам функцией dot: np.dot(a, b) # array([40, 46]) При такой записи, когда одномерный массив записан первым аргументом, а матрица – вторым, получаем умножение вектора-строки на матрицу, то есть, первый способ. Для реализации второго способа аргументы нужно поменять местами: сначала указать матрицу, а затем, вектор. Но, если мы сейчас это сделаем с нашими массивами, то получим ошибку: np.dot(b, a) # несогласованность размеров Дело в том, что массив a должен представлять вектор длиной два элемента, так как матрица b имеет размер в 3 строки и 2 столбца:
Определим массивa в два элемента и умножим на матрицу b: a = np.array([1, 2]) np.dot(b, a) # array([14, 20, 26]) Получаем вектор-строку (одномерный массив) как результат умножения. Обратите внимание, по правилам математики вектор aдолжен быть вектором-столбцом, то есть, быть представленным в виде: a.shape = -1, 1 # вектор-столбец 2x1 Но мы использовали вектор-строку. В NumPyтак тоже можно делать и это не приведет к ошибке. Результат будет именно умножение матрицы как бы на вектор-столбец. Ну а если использовать вектор-столбец, то и на выходе получим вектор-столбец: np.dot(b, a) # вектор-столбец 3x1 Этого же результат можно достичь, используя оператор @ (перегрузка функции matmul): a @ b # вектор-столбец 3x1 Результат будет тем же. Вот так в NumPyвыполняется умножение матриц, векторов и вектора на матрицу. Элементы линейной алгебрыИз высшей математики хорошо известно, что матрицы можно использовать для решения систем линейных уравнений. Для этого в NumPyсуществует модуль linalg. Давайте рассмотрим некоторые из его функций. Предположим, имеется квадратная матрица 3x3: a = np.array([(1, 2, 3), (1, 4, 9), (1, 8, 27)]) Первым делом вычислим ранг этой матрицы, чтобы быть уверенным, что она состоит из линейно независимых строк и столбцов: np.linalg.matrix_rank(a) # рангравен 3 Если ранг матрицы совпадает с ее размерностью, значит, она способна описывать систему из трех независимых линейных уравнений. В нашем случае, система уравнений будет иметь вид:
Здесь y = np.array([10, 20, 30]) Тогда корни уравнения можно вычислить с помощью функции solve: np.linalg.solve(a, y) # array([-5. , 10. , -1.66666667]) Другой способ решения этой же системы линейных уравнений возможен через вычисление обратной матрицы. Изначально, уравнение можно записать в векторно-матричном виде:
Откуда получаем
решения
На уровне пакета NumPy это делается так: invA = np.linalg.inv(a) # вычисление обратной матрицы invA @ y # вычисление корней Конечно, я здесь представил лишь примеры использования модуля linalg. Приводить все функции нет смысла, так как они имеют довольно специализированное назначение и специалисты в своих областях без труда смогут ими воспользоваться. Для полноты картины я лишь приведу список наиболее характерных функций, чтобы вы знали возможности расширения linalg.
Конечно, это не все математические функции пакета NumPy. Полное описание смотрите на сайте с официальной документацией: Видео по теме |